C++栈的应用：逆波兰式的实现

Posted 2021-12-19 蓝乐

逆波兰表达式

• 一.定义
• 二.逆波兰式的意义
• 三.逆波兰式的实现
• • 1.方法
  • • （1）中缀表达式转化为后缀表达式
    • （2）由后缀表达式计算结果
  • 2.代码实现

一.定义

逆波兰式，又称后缀表达式，指的是操作符在其所控制的操作数后面的表达式。
举个例子，1 + 2 * 3 - 4这个表达式是我们熟悉的中缀表达式，那么其所对应的后缀表达式为：1 2 3 * + 4 -。
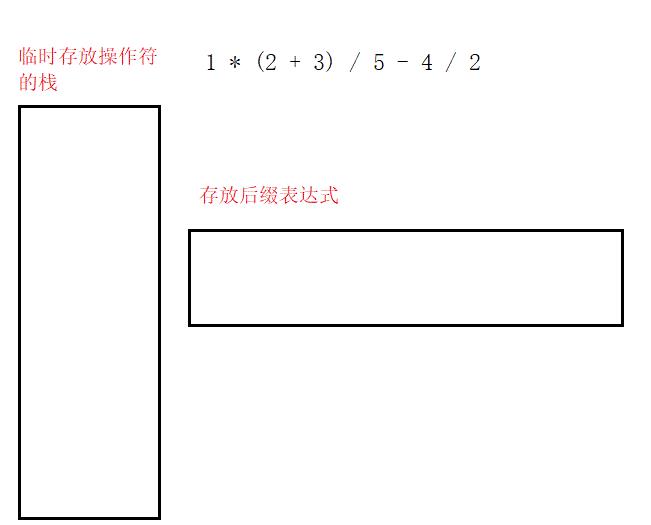
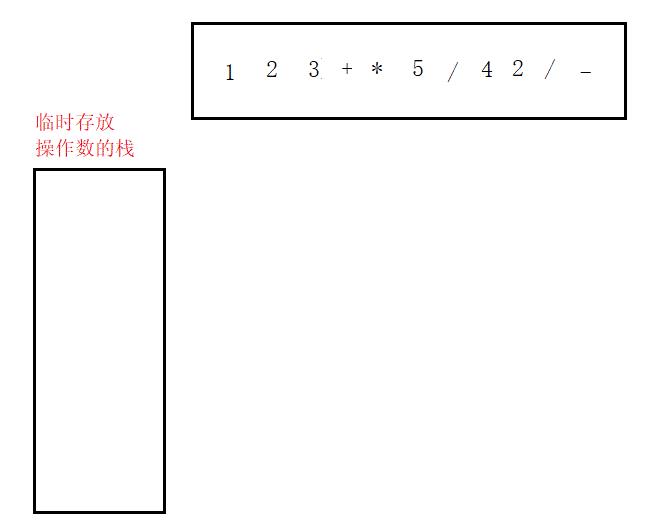
再来个复杂的例子：1 * (2 + 3) / 5 - 4 / 2其对应的后缀表达式为：1 2 3 + * 5 / 4 2 / -（其中括号由于只是提升表达式优先级的作用，因此不放入后缀表达式中）。

二.逆波兰式的意义

为什么要将看似简单的中缀表达式转换为复杂的逆波兰式，原因就在于这个简单是相对我们人类的思维结构来说的，对计算机而言中序表达式是非常复杂的结构。相对的，逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构，它执行先进后出的顺序。

三.逆波兰式的实现

1.方法

（1）中缀表达式转化为后缀表达式

对于给出的中缀表达式，如何将其转化为后缀表达式呢？
第一，若遇到操作数则直接输出/存储。
第二，遇到操作符，若此时栈为空或者操作符优先级高于栈顶，则入栈。
第三，若操作符的优先级低于或者等于栈顶，则出栈直至栈空或者优先级低于该操作符。
第四，遇到’(’,其后的所有操作符（直至遇到’)’）按上述操作入栈或出栈；当遇到’)‘时，将’('顶上的所有操作符出栈。

（2）由后缀表达式计算结果

第一，遇到操作数则入栈。
第二，遇到操作符则将栈顶的两个操作数出栈，其中第一个数为右操作数，第二个数为左操作数。
第三，计算结果并将计算的结果入栈。
第四，最后栈顶的结果即为所计算的结果。

2.代码实现

#include <iostream>
#include <string>
#include <stack>
#include <vector>
using namespace std;

string trans(string& s)

	string operand;
	stack<char> Operator;
	int flag = 0;//记录括号优先级
	for (const auto& e : s)
	
		if (e == '(')
		
			Operator.push(e);
			flag = 1;
			continue;
		
		if (e == ')')
		
			flag = 0;
			while (Operator.top() != '(')
			
				operand.push_back(Operator.top());
				Operator.pop();
			
			Operator.pop();
			continue;
		
		//操作符
		if (e == '+' || e == '-' || e == '*' || e == '/')
		
			if (flag == 1)
			
				if (Operator.top() == '(')
				
					Operator.push(e);

				
				else if ((e == '*' || e == '/') && (Operator.top() == '+' || Operator.top() == '-'))
				
					Operator.push(e);
				
				else//操作符的优先级低于或等于栈顶操作符则出栈，直至遇到'('
				
					while (Operator.top() != '(')
					
						operand.push_back(Operator.top());
						Operator.pop();
					
					Operator.push(e);
				
			
			else if (Operator.empty())//栈空就入栈
			
				Operator.push(e);
			
			//操作符的优先级高于栈顶操作符，入栈
			else if ((e == '*' || e == '/') && (Operator.top() == '+' || Operator.top() == '-'))
			
				Operator.push(e);
			
			else//操作符的优先级低于或等于栈顶操作符则出栈，直至栈空或者优先级高于栈顶操作符
			
				while (!Operator.empty())
				
					operand.push_back(Operator.top());
					Operator.pop();
				
				Operator.push(e);
			
		
		//操作数
		else
		
			operand.push_back(e);
		
	
	while (!Operator.empty())
	
		operand.push_back(Operator.top());
		Operator.pop();
	
	return operand;


int evalRPN(const string& s)

	stack<char> operand;
	int left = 0, right = 0;
	for (const auto& e : s)
	
		if (e == '+' || e == '-' || e == '*' || e == '/')
		
			switch (e)
			
			case '+':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left + right);
				break;
			case '-':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left - right);
				break;
			case '*':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left * right);
				break;
			case '/':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left / right);
				break;
			
		
		else//操作数
		
			operand.push(e - '0');
		
	
	return operand.top();


int RPN(const string& str)

	//1.中缀表达式转化为后缀表达式
	string s(str);
	s = trans(s);
	//2.后缀表达式计算答案
	return evalRPN(s);


int main()

	string s("1*(2*3+5)/5-4/2");
	int ret = RPN(s);
	cout << "ret:" << ret << endl;
	return 0;

结果: