深度学习入门与实战- 卷积神经网络

Posted 2021-12-19 gonghaiyu

上一讲我说到了线性回归模型，它可以帮助我们解决房价预测等回归、拟合的问题，我们也可以对回归方程 f(x)输出加一个 Sigmoid 函数，使其也能应用在分类问题上。

但现实中除了分类问题还有很多不同的场景，会用到图像算法、文本算法、音视频算法等等。今天，就让我来带你学习卷积神经网络（Convolutional Neural Networks，CNN）在图像，音频上的应用。

卷积神经网络在人脸识别、智慧医疗、工业检测等方面有着广泛的应用，极大地缩减了人力物力的投入，并有着比人类更高效精确的表现。

接下来，为帮助你更好地理解卷积神经网络，我们先来看几个与之相关的概念，它们分别是卷积、激活函数、池化和感受野。

卷积

卷积在卷积神经网络中的主要作用是提取图片的特征，同时保留原来图片中各个像素的相对位置（空间）关系。举个例子，假设我们有 1 个 5x5 的矩阵 A 和 1 个 3x3 的矩阵 B，我们将这两个矩阵进行卷积操作（这有点类似点乘计算），操作过程如下图：

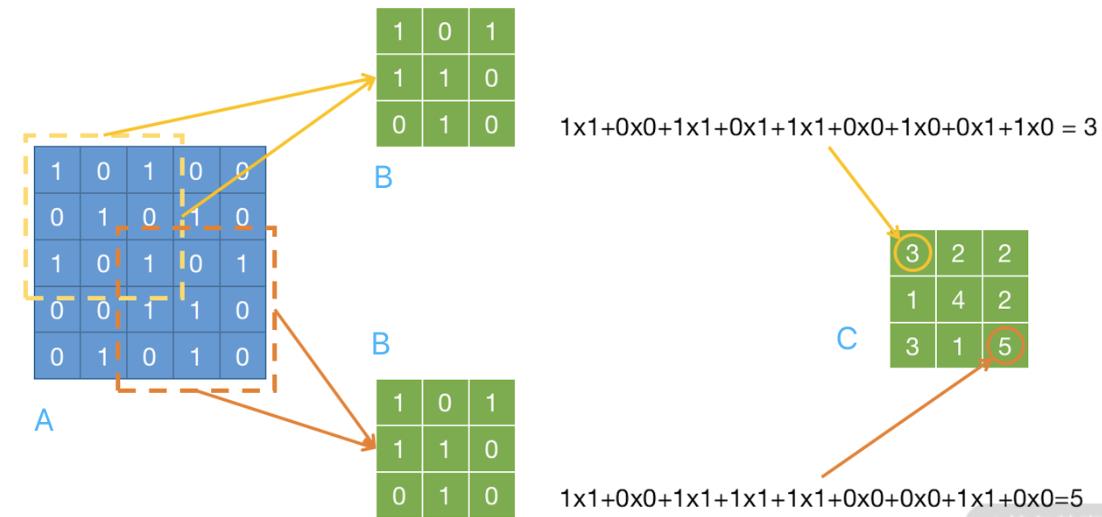
在这个过程中总共出现了 3 种矩阵：

1. 原始图像的矩阵（A），这个实际上就是我们眼睛看到的世界。
2. 3x3 矩阵（B），我们称为滤波器（Filter）、核（Kernel），或是特征提取器、卷积核。通过对滤波器矩阵设置不同的值，可以实现如边缘检测、锐化以及模糊操作等不同的操作。在实际的模型设计中，我们会使用不同尺寸的滤波器来实现不同的效果。通常我们只需要设定滤波器的尺寸和数量，卷积神经网络就可以自己通过梯度更新或反向传播得到内部的数值。使用越多的滤波器，可以提取到越多的图像特征，神经网络也有更好的性能。
3. 卷积之后得到的矩阵（C），我们称为特征图（Feature Map、 Activation Map）。

如下图 4，原始图片是一张小动物，通过不断变化卷积核的内容，就可以得到不同的结果，有的是轮廓信息（第 2、3、4 行），有的是更加锐化后的信息（第 5 行），有的会变得模糊（第 6、7 行）。

讲解了卷积之后，我需要补充两个知识点：边缘填充和特征图尺寸的计算。

图 3 的计算当中，我们实际上是将滤波器和图像进行了对齐：第一步，滤波器（黄色虚线框）的第 1 个像素和图像的第 1 个像素是重叠的；最后一步，滤波器（棕色虚线框）的最后 1 个像素和图像的最后 1 个像素也是重叠的，这意味着滤波器没有超出图像。

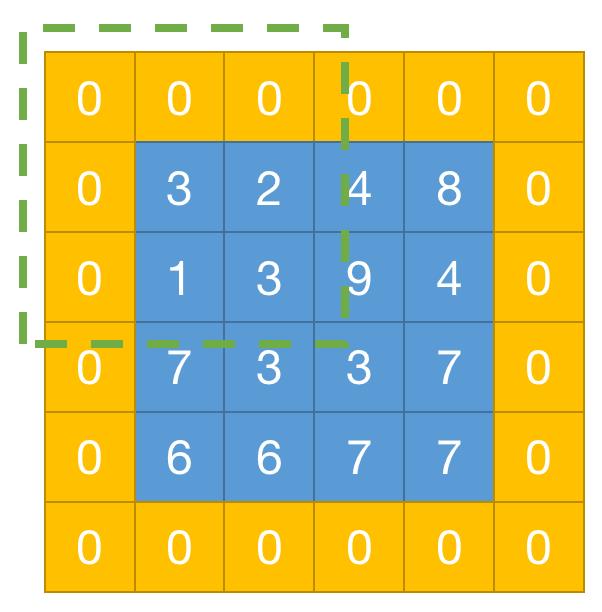
如果我们在输入图像的周围填充一些 0，再把滤波器应用到这些边缘的点上，让滤波器“超出来”一些，这就叫作边缘填充。如下图，蓝色的矩阵是原始图像，外面一圈黄色的 0 就是边缘填充的值，虚线框内是卷积核。通过边缘填充，我们可以控制输出的特征图的大小。

既然说到了特征图的大小，那特征图的大小又跟哪些方面有关呢？这就是我接下来要补充的。

特征图尺寸的计算。假定：O=输出图像的尺寸，I=输入图像的尺寸，K=卷积层的核尺寸，S=移动步长，P=填充数。那么，输出图像尺寸的计算公式即为：O=(I-K+2P)/S+1。

以图 5 为例，I=4，K=3，P=1，S=1（假设我们每次移动 1 格），则输出尺寸 O=(4-3+2x1)/1+1=4。

这个公式非常重要。在设计神经网络结构的时候，神经网络的每一层都是由上一层得到的，只有确保每个层的尺寸无误才能保证神经网络的正常运转。

至此，你对卷积神经网络最基本的运算过程就有了一个大致的了解。接下来，我会介绍卷积神经网络中的另一个概念，激活函数。

激活函数

假设我们有一个简单的神经网络，如图：

这是一个 2 层的网络，其中 X1、X2 是输入，b1、b2 和 b3 是中间层的神经元，第一层是 b1 和 b2，第二层是 b3，Y 是输出。连接线的多个 w 值，对应神经元的权重。其中：

b1 的输出 = w11X1 + w21X2 + b1

b2 的输出 = w12X1 + w22X2 + b2

b3 的输出 Y = w13b1 + w23b2 + b3

=w13*(w11X1 + w21X2 + b1) + w23(w12X1 + w22*X2 + b2) + b3

=(w11w13 + w12w23)X1 + (w21w13 + w22w23)X2 + (b1w13 + b2w23 + b3)

这意味着，X1、X2 前面的系数仍然是一个常数，那么整个网络的输出就可以用 Y=X1Wa + X2Wb + B 来表示，折腾了一顿最后还是一个线性函数。这就相当于做了无用功，一层就能做到的事情，我用了好多层来做。

如果你有一个很大的网络，但是网络内部全都是线性单元，那这个网络一定可以被某种线性组合表示，你的隐藏层（如图 6 中的 b1、b2）就一点作用没有。所以，我们需要在网络中增加非线性函数，即激活函数（也称激励函数），以便让模型有更好的学习能力，或者说更好的特征提取和组合能力，毕竟这个世界有很多问题如天气预测、人脸识别，都是线性模型无法搞定的。

激活函数的种类非常多，常见的一般有：Sigmoid、tanh、ReLU 和Leaky ReLU。
先来看Sigmoid 函数。

在信息科学中，由于其单增以及反函数单增等性质，Sigmoid 函数常被用作神经网络的激活函数。它可以把输入的数值约束到 0~1 的范围内，无论是多大或者是多小的数，都可以使其无限逼近于 0 或 1。如下图：

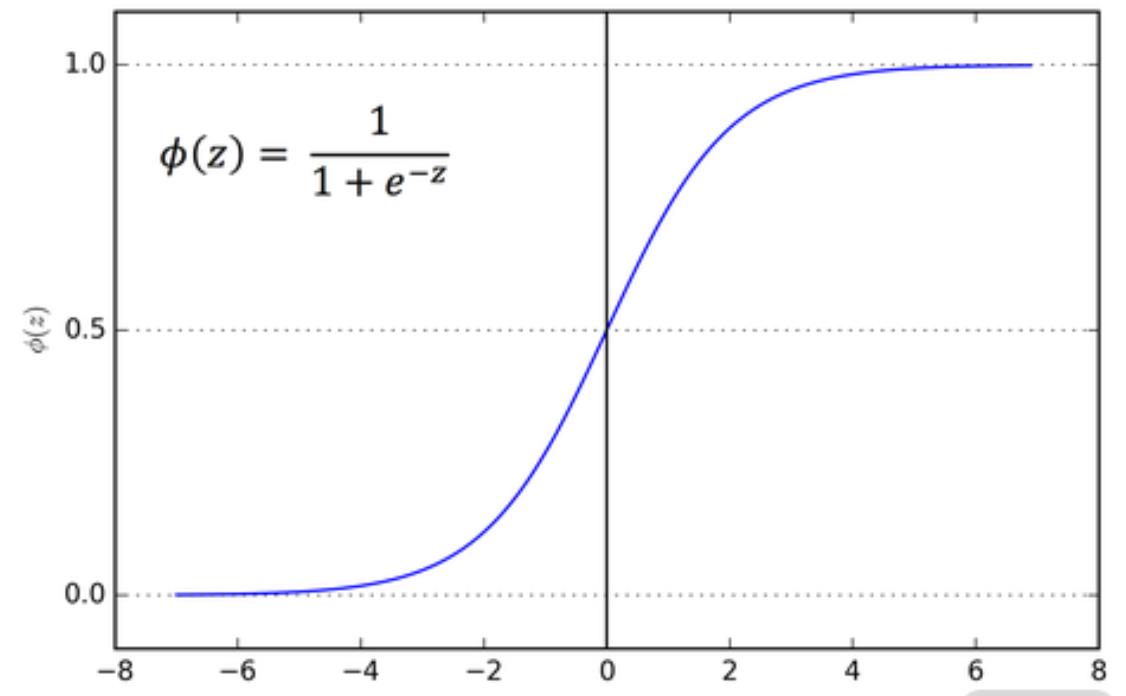
不过，现在 Sigmoid 的使用率在逐渐减少，还记得之前课程中咱们提到过的梯度消失和爆炸问题吗？Sigmoid 的导数是一个驼峰状的函数，取值范围在 0~0.25 之间，当网络层数比较多的时候，多个接近于 0 的数相乘，最后的值就趋近于 0，所以它比较容易引发梯度消失问题，最终导致模型无法正常学习。此外，Sigmoid 函数含有幂运算，在大型网络中幂运算是非常消耗时间的。

我们再来看tanh 函数。

tanh 是双曲函数中的一个，为双曲正切。在数学中，双曲正切“tanh”是由双曲正弦和双曲余弦这两种基本双曲函数推导而来的。tanh 函数也是一个较为常用的激活函数，其公式与图像如下所示：

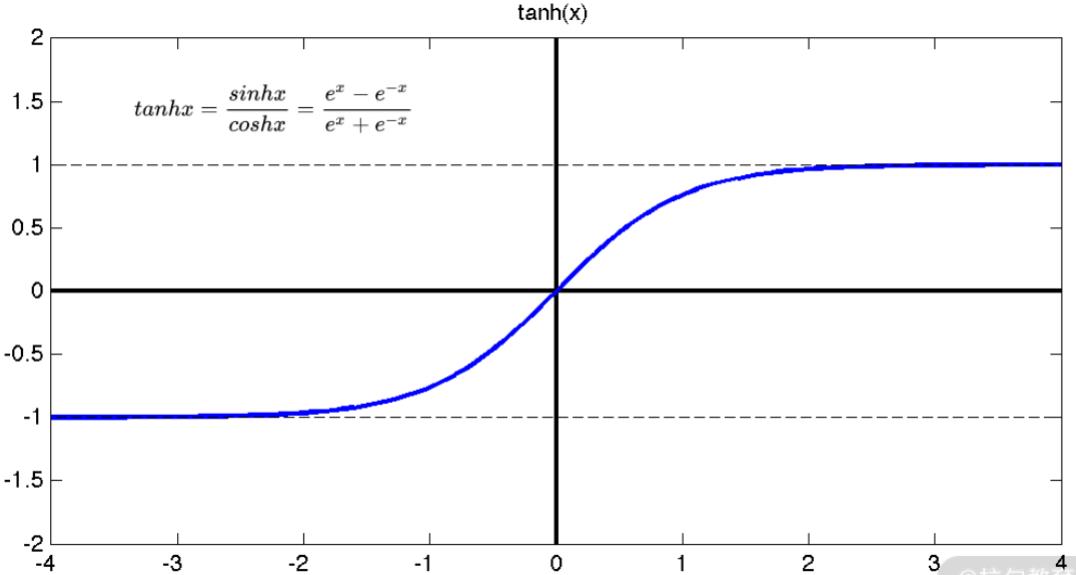
可以看到，跟 Sigmoid 一样，tanh 函数求导之后的值域仍然在 0～1 之间，所以它也没有解决梯度和幂运算计算量大的问题。

接下来是ReLU 函数。

ReLU 函数又称修正线性单元，是一种人工神经网络中常用的激活函数。ReLU 的公式非常简单：Relu=max(0,x)。从图可以看到，当 x≤0 的时候，函数等于 0，而 x＞0 的时候，函数的值就是 x。

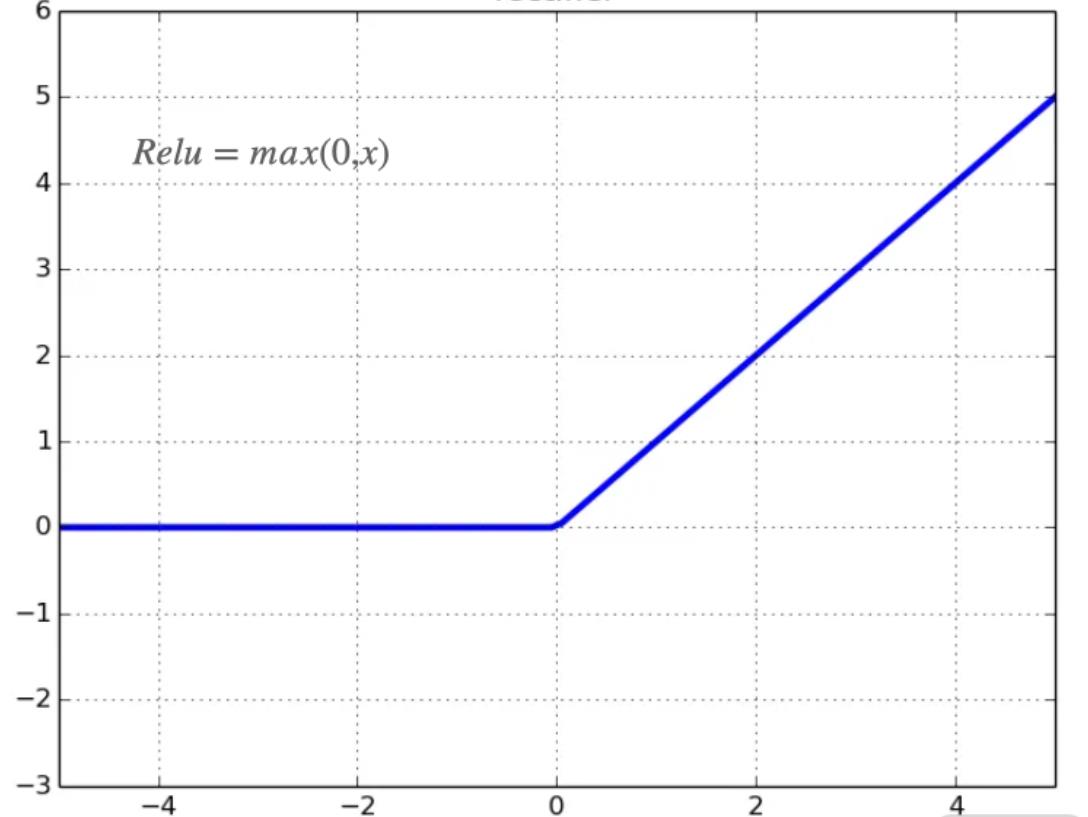
ReLU 函数看似很简单，但简单并不意味着不好用。

当输入＜0 时，ReLU 函数的输出始终等于 0，因此函数的变化率为 0；当输入≥0 时，输出就是输入，因此，它的导数等于 1。

从对 ReLU 函数的描述可以看到，ReLU 函数不仅很大程度上解决了梯度消失的问题，还有着非常快的计算速度，因为它只需要判断是否大于 0 就行了。

当然，它也不是完美的，“ReLU 死区”就是一个很常见的问题，即：在训练一段时间以后，如果某个神经元在某次权重更新之后为负数，那它的激活函数就只会输出 0，这意味着这个神经元“死”掉了，以后再也不会输出其他的值了。例如，在一些特殊的情况下，比如学习率太大，就很容易导致更新后权值为负，从而引发神经元的“死亡”。

最后是Leaky ReLU 函数。

为了解决 ReLU 的致命缺点，脱胎于 ReLU 的 Leaky ReLU 函数应运而生，它的公式是f(x)=max(αx,x)。如下图：

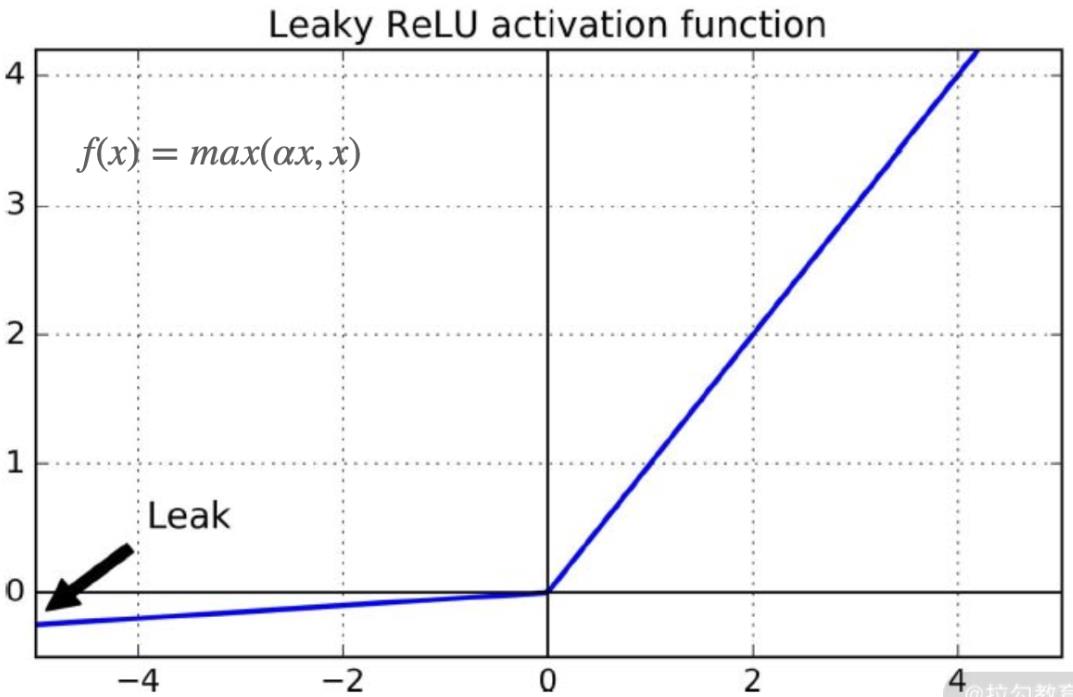
α 是一个超参数，定义了 x<0 时的斜率，比如 0.01。这个小的斜率可以保证激活函数不会出现神经元“死亡”的情况。

池化

卷积操作之后，图片被转化成一张张特征图，数据量有时会很大，所以我们需要一种方式来尽可能地减少计算。于是便有了池化（Pooling）。池化实际上是一种降采样的形式，在尽量保留特征的同时，不断减少数据大小，从而减少参数量和计算量，比如我们压缩 1 张照片，照片大小被压缩后，其中的信息通常不会损失太多。

较为常见的池化有两种：最大池化（Max Pooling）和平均池化（Average Pooling）。

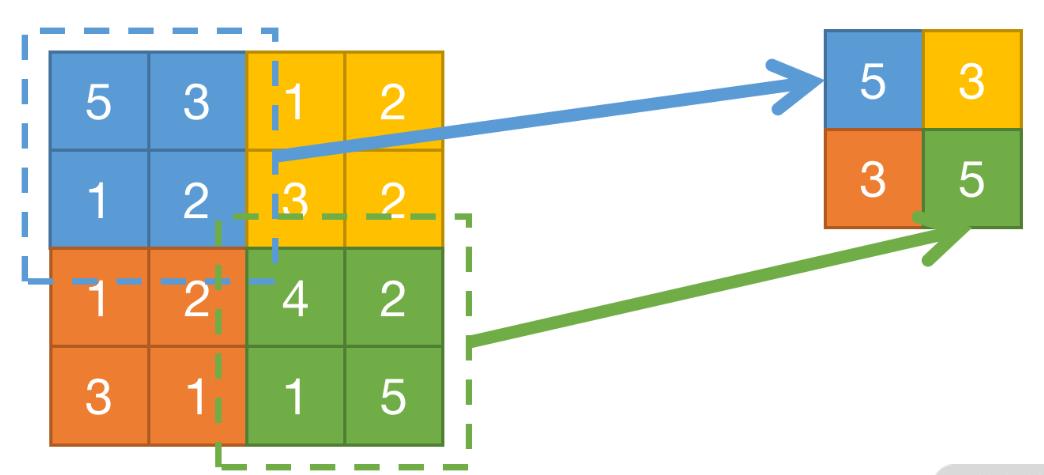
最大池化，顾名思义，就是在一张图内，选择一个池化尺寸，然后选择该尺寸中数值最大的像素点，添进新的特征图，直到该行为覆盖了整张图片。最大池化保留了数据内响应最大也是最强烈的值，相当于保留了照片中最重要的像素点，因此可以在减少计算的同时保留特征。

例如下图，选择池化尺寸为 2x2，在其中分别选出最大值，通过对 4 块区域的最大池化，最终构成了右边新的特征图。

平均池化，也叫均值池化，它是把特征图一个区域内的全部数值取平均值的池化方法。在操作上与最大池化相似，只不过最大池化是取最大值，而平均池化是取区域内数值和的平均数。

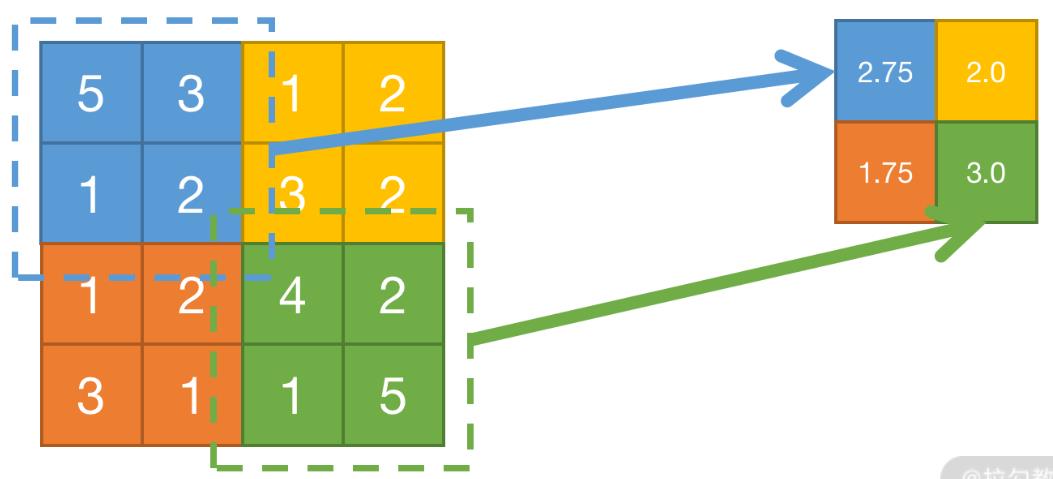
池化之后，新生成的特征图的尺寸会发生变化，假设 I=输入图像的尺寸，F=卷积层的核尺寸，S=移动步长，则输出尺寸 O=(I-F)/S+1。

以上图为例：I=4，F=2，虚线框处理完蓝色的部分后，会往右挪动 2 格，处理黄色的部分，因此 S=2，则 O=(4-2)/2 + 1=2。

在实际使用过程中，两种池化有不同的侧重点。最大池化因为提取的是区域内的特征最强烈的像素，所以一般在网络的前几层使用，用来保留图像的纹理信息，但走到深层的网络之后，特征图的尺寸越来越小，包含的语义信息逐渐增多，最大池化能够获取的信息就会减少。此时，平均池化的优势就显现出来了，在深层的网络中，它依然能够很好地保留背景和语义信息。

感受野

在卷积神经网络中，感受野（Receptive Field）是指卷积神经网络每一层输出的特征图上的像素点在输入图片上映射的区域大小，也就是特征图上的一个点对应输入图上的区域。感受野跟步长、卷积核尺寸有关，计算公式如下：

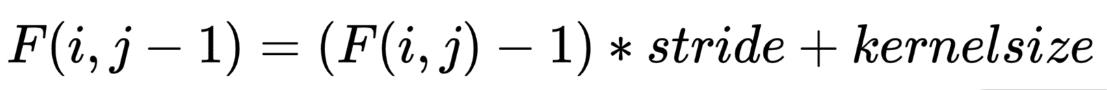
其中F(i, j)表示第 i 层对第 j 层的局部感受野， stride为卷积核移动步长，kernelsize为卷积核尺寸。

通过公式，你可以将感受野简单地理解为像素能够感应的范围大小。在后续的学习中，我们还会多次遇到它，希望你能够记住它的定义。

卷积神经网络

我们回忆一下之前提起的神经网络模型。当网络输入一个数据之后，中间要经过若干个隐藏层，如果每一个隐藏层中的每一个神经元都跟前一层的神经元相连，会产生巨大的计算量。

举个例子，在一个如图 13 的全连接网络中，m-1 层有 1000 个神经元，m 层有 1000 个神经元，那么两层之间的全连接（图中蓝色的线）的数量就是 1000x1000=100 万个，如果神经网络有更多层，那连接的数量会变得更加庞大。

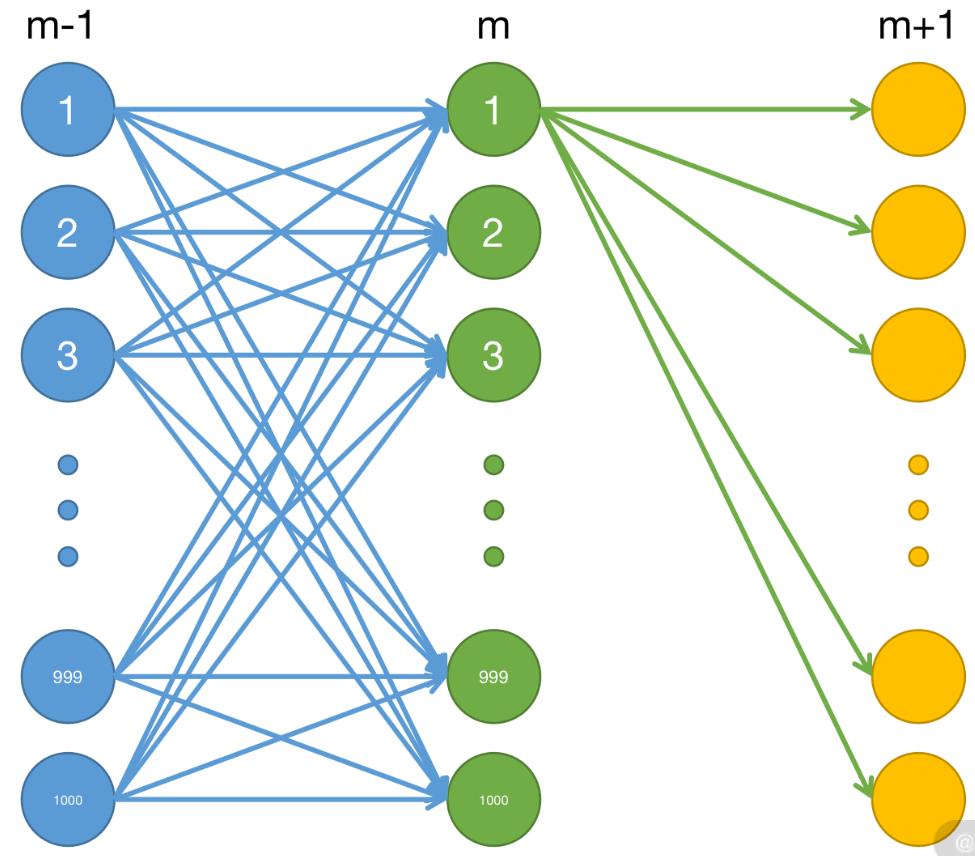
那有什么办法可以让连接的数量不那么多呢？

我们可以把 m 层中的每个节点都限定一下连接数量，比如每个节点只跟 10 个 m-1 层的神经元连接，如下图（图中只画出 3 个），这样一来，连接的数量就从 1 百万个变成了 10x1000=1 万个，减少了 100 倍。这个操作，就叫作稀疏连接（Sparse Connectivity），也叫参数减少。

现在 m 层的每个神经元连接的区域是 10 个神经元，如果我们把 m 层修改一下，改为只有相同的 10 个神经元的集合 F，然后用集合 F 不断地与 m-1 层的 10 个神经元连接，如下图所示：

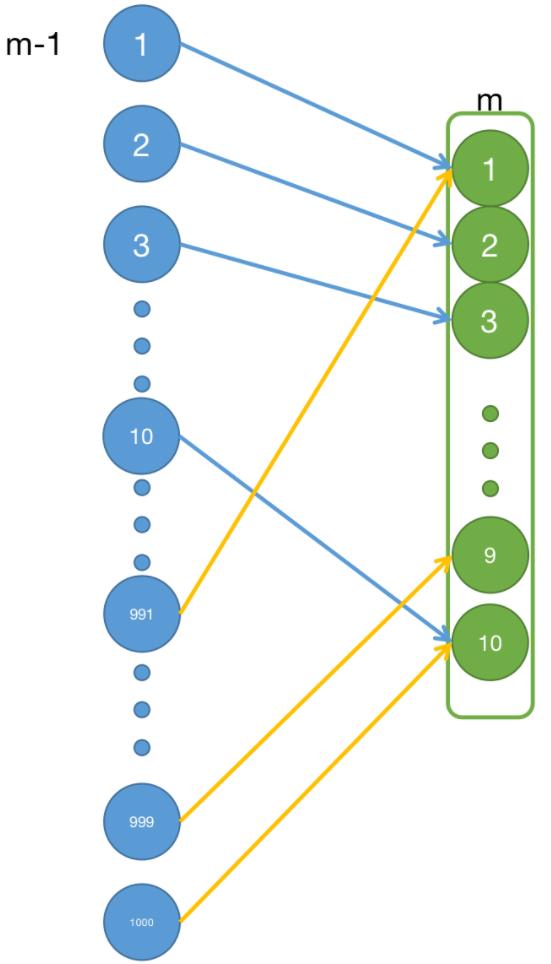
集合 F 对应的操作，叫作权值共享，F 就是权值。换句话说就是每一次的连接都是用相同的权值，共享使用。你看，通过权值共享，连接的数量是不是又进一步减少了？

参数减少、权值共享是卷积神经网络最大的两个特点。

这时候你可能会有疑问，这个跟前面说的卷积计算方法为什么不太一样？

我们把 m-1 层的“一长条”神经元，变为方形或者矩形的像素矩阵，再把集合 F 也变成类似的方形矩阵，m-1 层就成了图片，集合 F 就成了卷积核（图 3），这就变成了卷积操作构成的网络，即卷积神经网络。

了解完卷积神经网络的概念和特点，我们就可以开始组装一个卷积神经网络了。在组装的过程中，你也能够更直观地了解卷积神经网络的构造和样式。

我们现在回顾一下，手头有什么可以用的零件：

1. 卷积核：提取特征。
2. 池化：减少参数和计算量。
3. 全连接层：分类。
4. 激活函数：表示更加复杂的学习过程。

活用它们，我们就能用卷积神经网络来做一个简单的分类网络了。

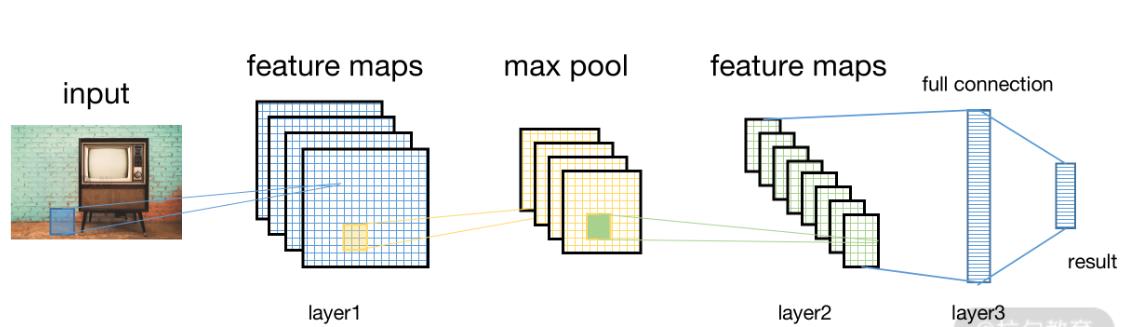
恰好我们手上有一张图片，我们先用若干个卷积核提取图片的特征（如刚才所说，不同的卷积核可以提取到图片不同的特征信息）。

经过卷积操作后，我们在特征图上加一个激活函数。如下图所示，我们提取了第一层的特征。

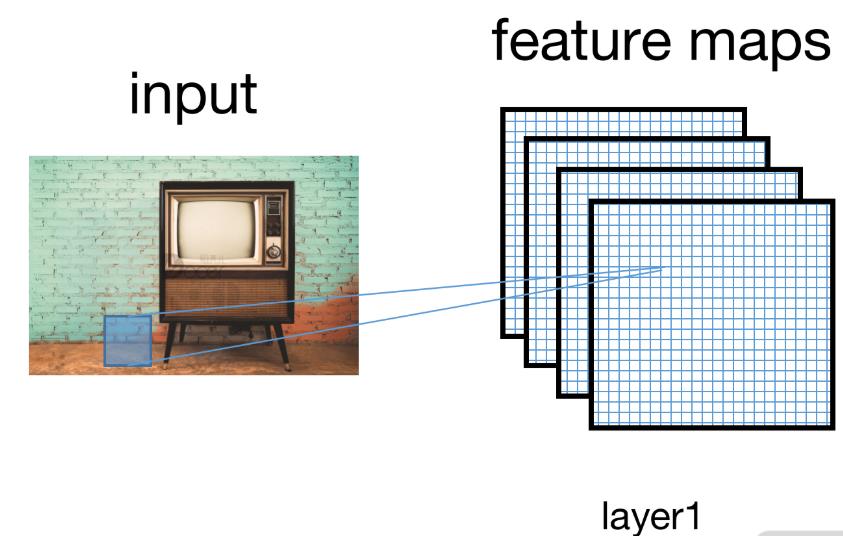
经过这一系列操作后，我们就有了很多提取出来的特征图。下一步，我们要对这些特征图变形，让它们变成向量的形式，这可以方便我们增加一层全连接层，从而将分类的结果映射到不同的类别上。如下图所示：