数据结构之栈和队列熬夜暴肝，有亿点详细

Posted 2021-12-19 _白白不白

前言

我们之前已经说过线性表那一部分了，今天正式开始栈与队列这部分。这部分用途是十分的广泛，重要程度也是不言而喻的。大家理解性记忆哈，多练习！

栈的很多东西与线性表类似，大家对线性表有什么不了解的可以先去看看我上次写的线性表相信对你能有帮助。

传送门->数据结构之线性表

目录

• 前言
• 栈
• • 栈的定义
  • 顺序栈
  • 链栈
• 队列
• • 队列的定义
  • 顺序队列
  • • 循环队列
  • 链式队列
• 栈与队列的应用
• • 双端队列
  • 栈的应用
  • • 表达式求值
    • 括号匹配
    • 递归
• 结语

栈

栈其实就是受限制的线性表，线性表有两种，所以栈按照存储结构来分也有两种。

栈的定义

栈(Stack）：只允许在一端进行插入或删除的线性表

栈有两个概念是：栈底和栈顶。一般栈只允许在栈顶进行操作，这样就会让栈有一个特性：后进先出（LIFO）。
栈的基本操作

InitStack(&S)：初始化一个空栈S。

StackEmpty(S)：判断一个栈是否为空，若栈为空则返回true，否则返回false。

Push(&S, x)：进栈，若栈S未满，则将x加入使之成为新栈顶。

Pop(&S, &x)：出栈，若栈非空，则弹出栈顶元素，并用x返回。

GetTop(S, &x)：读栈顶元素，若栈非空则用x返回栈顶元素。

ClearStack(&S)：销毁栈，并释放S占用的内存空间

栈有两种分别是：顺序栈和链栈，接下来我们将它们逐个击破。

顺序栈

顺序栈顾名思义就是采用顺序存储结构的栈

顺序栈的定义为

# define MaxSize 50
typedef struct
	ElemType date[MaxSize];
	//top用来存放栈顶位置
	int top;
SqStack;

栈的一些常用条件

判断栈空：S.top==-1

求栈长：S.top+1

栈满条件：S.top==MaxSize-1

栈的初始化也是非常特殊的，也非常简单,只需要将栈顶位置初始化为-1即可，如下：

void TnitStack (SqStack &S)
	S.top=-1;

判断栈空

bool StackEmpty(SqStack S)
	if(S.top==-1)
		return true;
	else
		return false;

进栈操作

进栈之前先判断栈是否满了。没有满可以继续存放数据，进栈成功之后返回true。

bool Push(SqStack &S,ElemType x)
	if(S.top==MaxSize-1)
		return false;
	S.date[++S.top]=x;
		return true;

出栈操作

出栈之前判断栈中有无元素，没有则不能进行出栈操作，并返回false。

bool Pop(SqStack &s,ElemType &x)
	if(S.top==-1)
		return false;
	x=S.date[S.top--];
		return true;

与出栈类似的就是获取栈顶元素，这时候不需要对栈进行改变所以不需要传入栈的引用了，如下：

bool Pop(SqStack S,ElemType &x)
	if(S.top==-1)
		return false;
	x=S.date[S.top];
		return true;

共享栈

共享栈就是两个栈公用同一块顺序内存，将两个栈底设置在共享空间的两端，栈顶向空间中间延伸

共享栈与普通栈不同之处就只有判断栈空栈满的条件和栈顶的移动方向，如下：

判空：内存底部栈 top == -1
内存顶部栈 top == MaxSize

栈满：top1-top0 == 1

共享栈的优点是：存取时间复杂度仍为O(1)，但空间利用更加有效

其实所谓的进栈出栈，原来的元素还在存储空间上，只不过，每次都是把他们覆盖了而已，我们只通过栈顶位置来判断，来限制定义操作这个栈，可见栈顶（top）移动的重要性。

链栈

链栈就是采用链式存储的栈，有栈顶结点与栈低结点

链栈的定义

链栈的定义与链表定义几乎相同，它们唯一的不同之处就是在操作上了

typedef struct Linknode
	ElemType date;
	Struct Linknode *next;
*LiStack;

链栈所有操作都与链表相同这里就不一一罗列了，对链表不了解的可以先去看看数据结构之线性表。链栈与链表唯一一点不同的是栈的所有操作都只能在表头进行。

类似于入栈操作就是头插法，包括出栈之类的操作也只能在头部进行操作。

队列

队列的定义

队列(Queue） 只允许在表的一端进行插入，表的另一端进行删除操作的线性表，它的特性是先进先出(FIFO)

队列的基本操作

InitQueue(&Q)：初始化队列，构造一个空队列Q。
QueueEmpty(Q)：判队列空，若队列Q为空返回 true，否则返回false。
EnQueue(&Q, x)：入队，若队列Q未满，则将x加入使之成为新的队尾。
DeQueue(&Q, &x)：出队，若队列Q非空，则删除队头元素，并用x返回。
GetHead(Q, &x)：读队头元素，若队列Q非空则用x返回队头元素。
ClearQueue(&Q)：销毁队列，并释放队列Q占用的内存空间

队列根据存储结构也分为：顺序队列与链式队列。

顺序队列

所谓顺序队列就是采用顺序结构队列，它由一个数组和一个队头位置标记和一个队尾位置标记组成。

代码实现为：

# define MaxSize 50
typedef struct
	ElemType date[MaxSize];
	int front,rear;
 SqQueue;

front一般指向队头元素，rear一般指向队尾元素的下一位置。也可以front指向队头元素的前一位置，rear指向队尾元素。两种指向位置不同对应操作也不同，但是我们一般用前者，今天也是讲解前者。

我们插入元素时候是从队尾进入队列，从队头离开队列。

常用判断条件（传入队列为Q）

判断队空条件：Q.front==Q.rear
求队长：Q.rear-Q.front
判断队满条件：Q.rear==MaxSize

但是这里的判断队满条件是有问题的，试想如果队列都存满了即：Q.rear==MaxSize的时候队头出删除了一个元素，这时候队头指针会下移，并且空出来了一个队列位置，但是它依旧满足Q.rear==MaxSize判断队满的条件，这样就会出现假溢出问题了。

为了解决这个问题，我们请出今天队列的主角——循环队列，为什么说它是主角呢，因为我们用队列时候一般都用它！！

循环队列

首先要清楚循环队列只是逻辑上的循环，在内存上依然是顺序存储的，所以它仍然属于顺序队列。

那它是如何实现逻辑上的循环呢？

它把队列的尾部与首部在逻辑上连接起来了，即：当rear存储了最后一个元素位置的元素后直接跳到下标为0处。

如果队列没有移除元素，那么front就在下标为0处（即队头前无空数组），这时候rear与front就在同一个位置即：Q.front==Q.rear，此时队满。

如果队列移除了元素那么front就在下标不为0处（即队头前有空数组），这时还能向队列中加入元素，直至Q.front==Q.rear时，队列才满。

那它是怎么实现从最后位置到起始位置的呢？，，它依靠**取余%(MaxSize)**实现。

使用取余后，队列的front，rear，指针移动与求队列长度就都发生变化了，如下：

front指针移动：
Q.front = (Q.front + 1) % MaxSize
rear指针移动：
Q.rear = (Q.rear + 1) % MaxSize
队列长度：
(Q.rear + MaxSize - Q.front) % MaxSize

大家注意体会，可以自己画图试试指针的移动。

但是这时候问题又来了，如果你前面的都明白了，那你会发现现在判断队空与队满的条件一样了，都等于Q.front==Q.rear

很显然这样并不行，我们就得想办法改变其中之一的条件了，我们一般改变的是队满的判断条件，使得它们不一样。

方案一：

牺牲一个存储单元

就是最后一个存储单位不存放元素，这时候：

队空条件：Q.front==Q.rear
队满条件：Q.front==(Q.rear+1) %MaxSize

方案二：

增加一个变量代表元素的个数

就是在定义队列时候增加一个变量size来监控队列中存储元素的数量。这时候：

队空条件：Q.size== 0
队满条件：Q.size == MaxSize

还有其他的方案，大家主要还是根据场景变化来改变。

不过我们一般用的都是方案一，下面例子都是使用方案一实现的。

入队操作

bool EnQueue(SqQueue &Q,ElemType x)
	if(Q.front==(Q.rear+1)%MaxSize)
		return false;
	Q.date[Q.rear]=x;
	Q.rear = (Q.rear + 1) % MaxSize;
	return true;

出队操作

bool DeQueue(SqQueue &Q,ElemType &x)
	if(Q.rear == Q.front)
		return false;
	x=Q.date[Q.front];
	Q.front = (Q.front+1)%MaxSize;
	return true;

链式队列

链队就是采用链式存储的队列，它包括结点，一个头指针和一个尾指针。结点与链表定义的结点是相同的包括一个数据域和一个指针域。如下：

定义链队

typedef struct
	ElemType date;
	struct LinkNode *next;
LinkNode;

typedef struct
	LinkNode *front, *rear;
LinkQueue;

初始化链队

我们初始化的链表一般都是带头结点的链表，这样的好处我在线性表那节，已经说过了这里不做解释。

同时这里的链队也都是带头结点的

void InitQueue(LinkQueue &Q)
	Q.front = (LinkNode*)malloc(sizeof(LinkNode));
	Q,rear = Q.front;
	Q.front->next=NULL;

判断队空

bool isEmpty(LinkQueue Q)
	if(Q.front == Q.rear)
		return true;
	else
		return false;

入队操作

链队也是动态的所以不用怕队满，所以不需要判断队是否满了

void EnQueue(LinkQueue &Q,ElemType x)
	LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
	s->date=x;
	s->next=NULL;
	Q->rear->next=s;
	Q.rear=s;

出队操作

bool DeQueue(LinkQueue &Q,ElemType &x)
	if(Q.rear==Q.front)
		return false;
	LinkNode *p=Q.front->next;
	x=p->date;
	Q.front->next=p->next;
	if(Q.rear==p)
		Q.rear=Q.front;
	free(p);
	return true;

这里需要说明一下的就是这个if的判断语句是如果队列中只有一个元素在出队后，队中就没有元素了，此时应该Q.rear=Q.front

栈与队列的应用

在讲完栈与队列基础的东西之后我们就到有难度也是最实用的一个模块了，在讲应用之前先说一下它们各自的一些升华的知识。

栈与队列输入输出

在栈与队列中分别依次输入1，2，3，4它们的输出序列是什么呢？

在队列中输出序列必定是1，2，3，4因为它是先进先出嘛

但是栈中就不一定了。。

如果是连续的输入与输出，那么栈输出的必然是4，3，2，1这也没有什么可以争论的，但是如果输入输出是不连续的就一定是这个答案了

假设1先入栈，然后1立马就出栈了然后其他的数据也有变化，那么情况就很多很多了。

对1，2，3，4组合排列可得：

1234 1243 1324 1342 1423 1432
2134 2143 2314 2341 2413 2431
3124 3142 3214 3241 3412 3421
4123 4132 4213 4231 4312 4321

一共有24种，那么这24都可以作为栈的输出序列吗？

并不是，有些是不合法的。

譬如说4123

想要4先出栈，那么入栈顺序必定是1，2，3，4如果4先出栈，那么接下来肯定是3，2，1依次出栈了。

那么如果需要找到不合法的出栈序列这么多种我们要一个一个试吗？

不需要我们有一个准则，如果不符合这个准则那么就必然是不合法的出栈顺序

准则：出栈序列中每一个元素后面所有比它小的元素组成一个递减序列

有多少种出栈序列我们有一个公式可以算出来，如下：

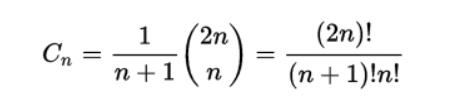
如果你想知道公式来由，你可以去出栈序列看看

双端队列

双端队列允许两端都可以进行入队以及出队操作的队列

之前我们学习的队列是容许在一端输入另一端输出，而双端队列是允许在两端都可以进行输入输出的，我愿称之为队列最强变异版。

其实在仔细一想你会发现这是两个栈拼接到一起了，只不过是屁股对着屁股而已

但是无论它怎么变化它总是先出的元素在前，后出的元素在序列后

还有两种是受限制的双端队列，一种是只允许一端输出，两端输入还有一种是只允许一段输入，两端输出。

双端队列可以实现栈输出序列不合法的序列，受限制的双端序列可以实现部分栈输出序列不合法的序列

这部分，没什么好说的，用的也不多大家知道了就好了。接下来我们说一下栈与队列的一些常用应用。

栈的应用

学习了栈你可能会觉得这东西没什么用，但是栈的用处十分庞大，我们经常会用它去解决各种问题，今天就来简单列举两个吧！

表达式求值

我们对于表达式有三种定义分别是：前缀表达式，中缀表达式，后缀表达式

所谓中缀表达式就是我们平时都在用的譬如：A+B

对于这个表达式把他转换为前缀表达式就是+AB，也就是运算符号放到前面

那么后缀表达式就是：AB+

我们在很多时候都会对三种表达式之间进行相互转换，我们可以手动进行转换，那么有没有办法我们通过程序编写出来呢？

当然可以，而且就用队列就可以，算法思想如下：

中缀表达式转换为后缀表达式算法思想

数字直接加入后缀表达式
运算符时：
a. 若为’(’ ，入栈；
b. 若为’)’，则依次把栈中的运算符加入后缀表达 式，直到出现’(’，并从栈中删除’(’；
c. 若为’+’，’-’，’*’，’/’，
· 栈空，入栈；
· 栈顶元素为’(’，入栈；
· 高于栈顶元素优先级，入栈；
· 否则，依次弹出栈顶运算符，直到一个优先级比 它低的运算符或’('为止；
d. 遍历完成，若栈非空依次弹出所有元素

同样我们也可以把后缀表达式转换为中缀表达式，如下：
算法思想：

顺序扫描后缀序列
· 若是数字压入栈中；
· 若是操作符，连续弹出栈中两个元素，按操作符计算并把结果压入栈中。
· 扫描完毕后栈顶为最后结果

你可以对一个式子进行，这个流程看能不能成功转换

括号匹配

大家都知道括号是成对存在的，那么怎么知道一堆括号序列中是否合法呢？
我们仍然使用队列算法，如下

算法思想：

1）初始一个空栈，顺序读入括号。
2）若是右括号，则与栈顶元素进行匹配
· 若匹配，则弹出栈顶元素并进行下一个元素
· 若不匹配，则该序列不合法
3）若是左括号，则压入栈中
4）若全部元素遍历完毕，栈中非空则序列不合法

递归

递归 ：若在一个函数、过程或数据结构的定义中又应用了它自身，则称它为递归定义的，简称递归

一个完整的递归由两部分构成：递归表达式和递归出口

最简单的递归莫过于斐波那契数了，看看它的结构：

int Fib(int n)
	if(n==0)
		return 0;
	else if(n==1)
		return 1;
	else 
		return Fib(n-1)+Fib(n-2);

这个里面递归表达式就是Fib(n-1)+Fib(n-2)，递归出口就是n等于1或者0时候

递归的精髓在于能否将原始问题转换为属性相同但规模较小的问题

那么递归哪里用到栈了呢？

· 在递归调用过程中，系统为每一层的返回点、局部变量、传入实参等开辟 了递归工作栈来进行数据存储，递归次数过多容易造成栈溢出

但是递归往往计算效率不高，就比如说这个斐波那契数吧，它在计算时有很多重复的数字依然在继续调用递归计算，比如Fib(2)它就得算好多次

递归对于栈运用还有：递归转换算法转换为非递归算法，往往需要借助栈来进行

因为这里主要是说栈的运用所以对递归就不深入解析，等后期会专门出一期递归算法的！

结语

栈与队列也是很简单的数据结构，相信大家只要用脑袋去思考，必然能够轻松的凯瑞它！

有问题欢迎指正！感谢~

坚持与努力，下一节是串，数组和广义表！

持续更新中…