数据结构从0到1第六篇:排序(下)
Posted 小唐学渣
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构从0到1第六篇:排序(下)相关的知识,希望对你有一定的参考价值。
文章目录
前言
本篇文章继续上一篇来探讨排序当中的冒泡排序,快排、归并排序和计数排序,关于上一篇的直接插入排序、希尔排序、选择排和堆排序我们就不探讨了。大家可以参考这篇文章:【数据结构从0到1】第五篇:排序(上)
一、常见排序算法的实现
1.1冒泡排序
首先我们用一张动图来展示冒泡排序:
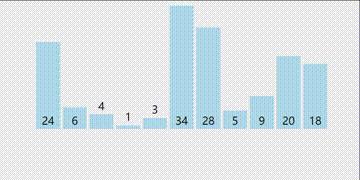
相信大家看完动图后都能够明白冒泡排序的原理了吧,其实就是前一个数和后一个数相比较,排升序的话,就把大的数往后面移,排降序就把小的数往后面移,那么我们就来实现一下:
首先我们先建立一个和上面相同的数组:
int a[] = 24, 6, 4, 1, 3, 34, 28, 5, 9, 20, 18 ;
第一步:单趟排序,将最大的数移到最后:
我们比较大小有两种方法:
第一种,下标从0开始和后面的数比较:

第二种:下标从1开始和前面的数比较:

我们就选择第二种方法比较

代码实现:
for (int i = 1; i < n - j; i++)
if (a[i - 1] > a[i])
Swap(&a[i - 1], &a[i]);
第二步:多趟排序,每次将最大的数都往后移,排成升序:

代码实现:
void BubbleSort(int* a, int n)
assert(a);
/*方法一:*/
/*控制多趟,排成有序*/
for (int j = 0; j < n; j++)
//方法二:
for (int i = 1; i < n - j; i++)
if (a[i - 1] > a[i])
Swap(&a[i - 1], &a[i]);
我们来通过打印数组来看一下排序是否成功:

此时我们发现没有错误。但是这样通过n - j 的方式控制单趟排序可能有些人认为有点麻烦,那么不妨来看另一种方法。此时我们我们可以同过一个end变量来控制边界:
时间复杂度 O(N^2)
void BubbleSort(int* a, int n)
assert(a);
// 方法二:
int end = n;
while (end)
for (int i = 1; i < end; i++)
// 控制单趟找出最大值
if (a[i - 1] > a[i])
Swap(&a[i - 1], &a[i]);
end--;
此时这样我们是不是更方便我们理解!!
那么我们来算一下冒泡排序的时间复杂度,(第一趟排序比较次数)+(第二趟排序比较次数)+…(最后一趟比较次数)= (n - 1)+ (n - 2)…+ 1,根据等差数列求和就是一个O(N^2)的时间复杂度了,当排的数据本身就是有序的时候,此时这个代码实现排序复杂度还是不变,那么我们可不可我一为优化一下这个代码呢?答案是可以的。
思路:如果第一趟排序我们发现是升序的话,我们就不进行后面的排序了,数组都有序了,我们就直接打印就是。首先定义以exchange变量,初始化为0
//定义exchange变量,用来检查这些数据是否有序
int exchange = 0;
for (int i = 1; i < end; i++)
if (a[i - 1] > a[i])
exchange = 1;
Swap(&a[i - 1], &a[i]);
然后根据exchange是否被改变判断数组是否是升序:
//假如本身就是有序的话,上面排序的时间复杂度还是O(N^2)
//我们现在优化一下数组本身就是有序或则数组接近有序的的情况。
void BubbleSort(int* a, int n)
assert(a);
int end = n;
//控制多趟排序
while (end)
//定义exchange变量,用来检查这些数据是否有序
int exchange = 0;
for (int i = 1; i < end; i++)
if (a[i - 1] > a[i])
exchange = 1;
Swap(&a[i - 1], &a[i]);
//单趟排序完成后,判断整个数组是否有序
if (exchange == 0)
break;
end--;
这样我们再来算一下时间复杂度,当是乱序的情况下很显然时间复杂度是O(N^2),但是当是有序的情况下时间复杂度就是O(N)了,我们也就达到了优化的目的。
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
此时我们来横线对比一下直接插入排序、直接选择排序和冒泡排序,最差的排序肯定大家都能想到,肯定是直接选择排序,因为不管是有序还是无序,时间复杂度都是O(N^2),但是直接插入排序和冒泡排序在有序的情况下时间复杂度是O(N),那么我们现在要在它们两个当中选出一个最好的,那么我们选哪个呢?
相信大家很难判断出来,那么我们来举个例子吧,假设现在有一个数组
int a[] = 1, 2, 3, 5, 4 ;
我们用直接插入排序算比较次数就是:5次,2和1比较一次,3和2比较…,最后4和5比较一次4和3比较一次。
我们用冒泡排序来算比较次数 4 + 3次就是7次。相信大家都能算出来。
我们将数据放大为n,最后两个无序,前面的都有序,直接插入排序的比较次数就是n次,而冒泡排序的比较次数就是(n-1)+(n-2)次。那么我们看到是不是直接插入排序相比较于冒泡来讲是会更优一点的。冒泡的实现相对比较简单,我们接下来的快排可能相对比较难。
1.2 快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:.任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
这个是什么意思呢?我们用动图演示:
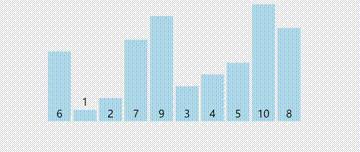
哎,这是怎么变换的呢?我们一步一步来看。
首先我们还是先建一个和上面动图相同的数组
int a[] = 6, 1, 2, 7, 9, 3, 4, 5, 10, 8 ;
快排的单趟排序就是选出一个数作为key值,然后再遍历数组将小于key值的数放在前面大于key值的数放在后面,然后我们来进行单趟排序,单趟排序有三种方法,我们先将最初始的方法。
1.2.1递归版本
1.2.1.1hoare版本
假设我们现在最左边的数作为key值,如图:

第一步:右边先走,去找比key小的数,找到就停下:

第二步:左边再走,去找比key大的数,找到就停下:
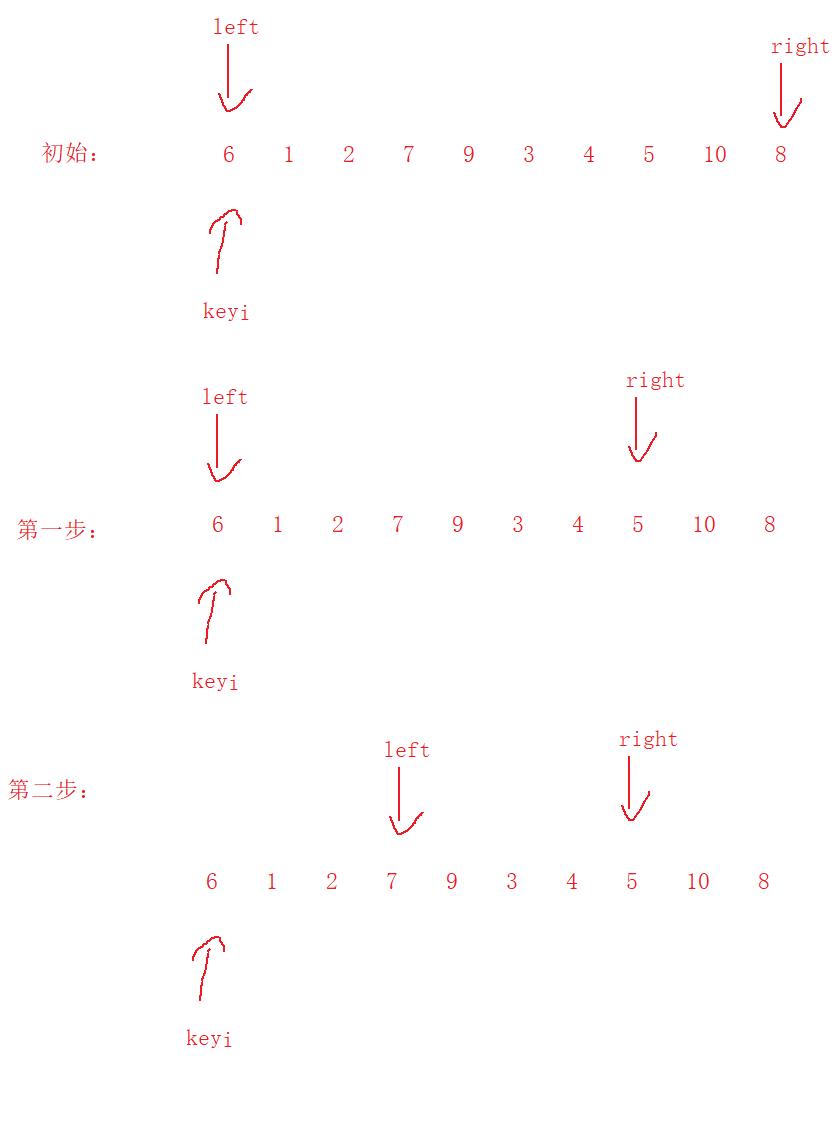
第三步:交换这两个数:
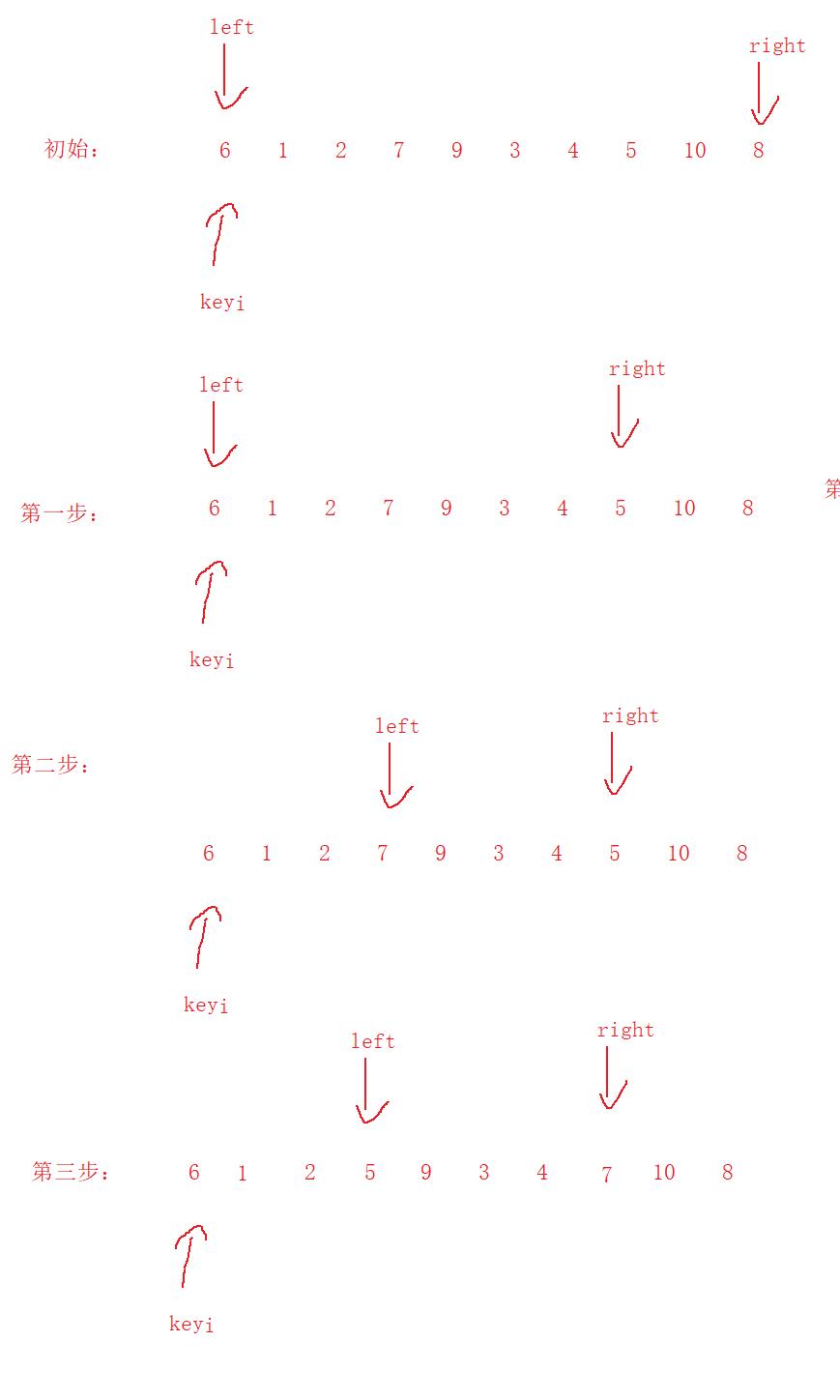
第四步:重复上面操作,直到left大于等于right停下。
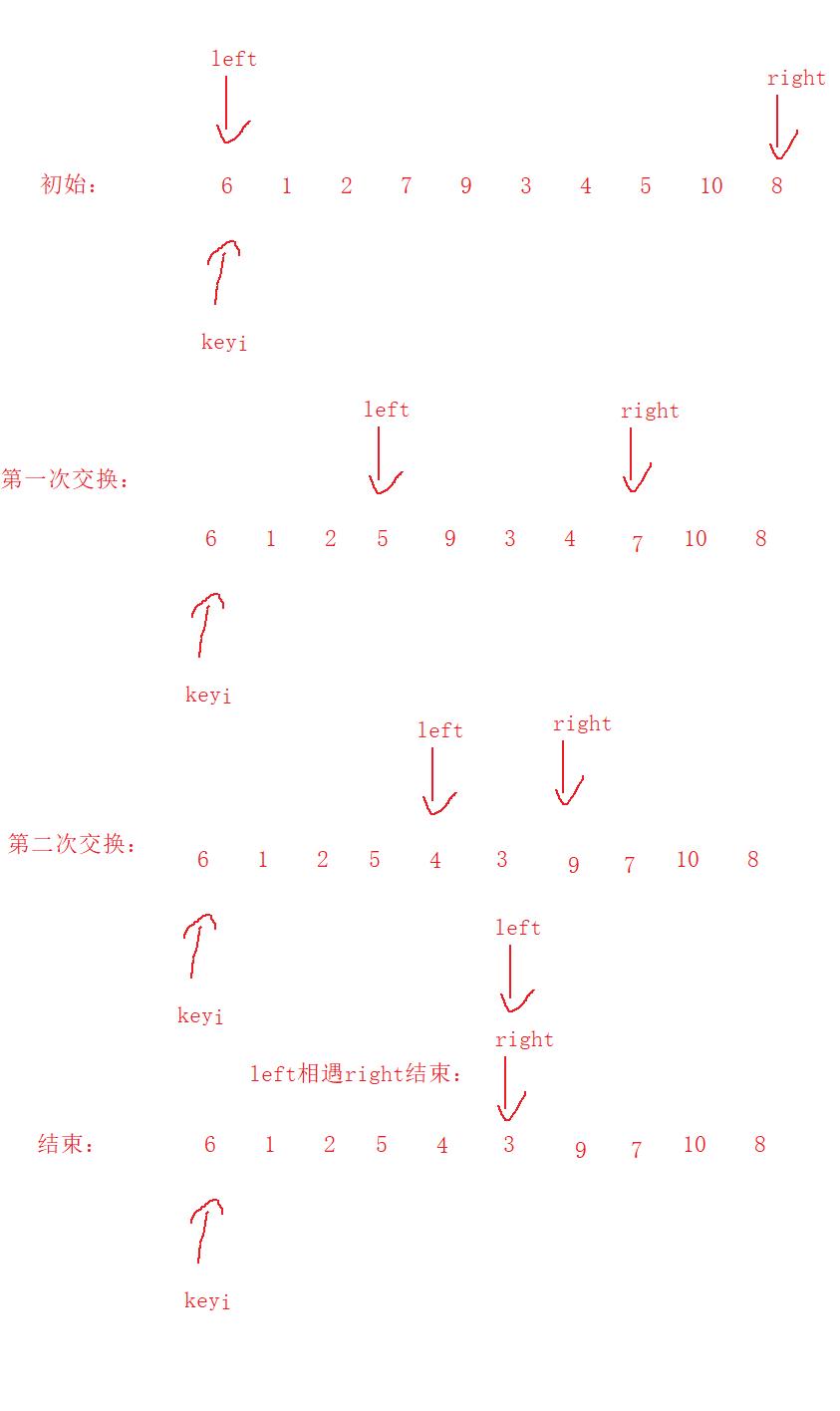
第五步:交换key的值和 left的值或者key的值和right值
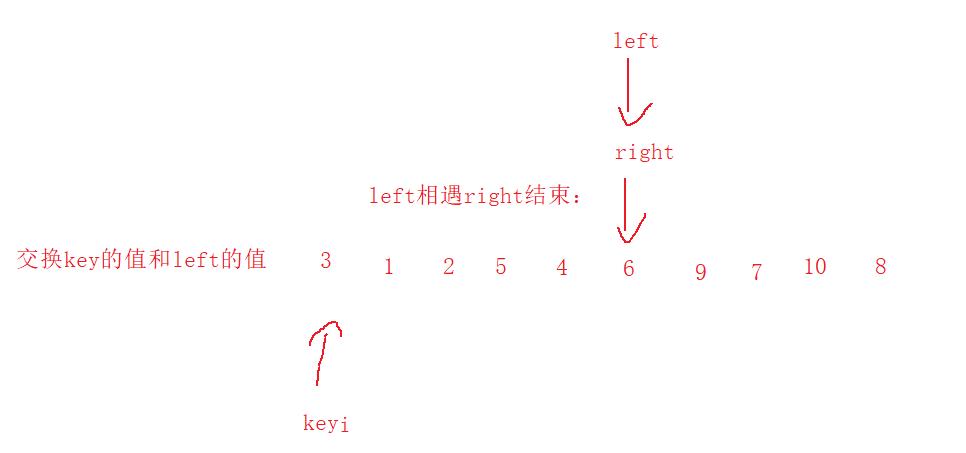
代码实现:
//1. hoare版本
int Partion1(int* a, int left, int right)
assert(a);
int keyi = left;
while (left < right)
//右边找小
while (a[right] >= a[keyi])
right--;
//左边找大
while (a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
//最后交换keyi位置的值和相遇位置的值。
Swap(&a[keyi], &a[left]);
return left;
同理:上面的单趟排选最右边的数作为key也是一样的,那么大家可能会有这样一个疑问?我们为什么选最左边作为key的时候,先走的右边,而中间相遇的值为什么又比key小呢?这其实是一个问题,我们先画图分析。
假设我们现在左边作为key,而左边先走:

此时我们就发现9被交换到前面去了,所以在最左边作key的时候,我们就要先走right,因为不管是当数组在交换n次之后,最后一次先走的还是right,如果找到小了,就停下,等left和它相遇,此时交换就是比key小,而如果right没有找到,最后也要和left相遇,此时相遇left指向的还是比key小的数。
我们在看单趟排序的代码大家可能很快就发现了错误,因为可能left和right不会相遇
比如说数组元素是一样的时候或则数组是升序的时候:
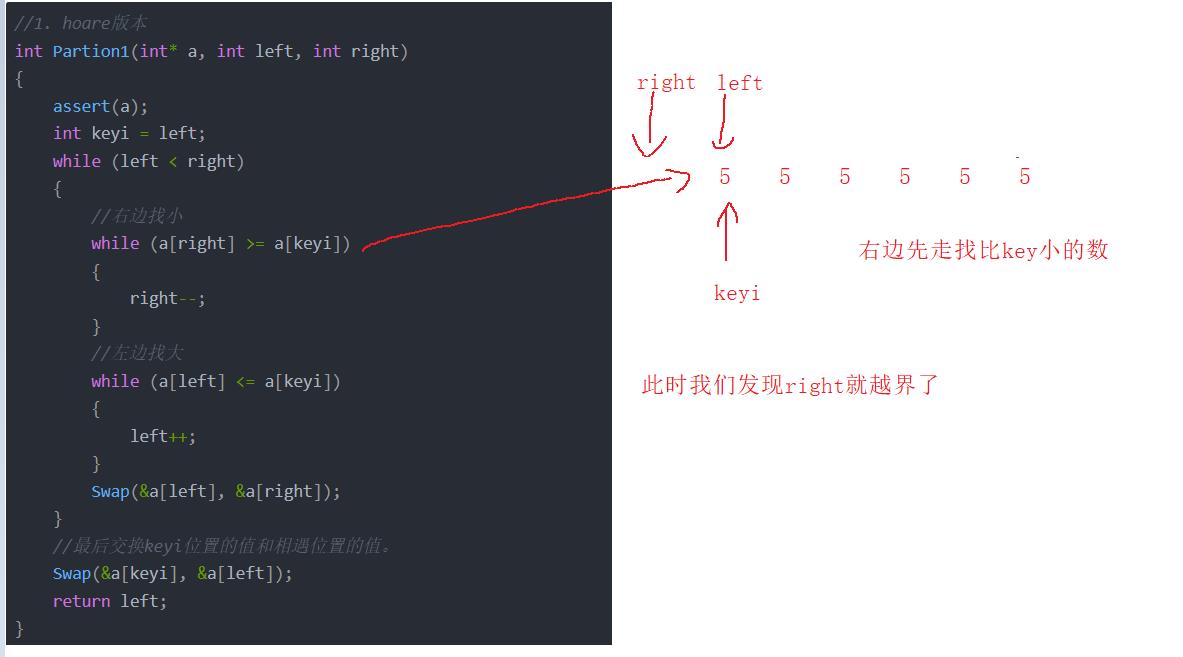
那么我们在上面修改一下代码:
//1. hoare版本
int Partion1(int* a, int left, int right)
assert(a);
int keyi = left;
while (left < right)
//右边找小
while (left < right && a[right] >= a[keyi])
right--;
//左边找大
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
//最后交换keyi位置的值和相遇位置的值。
Swap(&a[keyi], &a[left]);
return left;
此时我们单趟排序就完成了,此时相遇点左边的值都比key小,而右边的值都比key大。我们就做到将一个数排成有序了。但是我们要排的是多个数,此时我们是不是可以又去递归它的左区间和它的右区间,将每个区间的值都排好,那么我们整个数组是不是也就排好了。这就跟二叉树的遍历差不多,我们先打印,再递归左子树和右子树。
我们画图演示:
代码实现:
int Partion1(int* a, int left, int right)
assert(a);
int keyi = left;
while (left < right)
//右边找小
while (left < right && a[right] >= a[keyi])
right--;
//左边找大
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
//最后交换keyi位置的值和相遇位置的值。
Swap(&a[keyi], &a[left]);
return left;
//时间复杂度:O(N*logN)
void QuickSort(int* a, int left, int right)
assert(a);
if (left >= right)
return;
int keyi = Partion1(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
我们先来测试一下代码是否能排成升序:
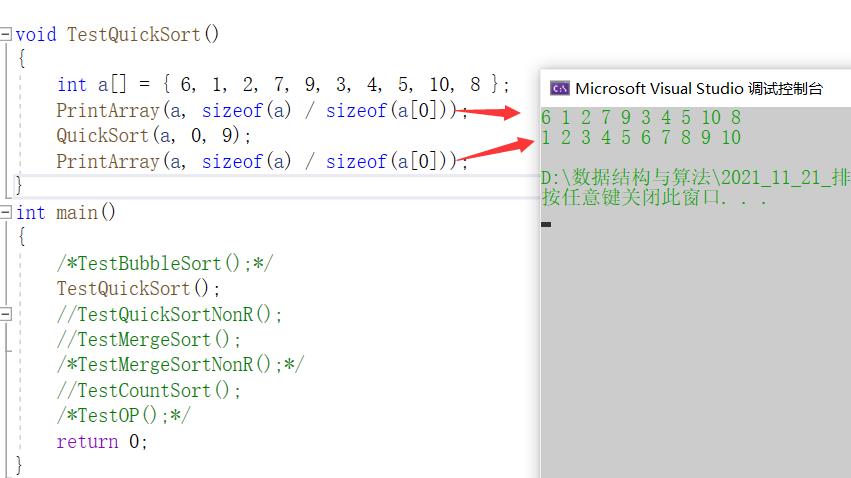
接下来为了更好理解我们就来画递归展开图:

相信大家大概又有了更深的印象了吧!那么我们来测试1000000个数来看一下:
void TestOP()
srand(time(0));
const int N = 1000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2= (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
/*int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();*/
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
/*int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();*/
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
/*int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();*/
//printf("InsertSort:%d\\n", end1 - begin1);
printf("ShellSort:%d\\n", end2 - begin2);
//printf("SelectSort:%d\\n", end3 - begin3);
printf("HeapSort:%d\\n", end4 - begin4);
printf("QuickSort:%d\\n", end5 - begin5);
/*printf("MergeSort:%d\\n", end6 - begin6);*/
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
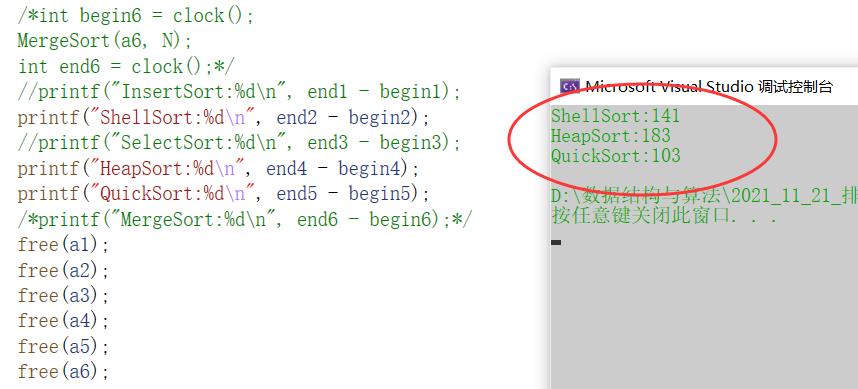
此时我们看到基本上希尔排序、堆排序和快排都差不多的。因为时间复杂度大概都是O(NlogN)
那么快排就完了吗?就这么简单?快排有什么缺陷没有?那可肯定是有的:我们刚刚排的数组,每次选可key的时候,都基本上是选的中位数,所以时间复杂度就是O(NlogN),那么我们此时选key不是选的中位数,那么排序的时间复杂度就会变成O(N^2)了。
怎么证明呢?
我们分析选key每次都选的是中位数或则接近于中位数:
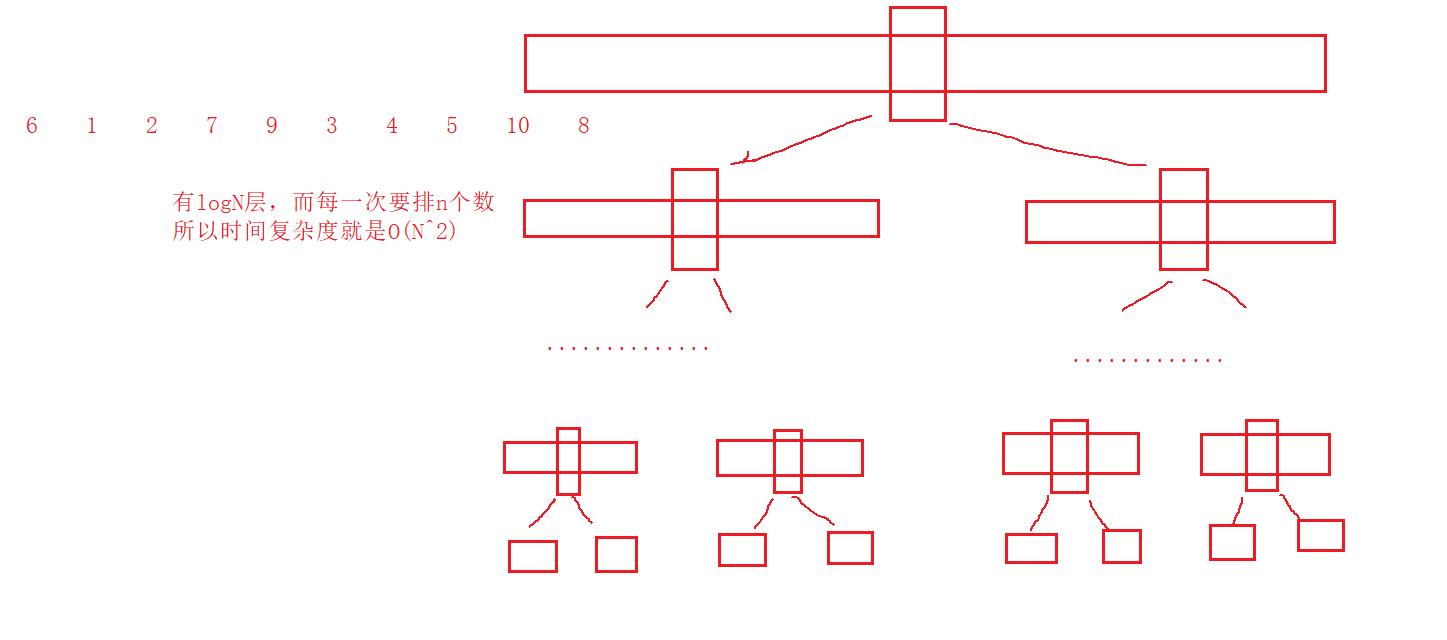
如果此时我们的数组是有序的:
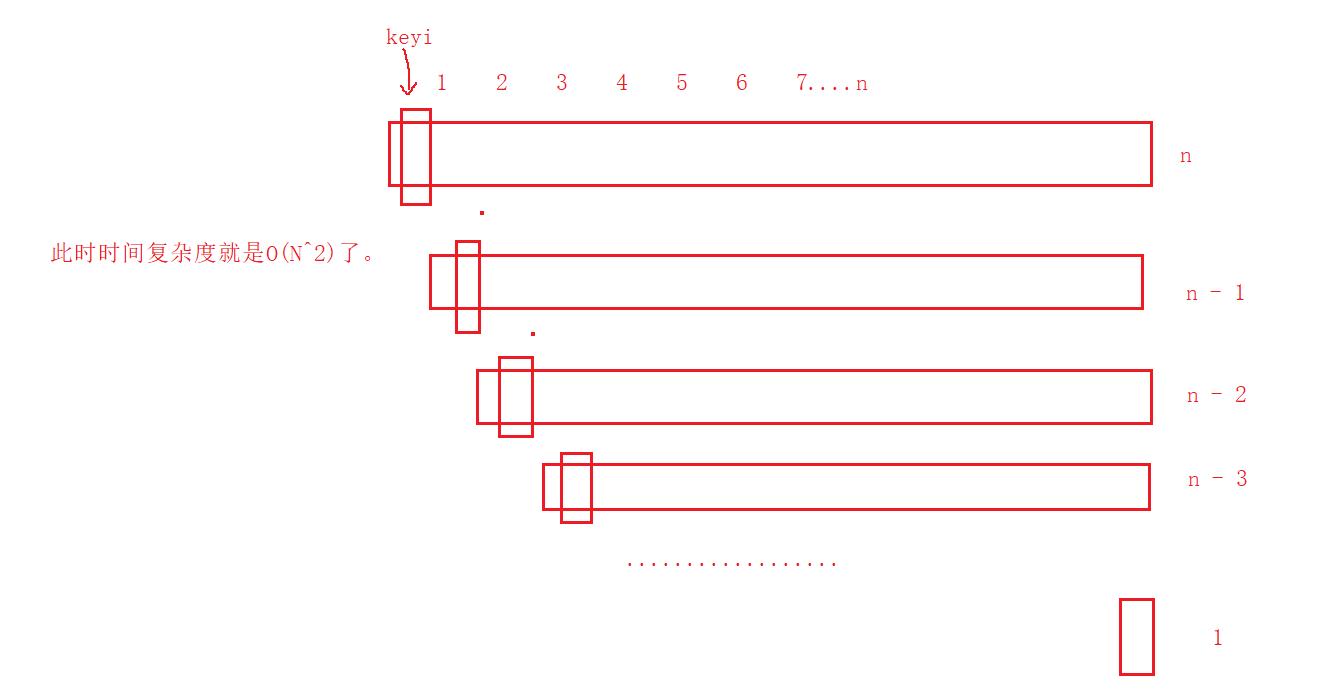
不光是时间复杂度变了,我们递归调用还肯能要栈溢出。我们可以测试一下
void TestOP()
srand(time(0));
const int N = 1000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2= (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
/*int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();*/
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
/*int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();*/
int begin4 = clock();
HeapSort(a2, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a2, 0, N - 1);
int end5 = clock();
/*int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();*/
//printf("InsertSort:%d\\n", end1 - begin1);
printf("ShellSort:%d\\n", end2
