分数的全面解析式与在C语言中应用分数计算

Posted 2021-12-19 17岁boy想当攻城狮

分数的概念

分数就是将一个整体拆分成多少份，并选其中的几份，也就是将1拆分。

比如一个大蛋糕，我们看成一个整体“1”，并拆分成5份，就是将一整块蛋糕拆分成5小块，然后取其中的“3”分，写成分数就是：

分数起源于古埃及，最初古埃及数学家发明一种公式，用来计算分东西的一些计算场景，就如开始说的分蛋糕，就是将1平均分成若干份，然后在选其中的几份，在不能拆分整数的情况下用一种新的公式来表示整数分成。

分子

写在分数线上面的数

分母

写在分数线下面的数

整数与分数之间的转换

如有“1000”个冰激凌，我们把它看作一个整体“1”，然后平均分成8份，选其中的4份用来分。

那么数学表达就是：

首先要知道分母表示了平均分成了几份，那么我们通过分母转整数就知道8份里平均每份有多少个，那么我们只需要拿“1000/8”，整数除以分母就得出了平均分的数：

“1000/8=125”

因为分母是分了多少份，那么具体是分谁的？肯定是分冰激凌数量的，所以拿数量除于多少份就可以得到平均分了几份

然后我们在取分子，分子的意思是取其中的多少份，分子是4，所以就是取其中的4份。

刚刚进行了计算，分母平均每份是125个，有8份，然后分子的意思是取其中的4份，我们拿“125*4”就可以了

“125*4=500”

也就是说实际上分了500个

那么接下来我们用C语言写一个函数，用于完成上面的计算。

#include <stdio.h>

int ScoreCalculation(int Integer/*整数*/,int Denominator/*分母*/,int Molecule/*分子*/)
    
    //首先第一步先取出平均分的数
    int TempNumber = (Integer / Denominator);
    //然后第二步用表示分了多少份的分子乘上平均分的数就可以了
    return (Molecule * TempNumber);


int main()

    printk("Scor:%d\\n",ScoreCalculation(10000,8,4));
    return 0;

非常简单

分数比大小

在分数比大小时，大家要记住比的是什么，分数比的是平均分下来数的总大小

比如刚刚说的1000分成：分8份，每份分125个，记住这125就是平均分的数的大小，而4是取其中的多少份，那么取其中的4份就代表平均分下来数的总大小是：“4*125=500”，这里500就是我们要比的数。

当遇到一些有整数的分数我们可以将它转化为整数然后比较，用刚刚的思路。

但是通常数学题里不会给出整数，但是我们通过分数的定律就知道，分母越小，平均分的数肯定就越大，分子也更小的情况下就代表这个分的数的总大小就非常大。

如

试试看，转化成C语言代码，用最基础的方式，将分数转化为整数的方式比大小：

#include <stdio.h>

//如果A大于B返回True，否则返回False
bool SpecificSize(int Integer,int A_Denominator,int A_Numerator,
                  int B_Denominator,int B_Numerator)
        
        //先将分数A转化为整数
        int Temp_A = (Integer / A_Denominator);
        //取出分数A分成的总数量
        int Temp_A_Number = (Temp_A * A_Numerator);
        
        //B也一样
        int Temp_B = (Integer / B_Denominator);
        int Temp_B_Number = (Temp_B * B_Numerator);

        //然后直接比大小
        return (Temp_A_Number > Temp_B_Number ? true : false);

通过定律，有三个可以不需要计算的数学公式：

1.分子相等时，分母越小，这个分数就越大

因为我们把分数拆开来看其实就是一个整数，比如整数是1000，分成和

那么我们可以按照刚刚的思路，把它们转化为整数：

=500

=800

那么比较起来是不是就一目了然了？800肯定比500大。

那么有这个方法我们就可以改进第一个代码

#include <stdio.h>

//如果A大于B返回True，否则返回False
bool SpecificSize(int Integer,int A_Denominator,int A_Numerator,
                  int B_Denominator,int B_Numerator)
        
        //判断第一个情况分子是否相同
        if(A_Numerator == B_Numerator)
                
                //直接判断分母
                return (A_Denominator < B_Denominator) ? true : false;
        
    
        //先将分数A转化为整数
        int Temp_A = (Integer / A_Denominator);
        //取出分数A分成的总数量
        int Temp_A_Number = (Temp_A * A_Numerator);
        
        //B也一样
        int Temp_B = (Integer / B_Denominator);
        int Temp_B_Number = (Temp_B * B_Numerator);

        //然后直接比大小
        return (Temp_A_Number > Temp_B_Number ? true : false);

2.分母相等时，分子越大，这个分数就越大

这个我想只要大家理解了第一个说的，这个就非常简单，因为分母相等的情况下意味着平均分的数就一样了，那么只需要知道分的多的那一方就是最大的。

就如1000分成与

很明显第一个是：500

第二个是：875

因为第一个平均分了8份每份分了125个，然后取其中4份可用就是4*125=500，所以实际分了500个

第二个就是取了7份就是：“7*125=875”

所以谁大一目了然

那么依然可以修改上面的代码

#include <stdio.h>

//如果A大于B返回True，否则返回False
bool SpecificSize(int Integer,int A_Denominator,int A_Numerator,
                  int B_Denominator,int B_Numerator)
        
        //判断第一个情况分子是否相同
        if(A_Numerator == B_Numerator)
                
                //直接判断分母
                return (A_Denominator < B_Denominator) ? true : false;
        
        
        //判断第二个情况，分母是否相同
        if(A_Denominator == B_Denominator)

                //直接判断分子
                return (A_Numerator > B_Numerator) ? true : false;
        

        //先将分数A转化为整数
        int Temp_A = (Integer / A_Denominator);
        //取出分数A分成的总数量
        int Temp_A_Number = (Temp_A * A_Numerator);
        
        //B也一样
        int Temp_B = (Integer / B_Denominator);
        int Temp_B_Number = (Temp_B * B_Numerator);

        //然后直接比大小
        return (Temp_A_Number > Temp_B_Number ? true : false);

3.分母分子都不同，先通分在比大小

通分

通分就是将分母转化为相同数

首先说一下通分的过程：

1.先分别列出两个分母的约数（也叫因数）

2.将分母乘上另外一个分母的最小公约数

比如与比较大小，首先我们将两个分数的分母取出来

7 与 5

然后用断除法取到两个数之间约数

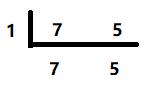
经过除法，7与5只能被1整除，所以它们的共同约数只有“1”

然后我们要取出最小公倍数，就是约数乘上“质因数”：1*7*5=35

然后将分母转化为最小公倍数，7转化为公约数就是乘上5，5转化为最小公倍数就是乘上7

你会发现一个现象，就是分母转化为最小公倍数时就是乘上另外一个分母经过短除法分解后的质数：

7*5=35

5*7=35

然后为了保证分数大小不变，分母变了分子也要做相应的变化，分母乘上了5与7，那么分子之间也做同样的操作

 9*5=45

3*7=21

经过上面的转化，就变成了：

=

=

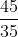
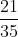
这是最基础的分解法求最小公倍数，原理就是将两个数进行整除，一直除到两个数不能再被整除为止，也就是双方的商最后都为质因数。

然后将除后的约数进行相乘在乘上双方的质因数就得到两个分母的最小公倍数，这是一个得到最小公倍数的计算公式。

这里来说一下为什么要使用最小公倍数来作为两个异分母的共同分母，原因在于公倍数是可以被异分母整除的，同时你可以不使用最小公倍数，使用其它公倍数结果也是一样的，使用最小公倍数只是最简化数字，不然数字会非常大，但结果是一样的。

然后在此时就非常好比大小了，可以用最开始的公式，分母相同分子越大这个数就越大。

所以是>

试试看，将上面的计算步骤转化为C语言代码

#include <stdio.h>

//如果A大于B返回True，否则返回False
bool SpecificSize(int A_Denominator,int A_Numerator,
                  int B_Denominator,int B_Numerator)
        
        //先求出两个分母之间的公约数
        int Temp[1024] = 0;
        int Index = 0;
        //因为公约数是能被两数整除的，随便选一个分母数，然后递减就可以了
        int A_Prime = 0;    //A与B的质数
        int B_Prime = 0;
        for(int i = A_Denominator;i>=1;--i)
            
                if((A_Denominator % i != 0) && (B_Denominator % i != 0))

                    Temp[Index++] = i;
                    A_Prime = (A_Denominator / i);
                    B_Prime = (B_Denominator / i);

                
                
        
        
        //在求出最大公倍数
        //就是公约数乘上质数
        int Temp_Number = Temp[0];
        for(int i = 1;i<Index;++i)

            Temp_Number *= Temp[i];
        
        //乘上质数
        Temp_Number = Temp_Number * A_Prime * B_Prime;
        //这里有两种写法将分母转化为最小公倍数
        //1. 分母乘于另外一个分母的质数
        //2. 分母直接替换成已经计算出的最小公倍数
        //分母
        A_Denominator = A_Denominator * B_Prime;
        B_Denominator = B_Denominator * A_Prime;
        //分子
        A_Numerator   = A_Numerator * B_Prime;
        B_Numerator   = B_Numerator * A_Prime;
        
        //最终用分子做比较
        if(A_Numerator > B_Numerator)

            return true;
        else
                
            return false;
        

其实在C语言里有更方便的写法，但是为了突出与数学上的解题过程，所以是一步一步写的。

分数的加减乘除

分数加减法：同分母分数相加减，分母不变，分子相加减；异分母分数相加，先通分再计算，结果能约分要约分。

有这个原理，我们写一个代码来实现分数的加法：

#include <stdio.h>

void Add(int A_Denominator,int A_Molecule,int B_Denominator,int B_Molecule)


        //首先看看分母是否相同
        if(A_Denominator == B_Denominator)

            //分母相同，计算分子，然后直接输出结果
            A_Molecule = A_Molecule + B_Molecule;
            printf("Denominator:%d,Molecule:%d\\n",A_Denominator,A_Molecule);
            return;
            
        
        //不相同的情况下我们需要通分
        int Temp = 1;
        int A;    //这两个数用于计算最后的质因数
        int B;
        //下面这段代码实现了分解公式
        for(int i = 0;i<A_Denominator;++i)
            
            if(A_Denominator%i==0 && B_Denominator%i==0)

                Temp = Temp * i;
                A = A_Denominator / i;
                B = B_Denominator / i;
            

        
        //得到最小公倍数
        Temp = Temp * A_Denominator * B_Denominator;
        //为了保持数的正确性分子也要进行计算
        //分子需要乘上分母的约数
        A_Molecule = A_Molecule * (A_Denominator / Temp);
        B_Molecule = B_Molecule * (B_Denominator / Temp);
          
        //相加
        A_Molecule = A_Molecule + B_Molecule;
        printf("Denominator:%d,Molecule:%d\\n",Temp,A_Molecule);
        return;
        

减法也是如此，只需要修改一下上面的代码将加符号改成减符号就可以了。

乘法就更简单了：分数相乘，用分子乘积做分子，分母乘积做分母；分数乘整数，分子和整数乘积做分子。

#include <stdio.h>

void multiplication(int A_Denominator,int A_Molecule,int B_Denominator,int B_Molecule)

        printf("Denominator:%d,Molecule:%d\\n",A_Denominator * B_Denominator ,A_Molecule * B_Molecule);
        return;
        

分数除法：分数相除，等于乘以该分数的倒数，结果化简。

倒数就是相反数，这里需要注意将哪个数变成倒数，变成倒数的是除数，被除数不变，然后在按照乘法来计算就可以了。

如：进行倒数后变成：然后在按照乘法方式进行乘法计算：

#include <stdio.h>

void division(int A_Denominator,int A_Molecule,int B_Denominator,int B_Molecule)

        printf("Denominator:%d,Molecule:%d\\n",A_Denominator * B_Molecule,A_Molecule * B_Denominator);
        return;
        

代码非常简单就是将除数倒过来了。

上面的计算结果都没有进行约分，那么接下来讲一下约分：

约分就是将分母与分子同时除于公约数，然后分数不变

写一个代码来进行约分

#include <stdio.h>

void About_Points(int A_Denominator,int A_Molecule)

        //短除法求个最大公约数
        int Temp;
        for(int i = A_Denominator;i<=0;--i)

                if(A_Denominator%%i==0 && A_Molecule%%i==0)
                    
                    Temp = i;
                    printf("%d,%d",A_Denominator / Temp,B_Denominator / Temp);
                
        
        
        return;
        

你可以不使用最大公约数，任何一个公约数仍然可以。

上面我只是有方便的方法找到最大公约数，如果你有方法可以快速找到任何一个公约数仍然是可行的，数学不是死的。