《LeetCode零基础指南》(第三讲) 循环
Posted 英雄哪里出来
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《LeetCode零基础指南》(第三讲) 循环相关的知识，希望对你有一定的参考价值。
文章目录
零、了解网站
1、输入输出
对于算法而言，就是给定一些输入，得到一些输出，在一般的在线评测系统中，我们需要自己手写输入输出函数（例如 C语言中的scanf和printf），而在 LeetCode 这个平台，只需要实现它提供的函数即可。函数的传入参数就代表了的算法的输入，而函数的返回值则代表了的算法的输出。
2、刷题步骤
找到一道题，以 两整数之和 为例，如何把这道题通过呢？如下图所示：
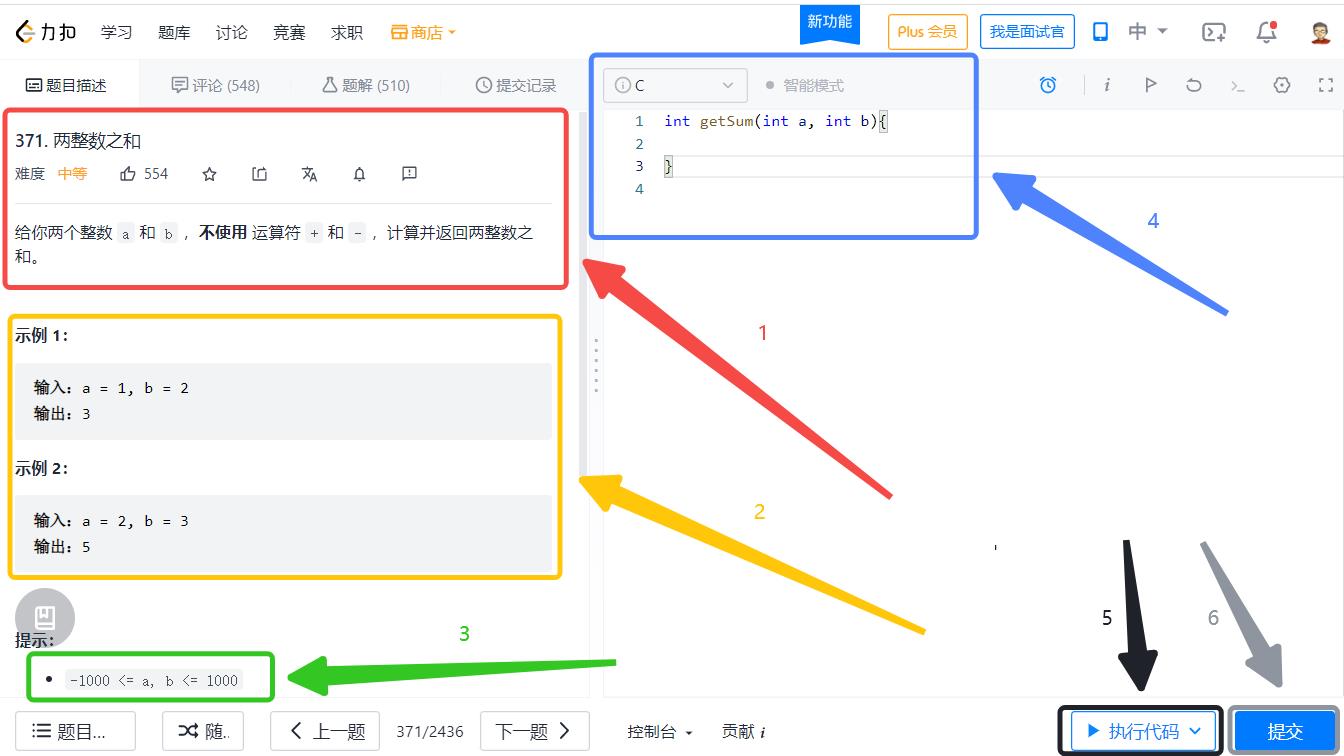
第 1 步：阅读题目；
第 2 步：参考示例；
第 3 步：思考数据范围；
第 4 步：根据题意，实现函数的功能；
第 5 步：本地数据测试；
第 6 步：提交；
3、尝试编码
这个题目比较简单，就是求两个数的和，我们可以在编码区域尝试敲下这么一段代码。
int getSum(int a, int b) // (1)
return a + b; // (2)
-
(
1
)
(1)
(1) 这里
int是C/C++中的一种类型，代表整数，即 Integer，传入参数是两个整数； - ( 2 ) (2) (2) 题目要求返回两个整数的和，我们用加法运算符实现两个整数的加法；
4、调试提交
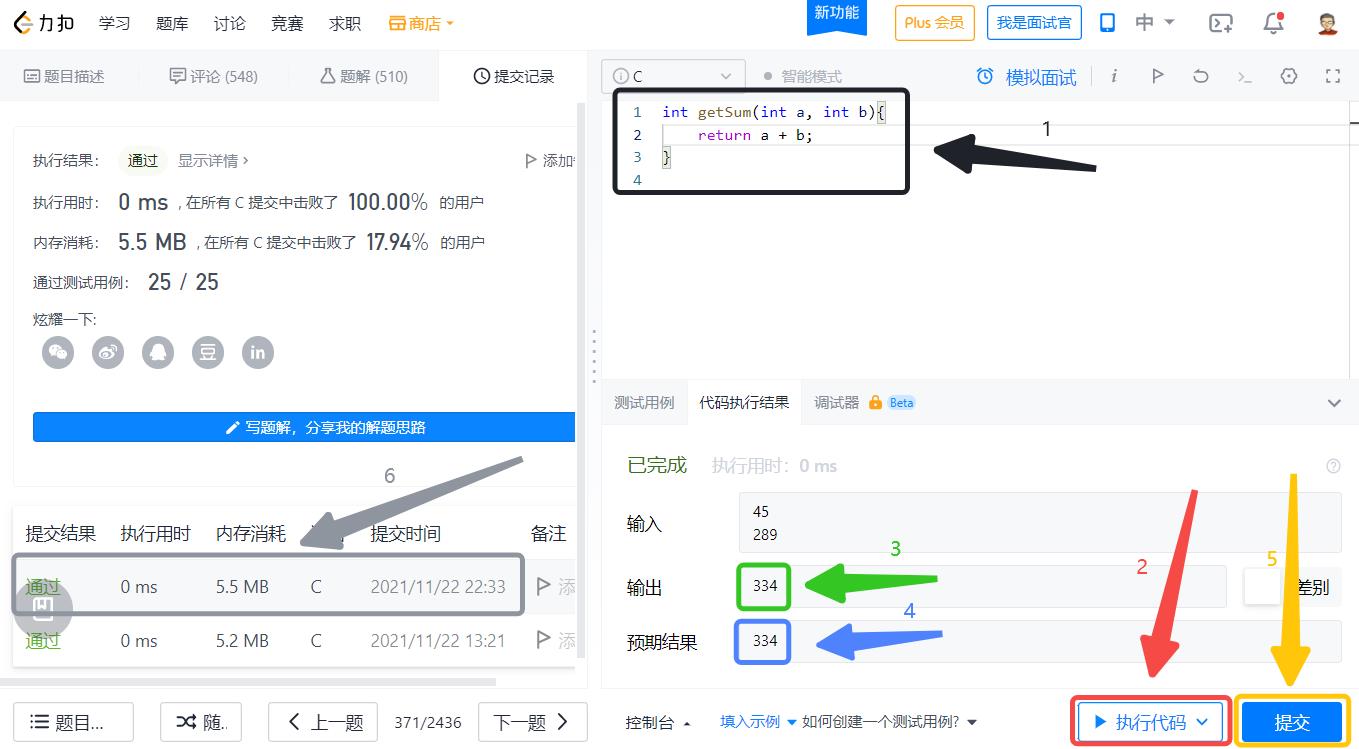
第 1 步：实现加法，将值返回；
第 2 步：执行代码，进行测试数据的调试；
第 3 步：代码的实际输出；
第 4 步：期望的输出，如果两者符合，则代表这一组数据通过（但是不代表所有数据都能通过哦）；
第 5 步：尝试提交代码；
第 6 步：提交通过，撒花 🌻🌼🌺🌷🥀；
这样，我们就大致知道了一个刷题的步骤了。上一章我们了解了函数，并且，实际编码的过程只有一行代码。这次我们来学习一下 循环。
一、概念定义
对于循环来说，C/C++ 语言中总共有两种结构，while 和 for，但是对于刷题来说，其实两者没有本质区别，所以这里我只介绍相对较为简单的 for 语句。
1、语法规则
for 语句的一般形式为：
for(循环初始化表达式; 循环条件表达式; 循环执行表达式)
循环体
它的运行过程为：
1）首先，执行 循环初始化表达式；
2）然后，执行 循环条件表达式，如果它的值为真，则执行循环体，否则结束循环；
3）接着，执行完循环体后再执行 循环执行表达式；
4）重复执行步骤 2）和 3），直到 循环条件表达式 的值为假，则结束循环。
上面的步骤中，2）和 3）是一次循环，会重复执行，for 语句的主要作用就是不断执行步骤 2）和 3）。执行过程如下图所示：
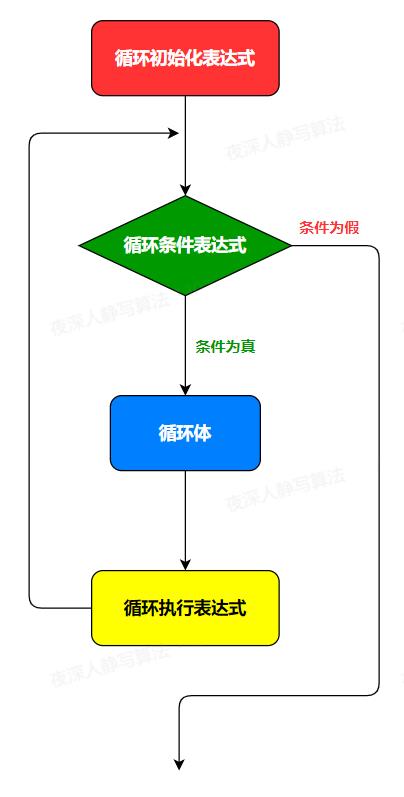
细心的读者可能会发现，循环体 和 循环执行表达式 其实是可以合并的，是的，的确是这样。在下面的例子中我会讲到。
2、简单应用
接下来，我们就来实现一个最简单的循环语句，求 1 + 2 + 3 + . . . + n 1 + 2 + 3 + ... + n 1+2+3+...+n 的值。
int sumNums(int n) // (1)
int i; // (2)
int sum = 0; // (3)
for(i = 1; i <= n; ++i) // (4)
sum += i; // (5)
return sum; // (6)
- ( 1 ) (1) (1) 这是一个函数，传参是 n n n，返回值为 1 + 2 + 3 + . . . + n 1 + 2 + 3 + ... + n 1+2+3+...+n 的值；
- ( 2 ) (2) (2) i i i 作为一个循环变量；
- ( 3 ) (3) (3) 初始化求和的值 s s s 为 0；
-
(
4
)
(4)
(4) for 语句三部分：循环初始化表达式：
i = 1；循环条件表达式：i <= n；循环执行表达式：++i； -
(
5
)
(5)
(5) 循环体：
sum += i;，表示将 1、2、3、4、… 累加到sum上； -
(
6
)
(6)
(6) 返回求和
sum的值；
以上这段代码，实现了一个数学上的 等差数列 求和。也可以用公式来表示，如下： s u m = ( 1 + n ) n 2 sum = \\frac (1 + n)n 2 sum=2(1+n)n而利用 for 循环，让我们抛开了数学思维，用程序的角度来实现数学问题。
注意，for 循环中的那个表达式都可以省略，但它们之间的 分号 必须保留。
3、初始化表达式
1）初始化表达式外置
我们可以把 初始化表达式 提到 for 循环外面，如下：
int i = 1; // (2)
int sum = 0; // (3)
for(; i <= n; ++i) // (4)
sum += i; // (5)
其中注释中的编号对应上文代码中的编号。
2）初始化表达式内置
我们也可以把需要的初始化信息，都在 初始化表达式 内进行赋值，并且用逗号进行分隔，如下：
int i, sum;
for(i = 1, sum = 0; i <= n; ++i) // (4)
sum += i; // (5)
具体选择哪种方式，是 代码规范 的问题，不在本文进行讨论，都是可以的。
4、条件表达式
如果省略 条件表达式，那就代表这个循环是一个 死循环，如下：
int i; // (2)
int sum = 0; // (3)
for(i = 1;; ++i) // (4)
sum += i; // (5)
这段代码表示这个循环没有 结束条件，那自然就不会结束了，编码过程中应该尽量避免（当然，某些情况下还是需要的，例如游戏开发中的主循环），或者，函数内部有能够跳出函数的方法，比如 break 关键字。
5、执行表达式
执行表达式 的作用是 让循环条件 逐渐 不成立，从而跳出循环。
当然，它也是可以省略的，因为 循环体 本身也是一个 语句块，也可以达到类似功能，如下代码所示：
int i, sum = 0; // (2)
for(i = 1; i <= n;) // (3)
sum += i; // (4)
++i;
这段代码同样达到了求和的功能，因为 执行表达式 被放入了 循环体，这也正是上文所说的 循环体 和 循环执行表达式 合并的问题。
二、题目分析
1、2 的 幂
实现一个函数
isPowerOfTwo，判断一个 32位整型 n n n 是否是 2 的幂。
bool isPowerOfTwo(int n)
int i;
unsigned int k = 1; // (1)
if(n <= 0)
return false; // (2)
if(n == 1)
return true; // (3)
for(i = 1; i <= 31; ++i)
k *= 2; // (4)
if(k == n)
return true; // (5)
return false;
- ( 1 ) (1) (1) 定义一个无符号整型 k k k；
- ( 2 ) (2) (2) 如果 n ≤ 0 n \\le 0 n≤0，则必然不是 2 的幂；
- ( 3 ) (3) (3) 1 必然是 2 的 0 次幂；
- ( 4 ) (4) (4) 枚举所有 2 的幂 2 2 2、 4 4 4、 8 8 8、… 、 2 31 2^31 231；
-
(
5
)
(5)
(5) 一旦找到一个和
n
n
n 相等，返回
true，则说明它是 2 的幂； -
(
6
)
(6)
(6) 最后，没有找到的话，返回
false表示不是 2 2 2 的幂；
2、3 的幂
实现一个函数
isPowerOfThree，判断一个 32位整型 n n n 是否是 3 的幂。
bool isPowerOfThree(int n)
int i;
unsigned int k = 1;
if(n <= 0)
return false;
if(n == 1)
return true;
for(i = 1; i <= 20; ++i) // (1)
k *= 3; // (2)
if(k == n)
return true;
return false;
和 2的幂 那一题相比，只改了两个地方：
- ( 1 ) (1) (1) 第一个是枚举的上限只需要到 20，因为 3 21 3^21 321 应该超过 32位 整型的上限了；
- ( 2 ) (2) (2) 第二个是每次枚举的是 1 1 1、 3 3 3、 9 9 9、…、 3 20 3^20 320，所以 k k k 不断乘 3。
3、4 的幂
实现一个函数
isPowerOfFour，判断一个 32位整型 n n n 是否是 4 的幂。
bool isPowerOfFour(int n)
int i;
unsigned int k = 1;
if(n <= 0)
return false;
if(n == 1)
return true;
for(i = 1; i <= 15; ++i) // (1)
k *= 4; // (2)
if(k == n)
return true;
return false;
和 3的幂 那一题相比，只改了两个地方：
- ( 1 ) (1) (1) 第一个是枚举的上限只需要到 15，因为 4 16 4^16 416 应该超过 32位 整型的上限了；
- ( 2 ) (2) (2) 第二个是每次枚举的是 1 1 1、 4 4 4、 16 16 16、…、 4 15 4^15 415，所以 k k k 不断乘 4。
4、n 的第 k 个因子
给你两个正整数 n n n 和 k k k 。如果正整数 i i i 满足
n % i == 0，那么我们就说正整数 i i i 是整数 n n n 的因子。考虑整数 n n n 的所有因子，将它们 升序排列 。请你返回第 k k k 个因子。如果 n n n 的因子数少于 k k k ，请你返回 − 1 -1 −1 。
int kthFactor(int n, int k)
int i;
int cnt = 0; // (1)
for(i = 1; i <= n; ++i) // (2)
if(n % i == 0) // (3)
++cnt;
if(cnt == k)
return i; // (4)
return -1; // (5)
-
(
1
)
(1)
(1) 定义一个计数器
cnt，初始化为 0； - ( 2 ) (2) (2) 枚举所有范围在 [ 1 , n ] [1, n] [1,n] 数，因为只有这些数才可能是 n n n 的因子；
-
(
3
)
(3)
(3) 一旦满足
n % i == 0，则计数器加一； - ( 4 ) (4) (4) 当计数器等于 k k k，则代表找到了 第 k k k 个因子，直接返回即可；
- ( 5 ) (5) (5) 如果一直没有找到，则表示不存在 第 k k k 个因子，返回 − 1 -1 −1；
5、有效的完全平方数
给定一个 正整数 x x x ，编写一个函数，如果 x x x 是一个完全平方数，则返回
true，否则返回false。
int 以上是关于《LeetCode零基础指南》(第三讲) 循环的主要内容，如果未能解决你的问题，请参考以下文章
《LeetCode零基础指南》(第十四讲) 力扣常见报错集锦
《LeetCode零基础指南》(第十一讲) 遇到不会的题怎么办？
[小玄的刷题日记]《LeetCode零基础指南》(第3讲) 循环