初级--05--- 取模运算转化为位运算位运算进行加减乘除

Posted 2021-12-18 高高for 循环

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

• 取模运算 转化为 位运算
• • 公式:
  • • • ==a%b = a&(b-1) ，且b=1<

---

取模运算 转化为 位运算

公式:

若满足b为2的整数次幂（即b=1<<k，k为整数）时，可用一个特殊的小技巧将取模运算转化为位运算，

a%b = a&(b-1) ，且b=1<<k（k为整数）

案例:

num % 64 等于 num & 63

原理:

注意:

取模的数b, 要满足b为2的整数次幂（即b=1<<k，k为整数）,公式转化才成立

位运算进行加减乘除

初级–01—二进制、位运算

num >> 6 相当于 num/64

1. 加法：add

1. 由a^b可得按位相加后没有进位的和；
2. 由a&b可得可以产生进位的地方；
3. 由(a&b)<<1得到进位后的值。
4. 那么 按位相加后原位和+进位和 就是加法的和了，而 a^b + (a&b)<<1 相当于把 +
   两边再代入上述三步进行加法计算。直到进位和为0说明没有进位了则此时原位和即所求和。

无进位信息和+进位信息和 = 加法的和

a^b + (a&b)<<1

	public static int add(int a, int b) 
		int sum = a;
		while (b != 0) 
			sum = a ^ b;    //无进位信息和
			b = (a & b) << 1;  //进位信息和
			a = sum;        //无进位相加信息
		
		return sum;
	

2. 减法: minus

可以将减法转换成加法计算。a - b = a + (-b)

相反数

正数相反数 = 其反码+1

	public static int negNum(int n) 
		return add(~n, 1);
	

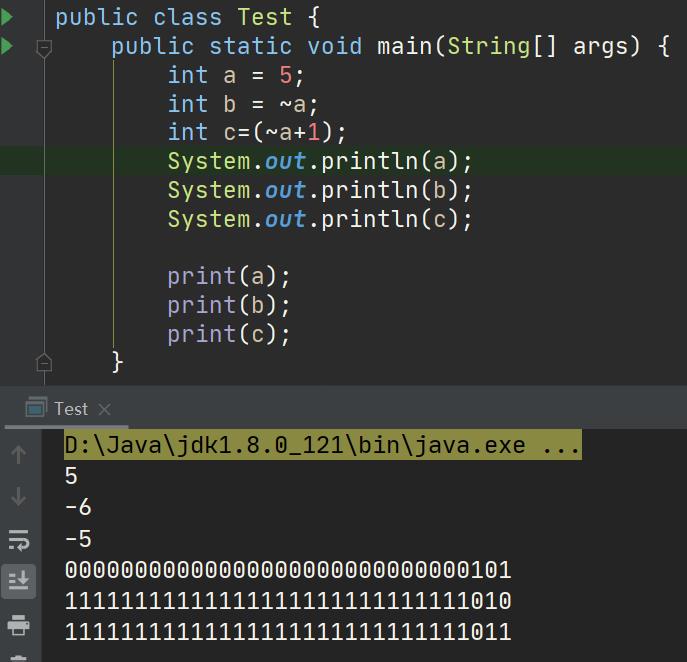
减法代码

public static int negNum(int n) 
		return add(~n, 1);
	

	public static int minus(int a, int b) 
		return add(a, negNum(b));
	

3. 乘法: multi

	public static int multi(int a, int b) 
		int res = 0;
		while (b != 0) 
			if ((b & 1) != 0) 
				res = add(res, a);
			
			a <<= 1;
			b >>>= 1;
		
		return res;
	

4. 除法: divide

除法的意义就在于：求a可以由多少个b组成。那么由此我们可得除法的实现：求a能减去多少个b，做减法的次数就是除法的商。

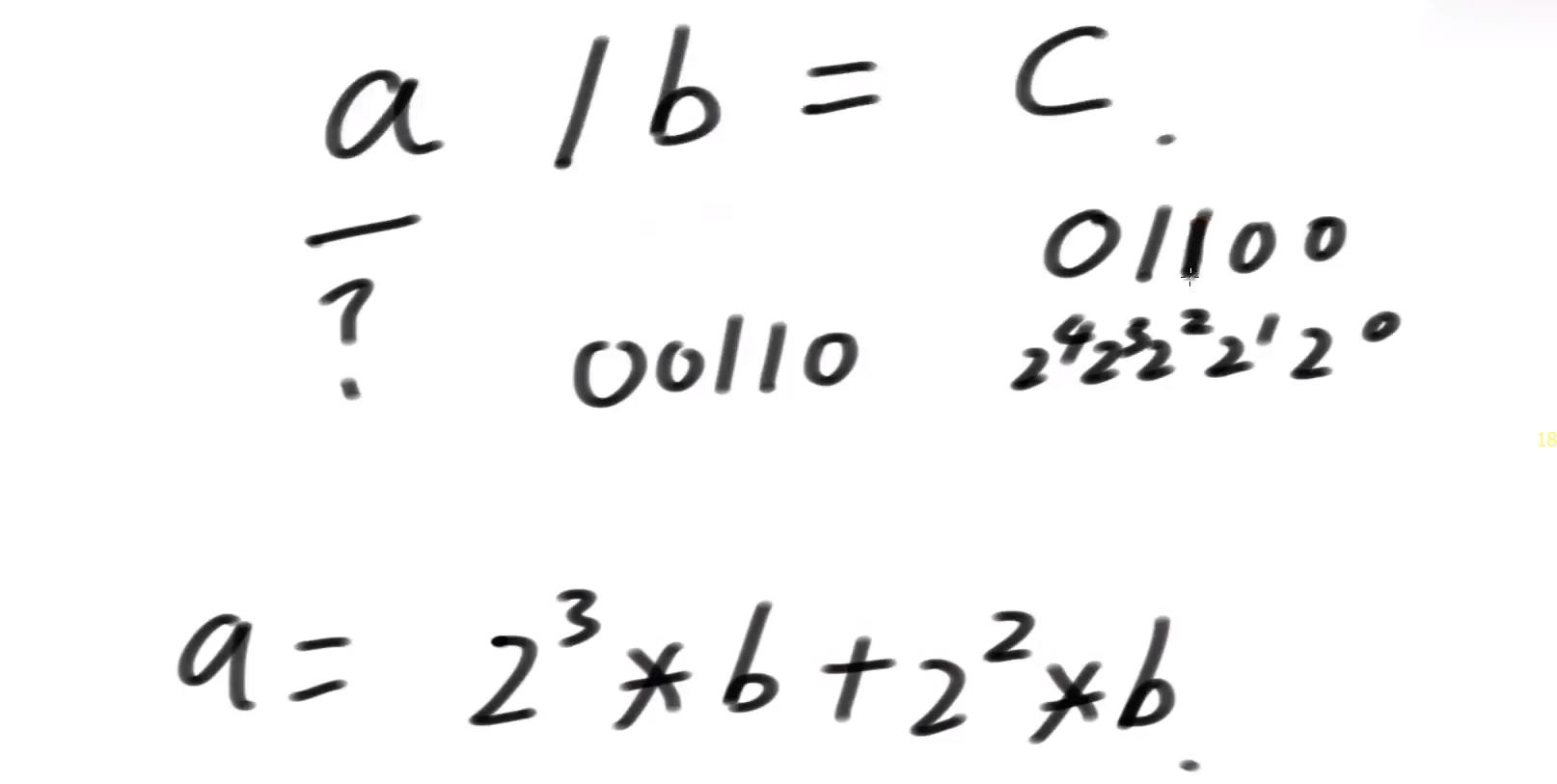
位运算–01—两数相除

public static boolean isNeg(int n) 
		return n < 0;
	

	public static int div(int a, int b) 
		int x = isNeg(a) ? negNum(a) : a;
		int y = isNeg(b) ? negNum(b) : b;
		int res = 0;
		for (int i = 30; i >= 0; i = minus(i, 1)) 
			if ((x >> i) >= y) 
				res |= (1 << i);
				x = minus(x, y << i);
			
		
		return isNeg(a) ^ isNeg(b) ? negNum(res) : res;
	

	public static int divide(int a, int b) 
		if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) 
			return 1;
		 else if (b == Integer.MIN_VALUE) 
			return 0;
		 else if (a == Integer.MIN_VALUE) 
			if (b == negNum(1)) 
				return Integer.MAX_VALUE;
			 else 
				int c = div(add(a, 1), b);
				return add(c, div(minus(a, multi(c, b)), b));
			
		 else 
			return div(a, b);