「SymPy」实战之Maxwell分布律分子最概然均方根与平均速率
Posted 行吟客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了「SymPy」实战之Maxwell分布律分子最概然均方根与平均速率相关的知识,希望对你有一定的参考价值。
目录

0 导言
Python之符号运算库SymPy的讲解系列已经包含了大部分常用的符号运算和推导方法,现在我们拿分子动理论——Maxwell平衡态速度分布律来练练手,巩固一下知识。本讲会用到以下知识,忘记的小伙伴可以先复习一下:
传送链接:
「SymPy」符号运算(1) 简介/符号/变量/函数/表达式/等式/不等式/运算符
「SymPy」符号运算(2) 各种形式输出、表达式的化简合并与展开
「SymPy」符号运算(3) (非)线性方程(组)求解、数列求和、连乘、求极限
1 Maxwell速度分布律
Maxwell于1859年推导出了分子速率的分布公式,后来Boltzmann用统计力学的方法也得到了相同的公式1 。对于做分子动理论和介观数值方法的工作者来说,Maxwell平衡态速度分布是相当重要的,掌握其推导、演变有利于深入理解气体动理学本质和拓展模型方法。话不多说,上公式:
f
(
v
)
=
4
π
(
m
2
π
k
T
)
1.5
exp
(
−
m
v
2
2
k
T
)
v
2
f(v) = 4\\pi\\left( \\dfracm2\\pi kT \\right)^1.5 \\exp\\left(\\dfrac-mv^22kT \\right) v^2
f(v)=4π(2πkTm)1.5exp(2kT−mv2)v2
Maxwell速率分布函数描述了气体分子关于速率的分布概率,
f
(
v
)
f(v)
f(v)可以看作数密度,
f
(
v
)
d
v
=
d
N
v
/
N
f(v)\\mathrm d v = \\mathrm d N_v / N
f(v)dv=dNv/N,其中分子速率
v
=
v
x
2
+
v
y
2
+
v
z
2
v = \\sqrtv_x^2 + v_y^2 + v_z^2
v=vx2+vy2+vz2,根据该速率分布函数,可以推导出分子的数学平均速率、均方根速率和最概然(最可几)速率,我们接下来就用Python的符号运算库SymPy进行推导。
先让大家看看输出效果(Anaconda→Jupyter编辑器)

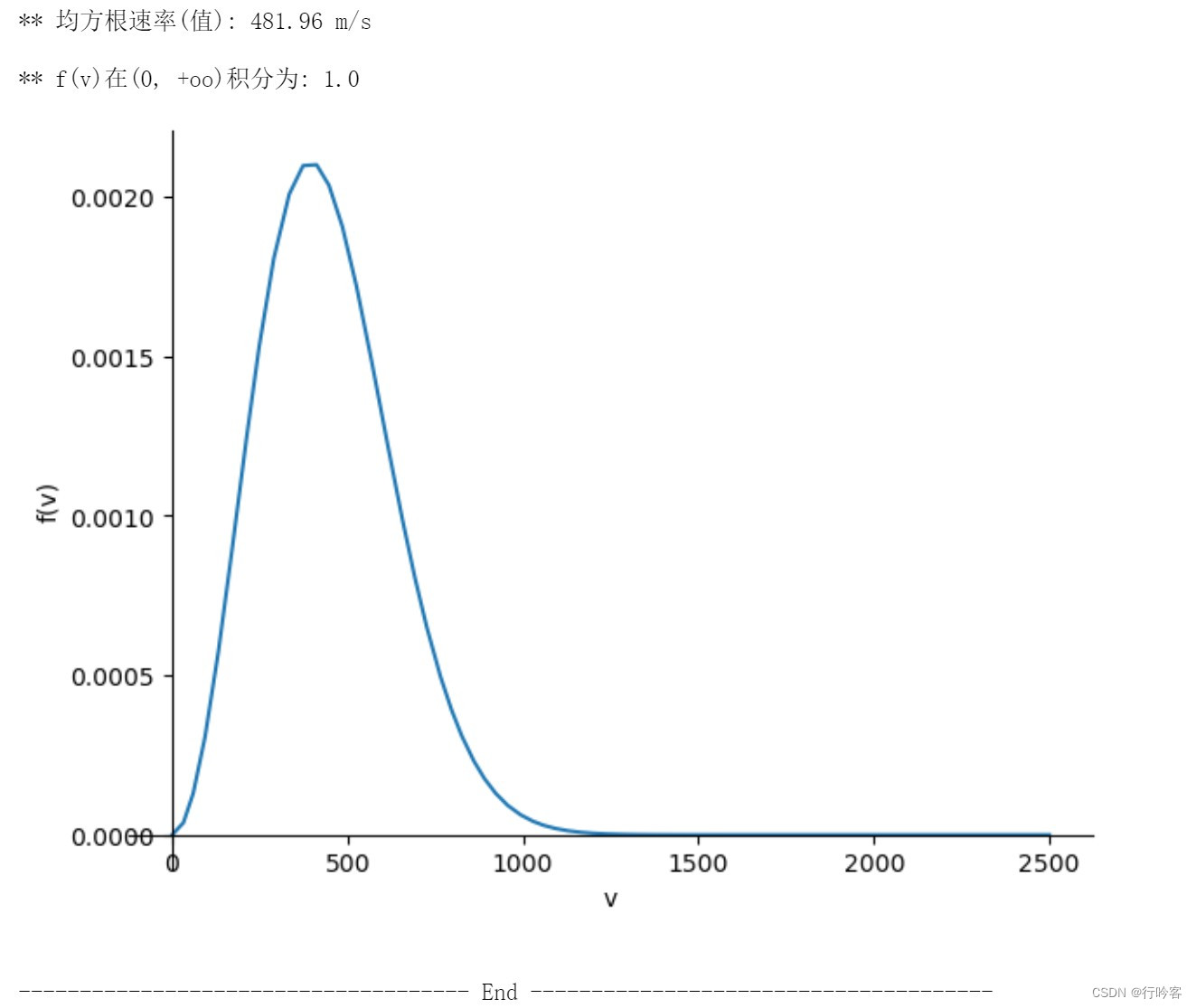
2 SymPy推导特征速度
2.1 导入库和方法
import sympy
from IPython.display import display, Math
from sympy.plotting import plot
from sympy import Rational, pi, pprint, oo
其中display函数是为了在控制台打印经过渲染后的
LaTeX
\\LaTeX
LATEX数学公式,如果无法正常使用的话可以直接使用SymPy的pprint()函数用字符串输出公式,效果会差一点。也可以使用print(sympy.latex(<expr>))打印输出
LaTeX
\\LaTeX
LATEX公式的源代码,放进支持
LaTeX
\\LaTeX
LATEX编译的编辑器中查看。
plot函数是SymPy内的函数绘图库,后端默认是以matplotlib库为基础的2,可以直接以符号作图,免去了离散数据的步骤,自动赋予坐标轴名称,但是功能相对简单,这里作演示用还是很方便的。
Rational之前没有讲过,该函数是获得有理数的方法,在计算过程中不会将这种有理数进行小数展开运算,使输出结果更简洁清晰。
2.2 初始化输出
sympy.init_printing()
可以根据控制台的背景优化SymPy输出的
LaTeX
\\LaTeX
LATEX渲染公式。
2.3 定义符号
## Define constants/variables
Av, kB = sympy.symbols('A_v k_B', positive = True)
T = sympy.symbols('T', positive = True)
m = sympy.symbols('m', positive = True) # molecular mass
v = sympy.symbols('v', positive = True) # \\sqrtv_x^2 + v_y^2 + v_z^2
M = 32 # Mole mass, take O2 (oxygen) for example
上面的代码定义了Avogadro常数、Boltzmann常数、温度、分子质量和速度的符号,并且对正负进行了限制。
代码以氧气分子举例,摩尔质量取 32 g / m o l 32\\mathrmg/mol 32g/mol。
2.4 设置符号替换
在演算过程中,我们既希望获得通用的符号表达式,又希望能过针对具体分子获得具体的值,这时定义一个符号与值的替换字典,结合SymPy表达式的.subs()函数,可以方便地做到这一点:
## Parameters substitution dict
subsdict = m: M / 6.02214076E+23 * 1E-3, # g -> kg
Av: 6.02214076E+23, # Avogadro constant
kB: 1.380649E-23, # Boltzmann constant
T: 298, # Temperature
这里定义了温度为 298 K 298\\mathrm K 298K。
2.5 定义分布律
直接给出Maxwell分布律,暂时不管分布律是怎么来的,先拿来用。
## Maxwell distribution
lam = m / (2 * kB * T)
f = 4*pi * (lam / pi)**Rational(1.5) * sympy.exp(- lam * v**2) * v**2
fs = f.subs(subsdict)
print("** Maxwell分布:")
# pprint(f) # 字符串显示模式
display(f) # 控制台渲染模式
pprint(f)和display(f)是两种输出方式,选用即可。
fs是根据刚才定义的符号与值的替换字典进行替换,只保留了未知的符号v。
输出结果:
2
m
3
2
v
2
e
−
m
v
2
2
T
k
B
π
T
3
2
k
B
3
2
\\frac\\sqrt2 m^\\frac32 v^2 e^- \\fracm v^22 T k_B\\sqrt\\pi T^\\frac32 k_B^\\frac32
πT23kB232m23v2e−2TkBmv2
结果比较清晰,但是SymPy不会根据指数的基进行自动合并。
值得一提的是,在之前讲指数式合并和化简时,提到了一个函数.powsimp(<expr>),它有一个参数设置combine = ‘base’,并且进行强制化简force = True时,会将指数相同的基进行合并:
a
b
c
b
=
(
a
c
)
b
a^bc^b = (ac)^b
abcb=(ac)b,但是现在这里加入了分式,表达式更加复杂,按基进行指数式合并不起作用(还会继续探索,有知道的大佬望不吝赐教)。
2.6 分布律作图
## Draw velocity distribution
p1 = plot(fs, (v, 0, 50), show = False)
p1.show()
绘制结果:

可以看到SymPy在符号绘图时,图片的采样密度比较低,这时可以通过设置plot里的参数adaptive = False, nb_of_points=500使之取消自适应采样,手动设置采样点数,曲线会更加光滑。
2.7 最概然速率
所谓最概然速率(最可几速率)就是在给定条件下分子最有可能出现的速率,或者一堆分子中速率相同的分子数最多的那个速率,就是求 v m v_m vm使 f ( v m ) = max f ( v ) f(v_m) = \\max\\f(v)\\ f(vm)=maxf(v),就是求 d f ( v ) / d v = 0 \\mathrm d f(v) / \\mathrm d v = 0 df(v)/dv=0的零点。
# most probable rate
vmst = sympy.solve(sympy.Eq(sympy.diff(f, v), 0), v)
print("\\n** 最概然速率(表达式): ")
# pprint(vmst[0])
display(vmst[0])
print(f"\\n** 最概然速率(值): vmst[0].subs(subsdict).n(5) m/s")
其中n.()函数表示控制输出的精度。
输出最概然速率的符号表达式:
2
T
k
B
m
\\frac\\sqrt2 \\sqrtT \\sqrtk_B\\sqrtm
m2TkB以上是关于「SymPy」实战之Maxwell分布律分子最概然均方根与平均速率的主要内容,如果未能解决你的问题,请参考以下文章