顺序查找的概念及实现代码详解
Posted 薛定谔的猫ovo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了顺序查找的概念及实现代码详解相关的知识,希望对你有一定的参考价值。
顺序查找的概念
顺序查找,又称为线性查找,主要用于在线性表中进行查找。
设若表中有n个元素,则顺序查找从线性表的先端开始,顺序用各元素的关键码值与给定值x进行比较,直到找到与其值相等的元素,则查找成功,给出该元素在表中的位置;若整个表检测完仍未找到与x相等的元素,则查找失败,给出失败信息。
顺序查找通常分为对一般的无序线性表的顺序查找和对按关键字有序的顺序表的顺序查找。
一般线性表的顺序查找(顺序表)
实现代码如下:
//动态分配顺序表的结构定义
#define InitSize 10 //定义线性表的初始长度
typedef struct
int *data; //指示动态分配数组的指针(其实就是int[]数组),注意0号单元留空
int maxsize, length; //数组的最大容量和当前长度
SeqList;
//顺序查找
int SeqSearch(SeqList &L, int x)
L.data[0] = x; //"哨兵"
int i;
for(i=L.length; L.data[i]!=x; i--); //从后往前查找
return i;
代码非常简单,在这里说一下“哨兵”的作用。为什么引入哨兵呢?
其实引入哨兵的目的是:使得循环不必判断数组是否越界,因为满足 i = = 0 i==0 i==0时,循环一定会跳出(表明查找失败),这样就提高了查找速度。
通俗来说,在这个算法中,哨兵就是待查值,将它放在查找方向的尽头,免去了每次比较后判断查找位置是否越界的操作。
那么对于这个算法,也可以不用提前预留出0号单元,而是在顺序表最后设置哨兵也是一样的。需要注意的是,存在L.data[L.length],即分配的数组最大空间大于数组的长度。
//顺序查找
int SeqSearch(SeqList &L, int x)
L.data[L.length] = x; //"哨兵"
int i=0;
while(L.data[i] != x)
i++; //从前往后查找
return i; //若表中不存在关键字为x的元素,则查找到i=L.length时退出循环
实际上,一切为了简化边界条件而引入的附加结点(或记录)均可称为哨兵,例如单链表中的头结点。
完整代码
#include<bits/stdc++.h>
using namespace std;
#define InitSize 10 //定义线性表的初始长度
typedef struct
int *data; //指示动态分配数组的指针(其实就是int[]数组),注意0号单元留空
int maxsize, length; //数组的最大容量和当前长度
SeqList;
//初始化
void InitList(SeqList &L)
L.length = 1; //0号单元留空,方便设置"哨兵"
L.maxsize = InitSize;
L.data = new int[InitSize];
//动态分配
void IncreaseSize(SeqList &L, int n)
int *p = L.data;
L.data = new int[L.maxsize + n];
for(int i=0; i<L.length; i++)
L.data[i] = p[i]; //将数据复制到新区域
L.maxsize += n;
free(p);
//插入操作:在顺序表L的第i个上插入x
void Insert(SeqList &L, int i, int x)
if(L.length >= L.maxsize) //自动增长10个长度
IncreaseSize(L,10);
for(int j=L.length; j>=i; j--)
L.data[j] = L.data[j-1];
L.data[i-1] = x;
L.length++;
//遍历表
void PrintList(SeqList L)
for(int i=1; i<L.length; i++) //0位置未赋值,故从1开始
cout<<L.data[i]<<" ";
cout<<endl;
//顺序查找
int SeqSearch(SeqList &L, int x)
L.data[0] = x; //"哨兵"
int i;
for(i=L.length; L.data[i]!=x; i--); //从后往前查找
return i; //若表中不存在关键字为x的元素,则查找到i=0时退出for循环
int main()
SeqList L;
InitList(L);
int n, x;
cin>>n;
for(int i=1; i<=n; i++)
cin>>x;
Insert(L, i+1, x); //留出第一个位置,也就是L.data[0]
cout<<endl;
cout<<"L:";
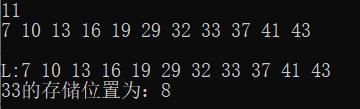
PrintList(L);
int res1 = SeqSearch(L, 33);
if(res1!=0)
cout<<"33的存储位置为:"<<res1<<endl;
else
cout<<"未找到该元素!"<<endl;
return 0;
关于顺序表的动态分配的操作可参考文章顺序表——动态分配顺序表上的基本操作(初始化、遍历、插入、查找、删除、判空等)
运行结果:
平均查找长度
若设顺序表中有n个元素,第
i
i
i个元素的查找概率为
p
i
p_i
pi,则查找到第
i
i
i个元素的比较次数为n-i+1(从后向前比较),那么查找成功的平均查找长度为:
A
S
L
成
功
=
∑
i
=
1
n
p
i
×
(
n
−
i
+
1
)
ASL_成功 = \\sum_i=1^n p_i × (n-i+1)
ASL成功=i=1∑npi×(n−i+1)
在查找概率相等时,即
p
=
1
n
\\ p=\\frac1n
p=n1 时,
A
S
L
成
功
=
∑
i
=
1
n
1
n
×
(
n
−
i
+
1
)
=
n
+
1
2
ASL_成功 = \\sum_i=1^n \\frac1n × (n-i+1) = \\fracn+12
ASL成功=i=1∑nn1×(n−i+1)=2n+1
查找不成功的比较次数为n+1次,从而顺序查找不成功的平均查找长度为
A
S
L
不
成
功
=
n
+
1
ASL_不成功 = n + 1
ASL不成功=n+1.
一般线性表的顺序查找(链表)
以单链表为例,其实现过程其实与顺序表大致相同。
在链表中使用查找指针沿着链表逐个结点检测,如果查找成功,则指针停留在链表中的某个结点;若整个链表都检查完但仍为发现满足要求的结点,则查找不成功,返回空地址。
实现代码如下:
//顺序查找
LNode *SeqSearch(LinkList L, int x)
LNode *p = L->next;
while(p!=NULL && p->data!=x)
p = p->next;
return p;
需要注意的是,循环中的两个条件顺序不能颠倒,只有在 p!=0 时 p->data 才是可取的。
前一个条件控制循环结束,取false时则查找失败;后一个条件判断是否找到,它取false时则查找成功。
完整代码
#include<bits/stdc++.h>
using namespace std;
typedef struct LNode
int data; //数据域
struct LNode *next; //指针域
LNode, *LinkList;
//初始化
void InitList(LinkList &L)
L = (LNode *)malloc(sizeof(LNode));
L->next = NULL;
//头插法建立单链表
LinkList HeadInsert(LinkList &L, int n)
InitList(L);
int x;
int i=0;
while(i<n)
cin>>x;
LNode *p = (LNode *)malloc(sizeof(LNode));
p->data = x;
p->next = L->next;
L->next = p;
i++;
return L;
//输出单链表中的结点值
void PrintLinkList(LinkList L)
LNode *p = L->next;
while(p!=NULL)
cout<<p->data<<" ";
p = p->next;
cout<<endl;
//顺序查找
LNode *SeqSearch(LinkList L, int x)
LNode *p = L->next;
while(p!=NULL && p->data!=x)
p = p->next;
return p;
int main()
LinkList L;
int n;
cin>>n;
HeadInsert(L, n);
cout<<endl;
cout<<"L:";
PrintLinkList(L);
LNode *p = SeqSearch(L, 33);
//通过输出后一个结点的结点值来验证是否找到了关键值为33的结点
if(p!=NULL)
cout<<"33的后一个结点值为:"<<p->next->data<<endl;
else
cout<<"未找到该元素!"<<endl;
return 0;
关于单链表的基本操作可参考文章单链表——单链表的定义及基本操作(初始化、头插法尾插法建表、查找、插入、删除、判空等)
运行结果为:

平均查找长度
对于单链表上的顺序查找算法的性能分析与顺序表相同,不再赘述,可参考上一部分。
顺序查找的优缺点
- 缺点:当n较大时,平均查找长度较大,效率低
- 优点:
- 对数据元素的存储没有要求,顺序存储和链式存储皆可。
- 对表中记录的有序性也没有要求,无论记录是否按照关键码有序,均可适用。
需要注意的是,对线性的链表只能进行顺序查找。
关键字有序的顺序表的顺序查找
如果顺序表里面的数据元素已经按照关键字码值从小到大排好序,则可以降低顺序查找的查找失败的平均查找长度,算法描述如下:
int OrderSeqSearch(SeqList &L, int x)
int i=0;
while(i<L.length && L.data[i]<x) //顺序比较
i++;
return (L.data[i]==x)? i : -1; //返回查找结果
一般用二叉判定树来描述顺序查找的查找过程,如下图所示:

平均查找长度
查找过程从根结点开始,查找成功时,查找指针一定停在某个圆形结点,树高 h=n ,其中n是元素个数。最大关键码的比较次数不超过h。
查找成功的平均查找长度在相等查找概率下等于:
A
S
L
成
功
=
1
n
×
∑
i
=
1
n
i
=
n
+
1
2
ASL_成功 = \\frac1n × \\sum_i=1^n i = \\fracn + 12
ASL成功=n1×i=1∑ni=2n+1
当查找不成功时,查找指针一定走到某个失败结点。
由于这些失败结点实际上就是空结点,指向它们的指针为空,所以到达失败结点的关键码的比较次数等于到达该失败结点前经过的圆形结点个数,也就是失败结点所在层次编号减1。
查找不成功的平均查找长度在相等查找概率下等于:
A
S
L
不
成
功
=
∑
i
=
1
n
q
i
×
(
l
i
−
1
)
=
1
n
+
1
×
(
1
+
2
+
.
.
.
+
n
+
n
)
=
n
2
+
n
n
+
1
ASL_不成功 = \\sum_i=1^n q_i × (l_i - 1) = \\frac1n + 1 × (1+2+...+n+n) = \\fracn2 + \\fracnn+1
ASL不成功=i=1∑