挑战程序设计竞赛（算法和数据结构）——8.3二叉树的表达的JAVA实现

Posted 2021-12-18 小乖乖的臭坏坏

题目：




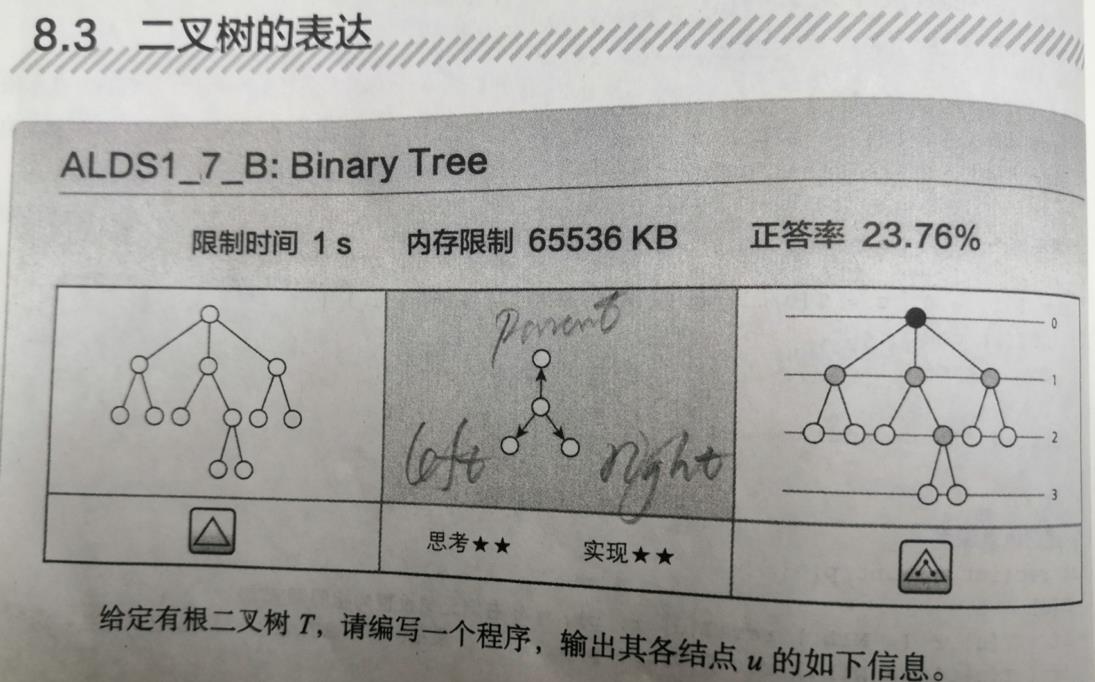
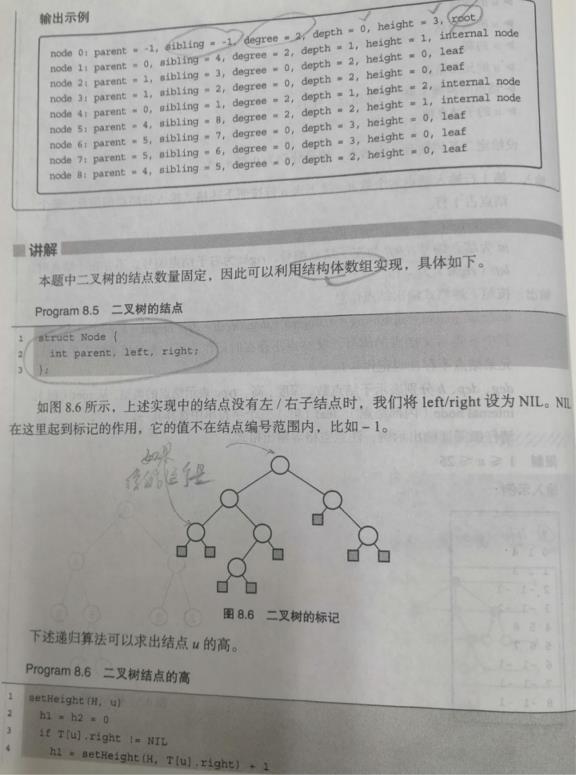
有了有根树这篇博文的代码基础，二叉树很快就能写出来，只要把左右节点指针进行改写即可！

https://blog.csdn.net/weixin_42887138/article/details/121472382

import java.io.BufferedInputStream;
import java.util.Scanner;

public class BinaryTree 
    public static class Node
        int parent, left, right;
        Node(int parent, int left, int right)
            this.parent = parent;
            this.left = left;
            this.right = right;
        
    

    public static void main(String[] args) 
        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        System.out.println("请输入树的节点数：");
        int n = cin.nextInt();
        Node[] T = new Node[10000];
        int[] H = new int[10000];
        int[] D = new int[10000];
        System.out.println("接下来，每行输入节点的编号id，度k，以及第1到第k个子节点的编号c1,c2...ck:");

        for(int i=0;i<n;i++) 
            T[i] = new Node(-1, -1, -1);//树节点的初始化
        
        //建立树型结构，定义节点联系
        for(int i=0;i<n;i++)
            int id = cin.nextInt();//输入节点编号
            int k = 2;//二叉树，度都为2
            int[] c = new int[k];//初始化子节点编号数组
            for(int j=0;j<k;j++)
                c[j] = cin.nextInt();
                if(c[j] == -1)continue;
                T[c[j]].parent = id;//树里面的每一个子节点的父节点都对应id
                if(j==0)T[id].left = c[j];//如果是第一个子节点，则赋值给父节点的左子节点
                if(j==1)T[id].right = c[j];//如果是第二个子节点，赋值给父节点的右子节点
            
        

        setDepth(T, D, 0, 0);
        setHeight(T, H, 0);

        for (int i=0;i<n;i++)
            System.out.print("node " + i + ": parent = " + T[i].parent + ", sibling = " + getSibling(T, i) + ", degree = " + getDegree(T, i) + ", depth = " + getDepth(T, i) + ", height = " + H[i]);
            printChildren(T, i);
            System.out.println();
        
    

    public static int getDegree(Node[] T, int u)
        int d = 0;
        if(T[u].left != -1)d++;
        if(T[u].right != -1)d++;
        return d;
    

    public static int getSibling(Node[] T, int u)
        if(T[u].parent!=-1)//有父节点，那很好办
            if(T[T[u].parent].left == u && T[T[u].parent].right != -1)
                return T[T[u].parent].right;
            
            if(T[T[u].parent].right == u && T[T[u].parent].left != -1)
                return T[T[u].parent].left;
            
        
        elsereturn -1;
        return -1;
    

    public static void setDepth(Node[] T, int[] D, int u, int p)
        if(u==-1)return;
        D[u] = p;
        setDepth(T, D, T[u].left, p+1);
        setDepth(T, D , T[u].right, p+1);
    

    public static int setHeight(Node[] T, int[] H, int u)
        int h1 = 0;
        int h2 = 0;
        if(T[u].right != -1)
            h1 = setHeight(T, H , T[u].right) + 1;
        
        if(T[u].left != -1)
            h2 = setHeight(T, H, T[u].left) + 1;
        
        return H[u] = Math.max(h1, h2);
    

    public static int getDepth(Node[] T, int u)
        int d = 0;
        while(T[u].parent != -1)
            u = T[u].parent;
            d++;
        
        return d;
    

    public static void printChildren(Node[] T, int u)
        if(T[u].left == -1 && T[u].right ==-1)
            System.out.print(", leaf");
        
        else//只要不是叶子节点，都应该有子节点的打印
            if(T[u].parent == -1)
                System.out.print(", root");
            //没有父节点，即自己是根节点
            else if(T[u].parent!=-1 && (T[u].left!=-1 || T[u].right!=-1))
                System.out.print(", internal node");
            //没有父节点和子节点
        
    

输入：

请输入树的节点数：
9
接下来，每行输入节点的编号id，度k，以及第1到第k个子节点的编号c1,c2...ck:
0 1 4
1 2 3
2 -1 -1
3 -1 -1
4 5 8
5 6 7
6 -1 -1
7 -1 -1
8 -1 -1

输出：

node 0: parent = -1, sibling = -1, degree = 2, depth = 0, height = 3, root
node 1: parent = 0, sibling = 4, degree = 2, depth = 1, height = 1, internal node
node 2: parent = 1, sibling = 3, degree = 0, depth = 2, height = 0, leaf
node 3: parent = 1, sibling = 2, degree = 0, depth = 2, height = 0, leaf
node 4: parent = 0, sibling = 1, degree = 2, depth = 1, height = 2, internal node
node 5: parent = 4, sibling = 8, degree = 2, depth = 2, height = 1, internal node
node 6: parent = 5, sibling = 7, degree = 0, depth = 3, height = 0, leaf
node 7: parent = 5, sibling = 6, degree = 0, depth = 3, height = 0, leaf
node 8: parent = 4, sibling = 5, degree = 0, depth = 2, height = 0, leaf