1126 Eulerian Path (25 分)难度: 一般 / 欧拉图的判定

Posted 2021-12-18 辉小歌

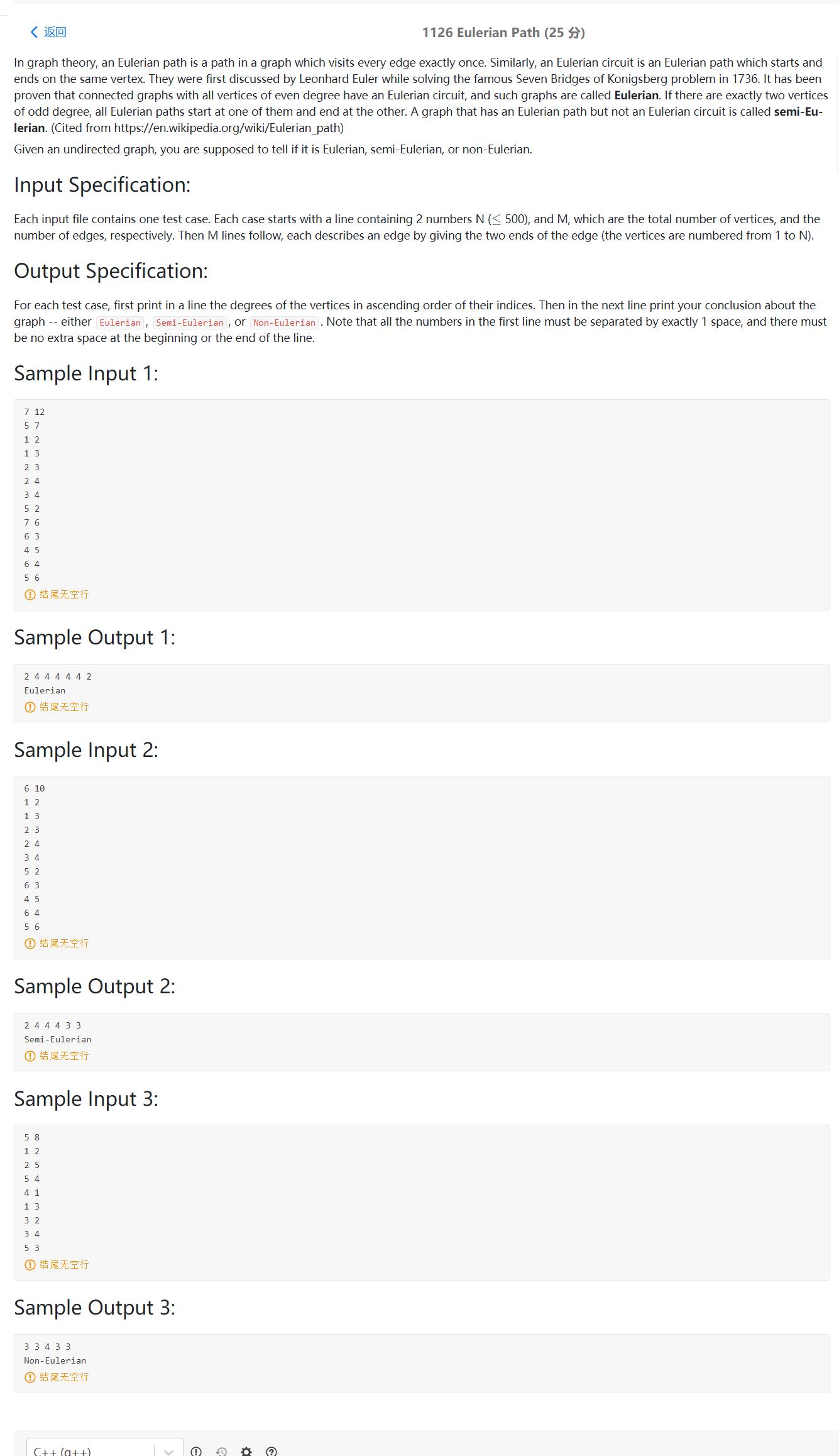
https://pintia.cn/problem-sets/994805342720868352/problems/994805349851185152
先判断图是否是联通的，可以用并查集，如果连通块的个数为1，那么就是联通的。
剩下的根据题意判断度数即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int d[N],p[N],n,m;
int cnt;
int find(int x)

    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];

int main(void)

    cin>>n>>m;
    int s=n;
    for(int i=1;i<=n;i++) p[i]=i;
    for(int i=0;i<m;i++)
    
        int a,b; cin>>a>>b;
        d[a]++,d[b]++;
        if(find(a)!=find(b)) p[find(a)]=find(b),s--;
    
    for(int i=1;i<=n;i++) 
    
        cout<<d[i];
        if(i!=n) cout<<" ";
        if(d[i]%2) cnt++;
    
    cout<<endl;
    if(!cnt&&s==1) puts("Eulerian");
    else if(cnt==2&&s==1) puts("Semi-Eulerian");
    else puts("Non-Eulerian");
    return 0;