[208]. 实现 Trie（前缀树）

Posted 2021-12-18 Debroon

实现 Trie（前缀树）

• • 题目
  • 函数原型
  • 字典树

 

---

题目

题目：https://leetcode-cn.com/problems/implement-trie-prefix-tree/

 

---

函数原型

class Trie 
public:
    Trie()   
    void insert(string word)  
    bool search(string word) 
    bool startsWith(string prefix) 
;

 

---

字典树

字典树，又名前缀树。

最大的特点在于，查询关键字和数据规模无关（单词越多查询越慢），只和查询的单词长度相关。

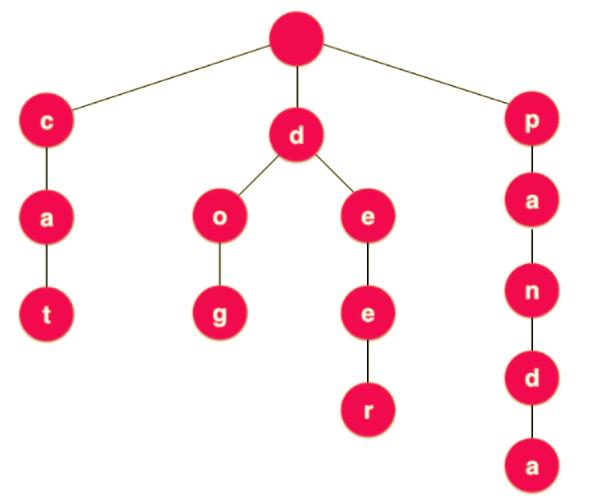
每个结点存放一个字母，从根节点开始遍历，遍历到尽头就是一个单词。

每个节点都有 N 个分支，单纯英文字母是 26 个，如果包含大小写，是 52 个，如果包含特殊字符是 256 个

#define N 26
class Node 
	char c;
	Node *next[N];         // 指针数组，数组中存放的是指针，默认为NULL

• 这句话有漏洞：每个结点存放一个字母，从根节点开始遍历，遍历到尽头就是一个单词。

一个英文单词可能是另一个英文单词的前缀，如 Pan（平底锅🍳）是 Panda（熊猫） 的前缀。

正因为如此，我们需要一个标识，代表是否是一个单词的结尾。

#define N 26
class Node 
	char c;
	bool isEnd;
	Node *next[N];         // 指针数组，数组中存放的是指针，默认为NULL

一般 Trie 实现就是如此，但一些人发现不用 成员c 节点储存的英文字母 也可以：

#define N 26
class Node 
    int size;              // 记录字典树单词数量
	bool isEnd;
	Node *next[N];         // 指针数组，数组中存放的是指针，默认为NULL

我也没搞懂，怎么去掉一个成员也可以，先占个位，以后搞懂了再补。

好，我们用 Trie 来解决 208。

class Trie 
private:
    vector<Trie*> next;   // 指针数组，数组中存放的是指针，默认为 nullptr
    bool isEnd;
    int size;             // 记录字典树单词数量，这题不需要这个，其实也可以省掉                    

public:
    Trie() : next(26), isEnd(false), size(0) 

	// 向 Trie 中添加一个新的单词
    void insert(string word) 
        Trie* root = this;                     // 声明一个变量，初始的时候在 root 位置
        for (char c : word)                   // 每次取出一个字符
            c -= 'a';                          // 一个单词可能另一个单词的前缀，避免重复创建
            if (root->next[c] == nullptr)      // 检查节点的孩子节点是否存在字母 c 这个结点
                root->next[c] = new Trie();    // 不重复，才创建
            root = root->next[c];              // 如果已经存在，就直接走到孩子结点
        
        
        if( root->isEnd == false )            // 避免重复添加
        	root->isEnd = true;                // 直到 root 来到最后一个字符，表示添加完毕
        	size ++;                           // 单词数+1
        
    

	// 通用查询：支持普通查询和前缀查询，因为一个单词就是一个单词的前缀，查找思路、代码不变
	// 查找的整体逻辑和添加逻辑一致，唯一不同的地方在于 --- 没有这个字符时，从添加结点改成直接返回 false
    Trie* searchPrefix(string prefix) 
        Trie* root = this;
        for (char c : prefix) 
            c -= 'a';
            if (root->next[c] == nullptr)
                return nullptr;              // 单词不存在 false
            root = root->next[c];
        
        return root;
    

	/* 查看 Trie 是否包含某个单词
	   - 整体逻辑和添加逻辑一致，唯一不同的地方在于 --- 没有这个字符时，从添加结点改成直接返回 false
	   - 一直查下去，直到最后一个字符，但我们不能直接返回 true
	   - 如字典有 panda，但没 pan，我们查 pan 应该为 false，那表现就在 root->isEnd == false
	   - root->isEnd == true 才算有这个单词，否则虽然遍历到了 pan，但 Trie 中依然没有这个单词
	*/ 
    bool search(string word) 
        Trie* root = this->searchPrefix(word);            // 调用通用查询
        return root != nullptr && root->isEnd;
    

	// 前缀查询：查询是否有单词以 prefix 为前缀
    bool startsWith(string prefix) 
        return this->searchPrefix(prefix) != nullptr;     // 调用通用查询
    
;