Java 求解平衡二叉树

Posted 2021-12-18 南淮北安

文章目录

• • 一、题目
  • 二、题目分析
  • 三、迭代法
  • 四、总结

一、题目

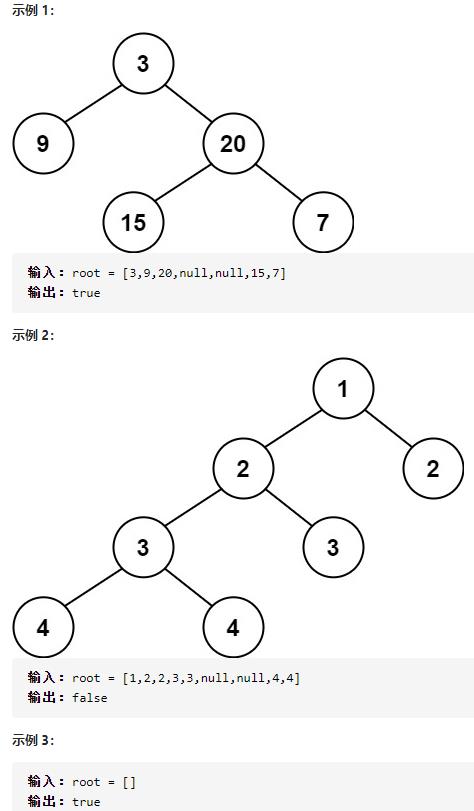
给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

二、题目分析

该题和求解二叉树的最大深度有很大区别：

二叉树节点的深度：指从根节点到该节点的最长的简单路径边的条数
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数

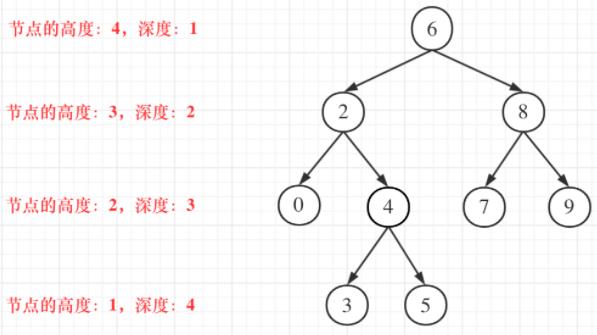
高度和深度的计算方法以 LeetCode 为准，即以节点为一度

深度可以从上到下去查，所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

求解二叉树的最大深度，实际用了后序遍历，原因是把求解二叉树的最大深度，看作了求解二叉树根的高度

该题，需要判断左右子树的高度值之差是否大于1，所以本质是后序遍历

三、迭代法

（1）确定递归参数及返回值

参数：二叉树节点，返回值：二叉树节点的高度

（2）确定递归终止条件

当该节点为空时，返回0，表示该节点的高度为0

（3）确定递归逻辑

后序遍历

class Solution 
    public boolean isBalanced(TreeNode root) 
        return getDepth(root) == -1 ? false : true;
    

    public int getDepth(TreeNode node) 
        //递归终止
        if (node == null) 
            return 0;
        
        //递归遍历左子树的高度
        int leftDepth = getDepth(node.left);
        //出现-1，表示没必要继续
        if (leftDepth == -1) 
            return -1;
        
        //递归遍历右子树的高度
        int rightDepth = getDepth(node.right);
        //出现-1，表示没必要继续
        if (rightDepth == -1) 
            return -1;
        
        //判断左右子树高度值只差是否大于1
        return Math.abs(leftDepth - rightDepth) > 1 ? -1 : 1 + Math.max(leftDepth, rightDepth);
    

四、总结

该题使用递归法较为简单，使用迭代法就有点复杂了

注意高度和深度的区别：

二叉树节点的深度：指从根节点到该节点的最长的简单路径边的条数
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数