LeetCode 150. 逆波兰表达式求值

Posted 2021-12-18 数据结构和算法

问题描述

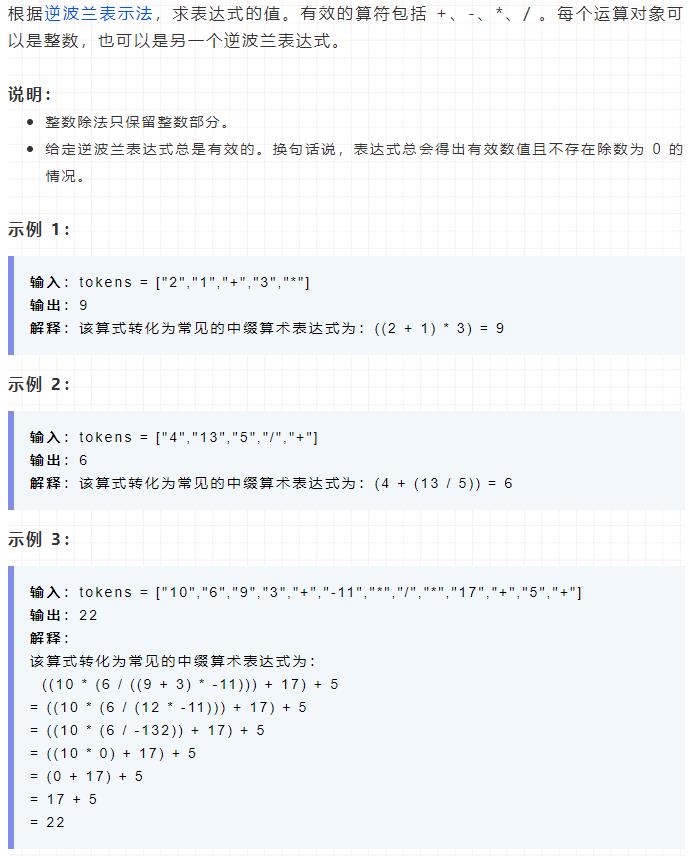
对于逆波兰表达式维基百科上是这样描述的：逆波兰表示法（Reverse Polish notation，RPN，或逆波兰记法），是一种是由波兰数学家扬·武卡谢维奇1920年引入的数学表达式形式，在逆波兰记法中，所有操作符置于操作数的后面，因此也被称为后缀表示法。逆波兰记法不需要括号来标识操作符的优先级。

逆波兰记法中，操作符置于操作数的后面。例如表达“三加四”时，写作“3 4 + ”，而不是“3 + 4”。如果有多个操作符，操作符置于第二个操作数的后面，所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作“3 4 - 5 + ”：先3减去4，再加上5。使用逆波兰记法的一个好处是不需要使用括号。例如中缀记法中“3 - 4 * 5”与“（3 - 4）*5”不相同，但后缀记法中前者写做“3 4 5 * - ”，无歧义地表示“3 (4 5 *) -”；后者写做“3 4 - 5 * ”。

逆波兰表达式的解释器一般是基于堆栈的。解释过程一般是：操作数入栈；遇到操作符时，操作数出栈，求值，将结果入栈；当一遍后，栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现，并且能很快求值。

注意：逆波兰记法并不是简单的波兰表达式的反转。因为对于不满足交换律的操作符，它的操作数写法仍然是常规顺序，如，波兰记法“/ 6 3”的逆波兰记法是“6 3 /”而不是“3 6 /”；数字的数位写法也是常规顺序。

以上内容来自于维基百科。如果你能明白什么是逆波兰表达式，那么对于这道题基本上没有什么难度，我们只需要使用一个栈即可解决。这里我们先不看代码，我们简单介绍一下算术表达式的几种表示方式。

中序法

<操作数><运算符><操作数>

例如 1+2，5*7，这种是最常见的，也是大家习惯的写法。由于括号以及运算符优先级的问题，这种在计算机中不太好运算，一般不太使用。

前序法

<运算符><操作数><操作数>

例如 中序表达式的3+4，在前序表达式中则为+3 4。

3\\*4+6\\*9则表示为+\\*3 4\\*6 9（注意这里数字之间都有空格）

后序法

<操作数><操作数><运算符>

例如 前序表达式中的3+4，在后续表达式中为3 4+。

3*4+6*9则表示为3 4*6 9*+

我们可以看到前中后三种表示法是根据运算符的位置来决定的。这里就不在过多介绍，后续我抽时间在单独讲，以及这三种表达式的相互转换。

通过上面的简单介绍，我们知道逆波兰表达式其实就是算术表达式的后续法。我们遍历字符串数组，如果是数字就把他们压栈，如果是运算符，就从栈中连续弹出两个数字进行运算，运算完之后再把结果放到栈中。原理比较简单，看下代码。

public int evalRPN(String[] tokens) 
    Stack<Integer> stack = new Stack<>();
    //遍历字符串数组
    for (String token : tokens) 
        //如果是运算符，就从栈中连续弹出两个数字，
        //让他们运算，然后把运算结果放到栈中
        if (token.equals("+")) //加法
            int num1 = stack.pop();
            int num2 = stack.pop();
            stack.push(num2 + num1);
         else if (token.equals("-")) //减法
            int num1 = stack.pop();
            int num2 = stack.pop();
            stack.push(num2 - num1);
         else if (token.equals("*")) //乘法
            int num1 = stack.pop();
            int num2 = stack.pop();
            stack.push(num2 * num1);
         else if (token.equals("/")) //除法
            int num1 = stack.pop();
            int num2 = stack.pop();
            stack.push(num2 / num1);
         else 
            //如果是数字，就把他压入到栈中
            stack.push(Integer.parseInt(token));
        
    
    //最后栈中只有一个元素，取出即可
    return stack.pop();