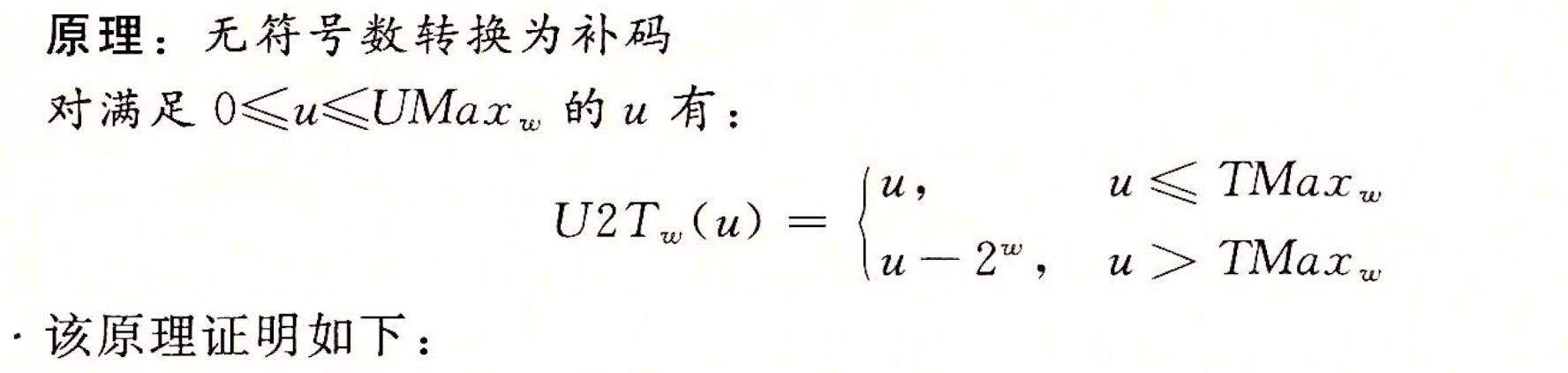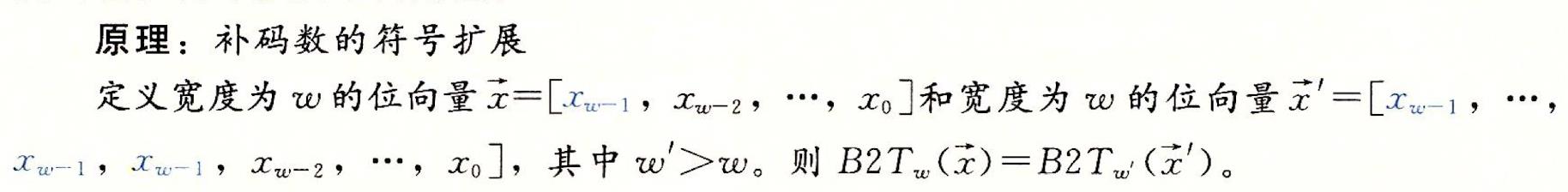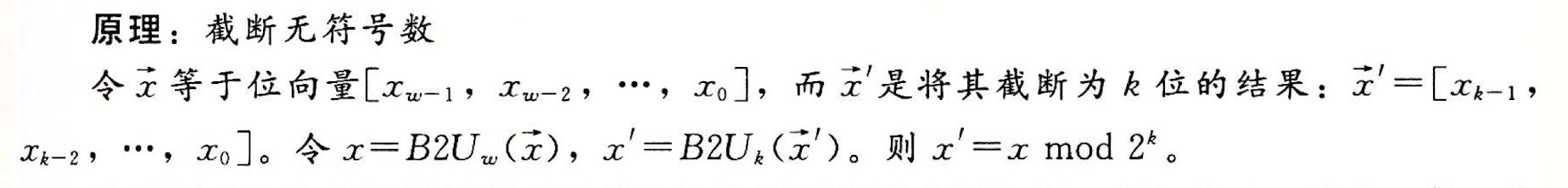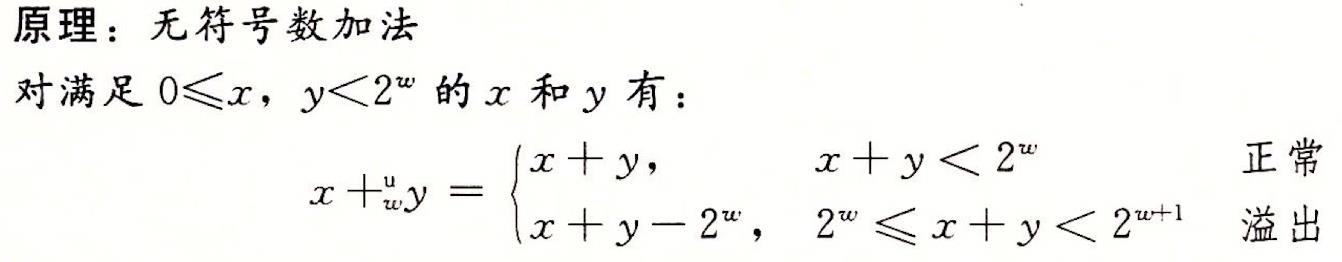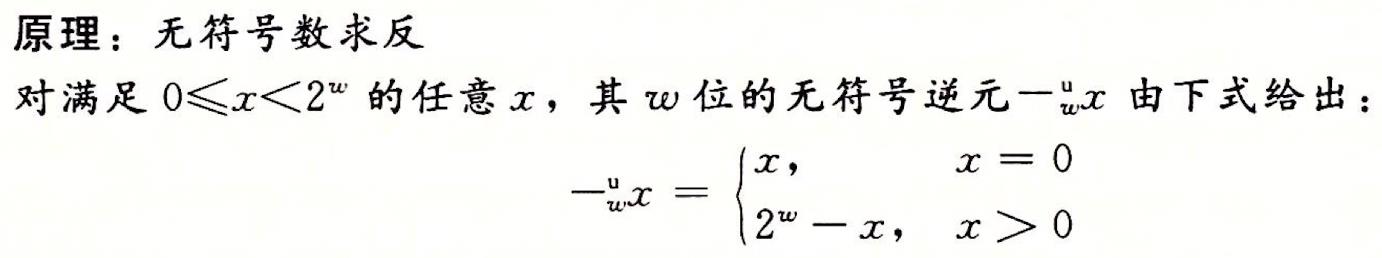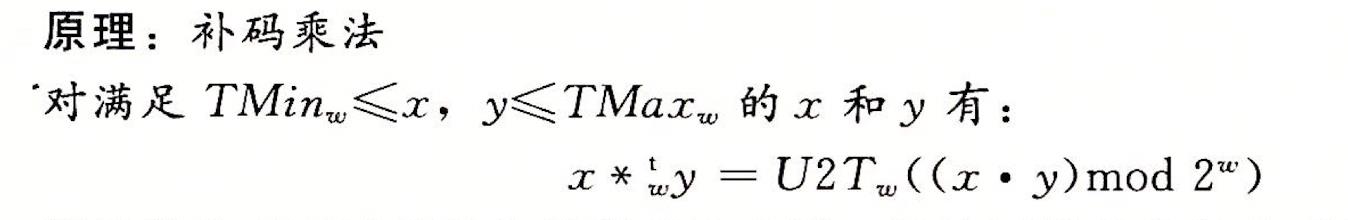《深入理解计算机系统》·深度挖掘第2章·第二话
Posted kikokingzz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《深入理解计算机系统》·深度挖掘第2章·第二话相关的知识,希望对你有一定的参考价值。
🌕写在前面
- 🍊博客主页:kikoking的江湖背景
- 🎉欢迎关注🔎点赞👍收藏⭐️留言📝
- 🌟本文由 kikokingzz 原创,CSDN首发!
- 📆首发时间:🌹2021年11月22日🌹
- 🆕最新更新时间:🎄2021年11月22日🎄
- ✉️坚持和努力一定能换来诗与远方!
- 📠参考书籍:📚《深入理解计算机系统》
- 🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢感谢感谢!
- 《深入理解计算机系统》·深入浅出·快速理解第2章·第一话
目录
🔥2.2.2·无符号数编码
✨✨✨我是分割线✨✨✨
🔥2.2.3·补码编码
✨✨✨我是分割线✨✨✨
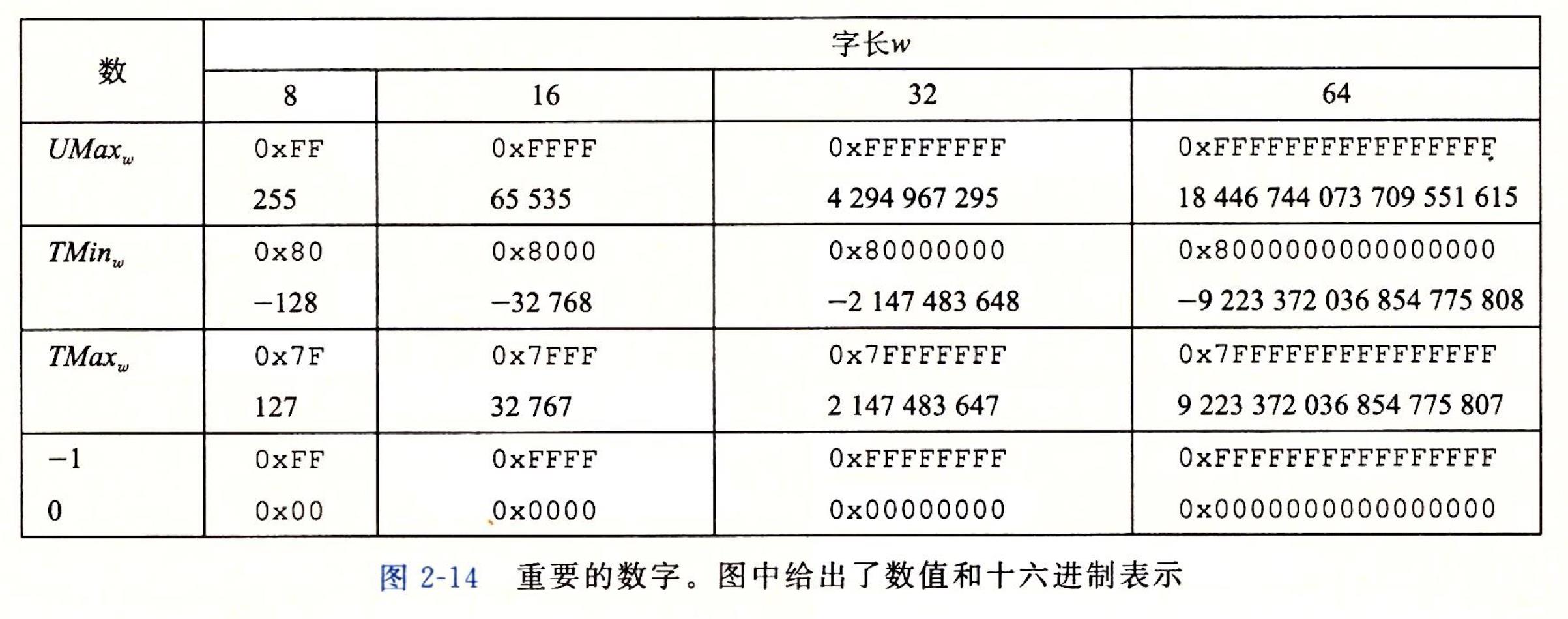
⚡️背诵表格
✨✨✨我是分割线✨✨✨
🔥2.2.4·有符号数和无符号数之间的转换
🍊1.强制类型转换----转换位的解释方式
·强制类型转换不改变位的值,只改变解释位的方式(B2T解释/B2U解释)
·-12345的16位补码(B2T)与53191的16位无符号表示(B2U)是一样的
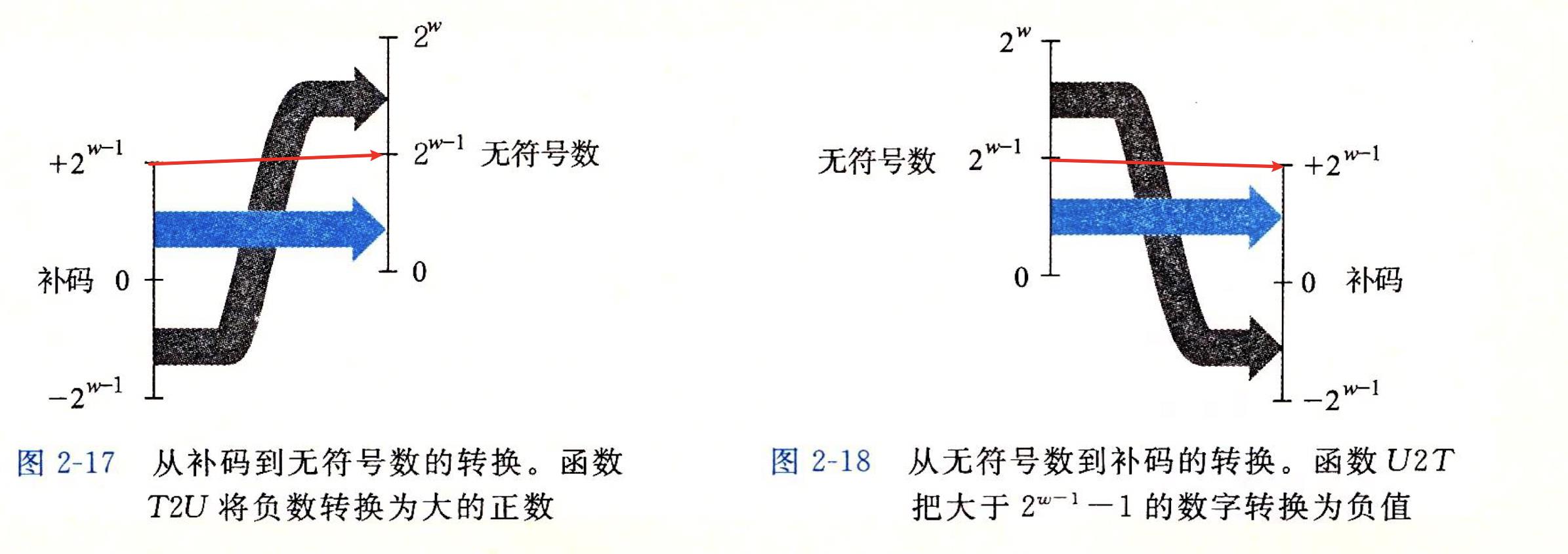
·通过图来解释,就是掌握下图,所有转换问题都可以得到解决:
🍊2.补码转换为无符号数
🍊3.无符号数转换为补码
✨✨✨我是分割线✨✨✨
🔥2.2.5·C语言中的有符号数与无符号数
🍊1.强制转换与隐式转换
上下两种方式结果一样
🍊2.有符号数(补码)和无符号数的转换输出
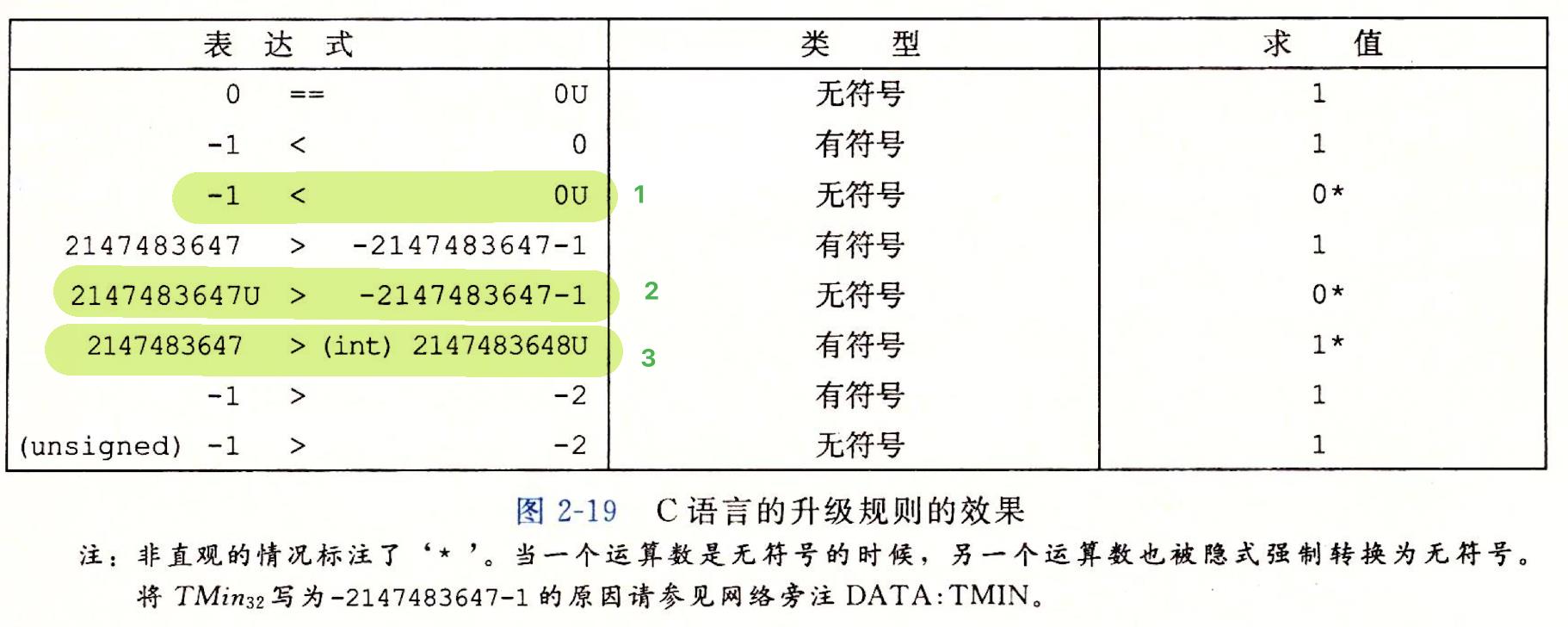
🍊3.无符号数与有符号数运算
·执行运算时,如果它的运算数一个是有符号的而另一个是无符号的,那么C语言会隐式地将有符号参数强制类型类型转换为无符号数
✨✨✨我是分割线✨✨✨
🔥2.2.6·扩展一个数字的位表示
1.无符号数的零扩展
·将无符号数转换为一个更大的数据类型,我们只要简单地在表示的开头添加0
2.补码数的符号扩展
·位向量[101]表示值-4+1= -3;对它应用符号扩展,得到位向量[1101], 表示的值 -8+4+1=-3;我们可以看到, 对于w=4, 最高两位的组合值是 -8+4=-4, 与w=3时符号位的值相同;类似地,位向量[111]和[1111]都表示值一1。
3.典型案例
案例1·有符号无符号的扩展
案例2·有符号无符号与扩展同时进行
·应当先扩展(改变大小),再符号转换
✨✨✨我是分割线✨✨✨
🔥2.2.7·截断数字
1.截断无符号数
2.截断补码数值
·先对其进行截断无符号数操作,然后再U2T(无符号数转补码)
3.例题
✨✨✨我是分割线✨✨✨
🔥2.2.8·有符号数与无符号数的优质例题
例题1:考察无符号与有符号数转换
例题2:考察无符号与有符号数转换
✨✨✨我是分割线✨✨✨
🔥2.3.1·无符号加法
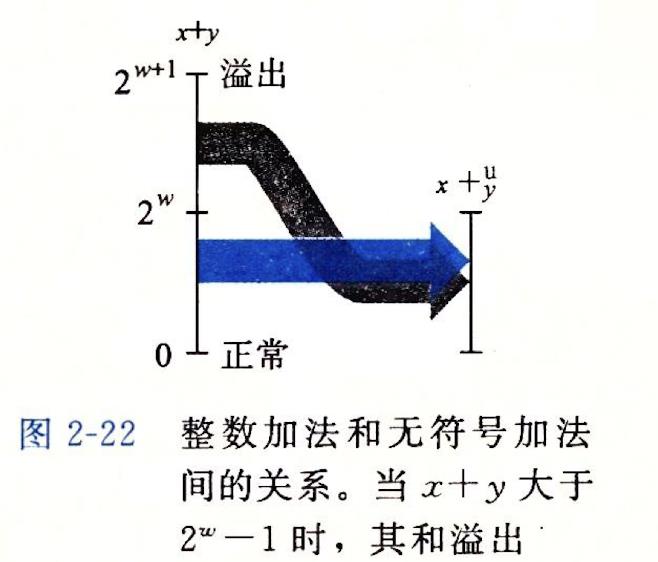
🍊1.无符号数加法
🍊2.检测无符号数加法中的溢出
🍊3.无符号数求反
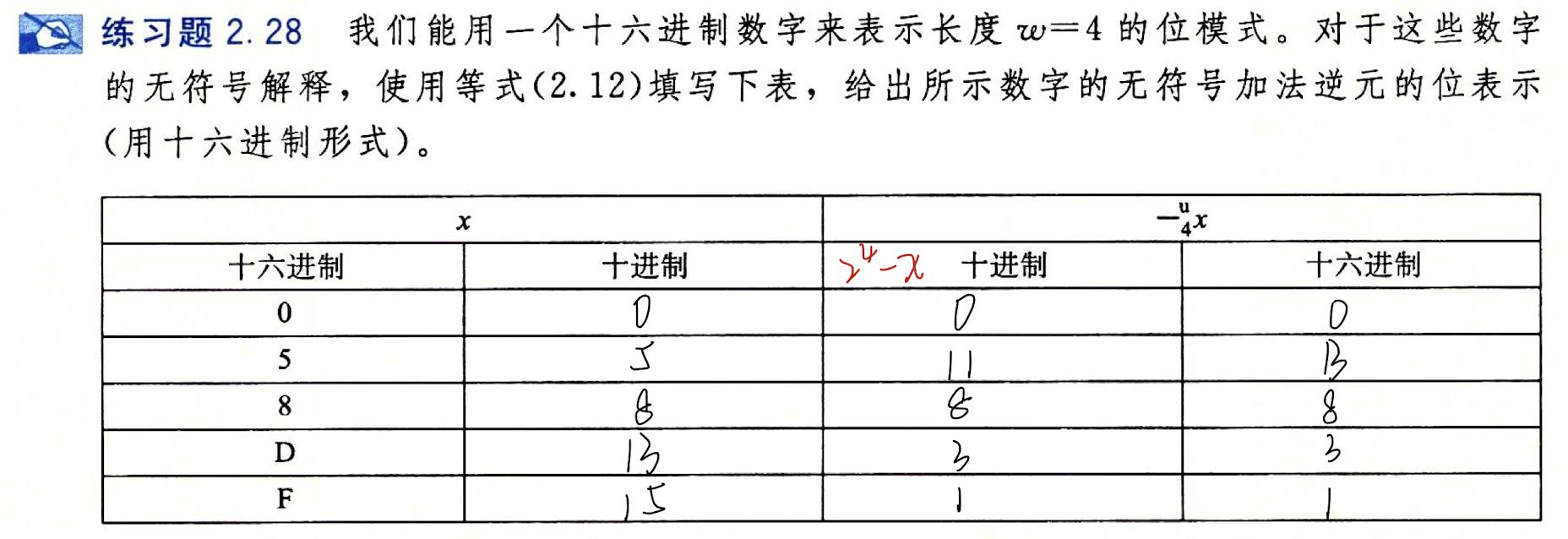
🍊4.习题
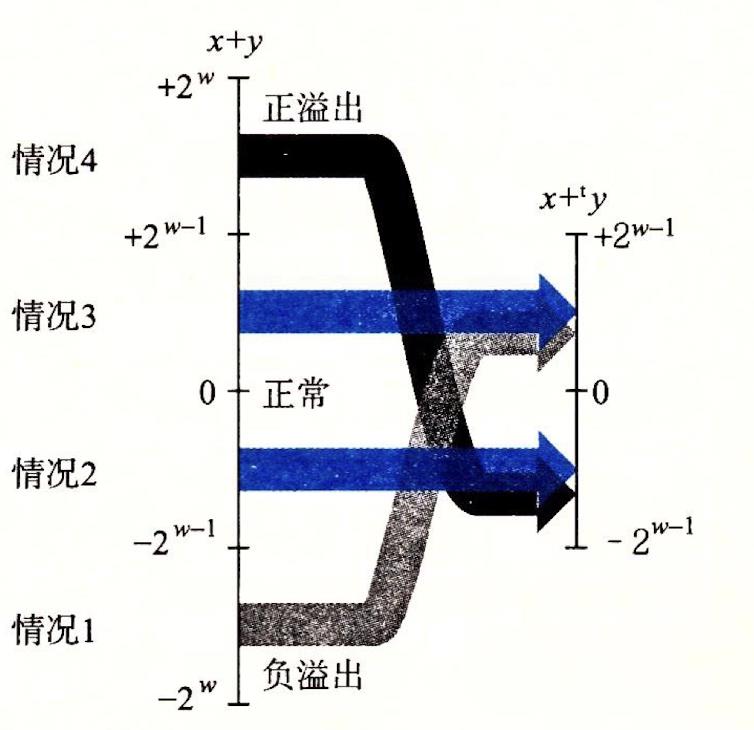
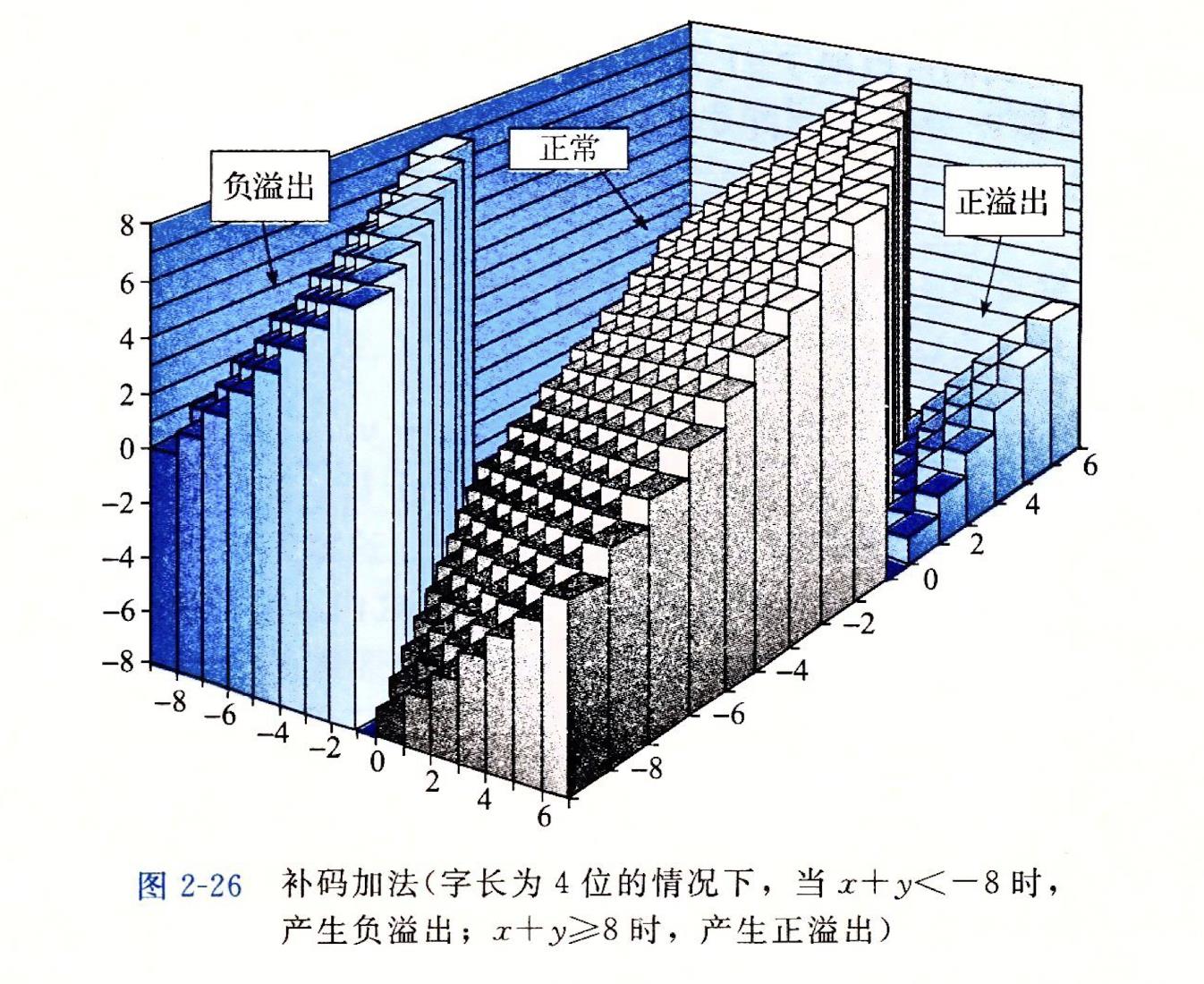
🔥2.3.2·补码加法
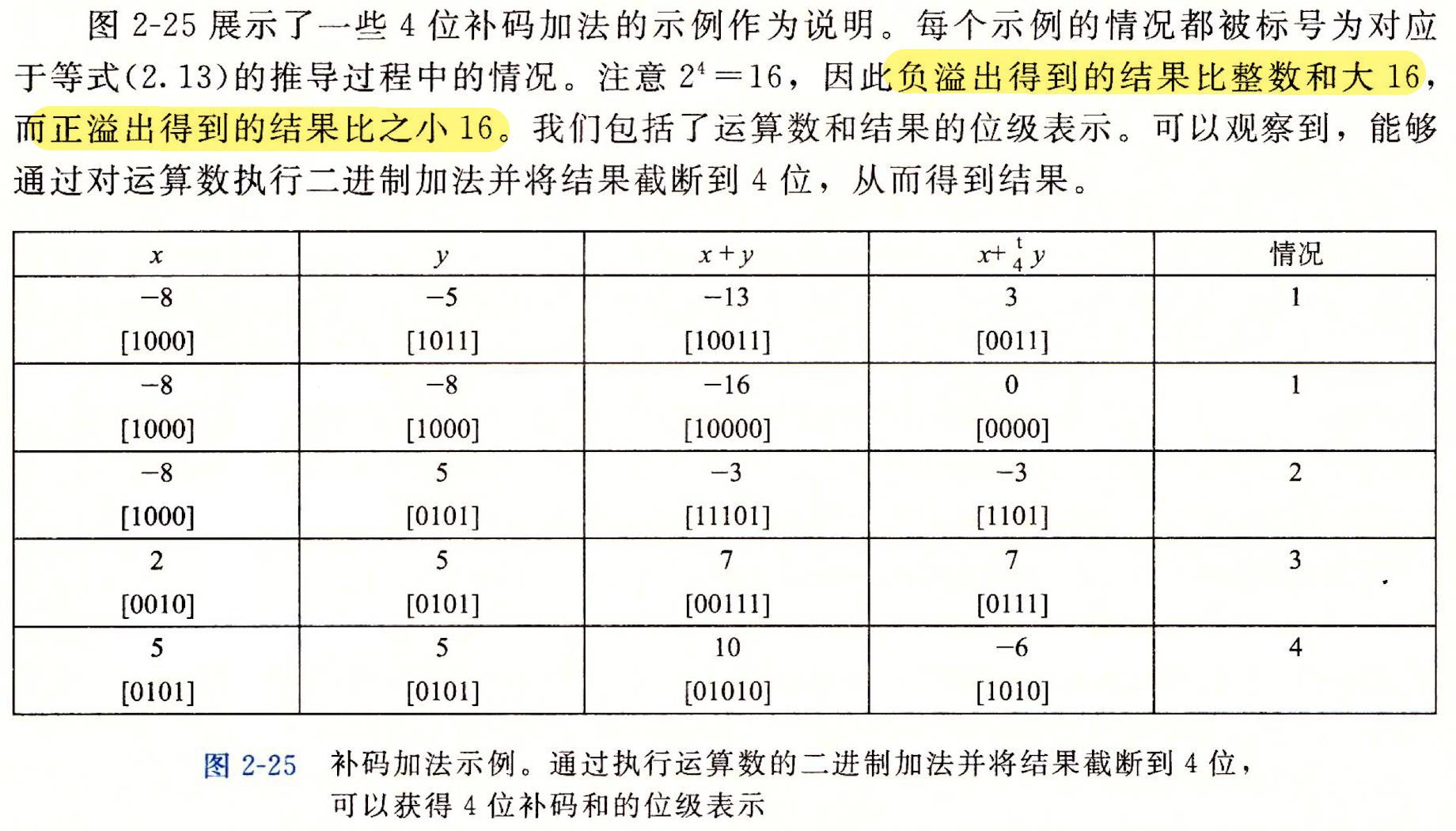
🍊1.补码的加法
🍊2.检测补码加法中的溢出
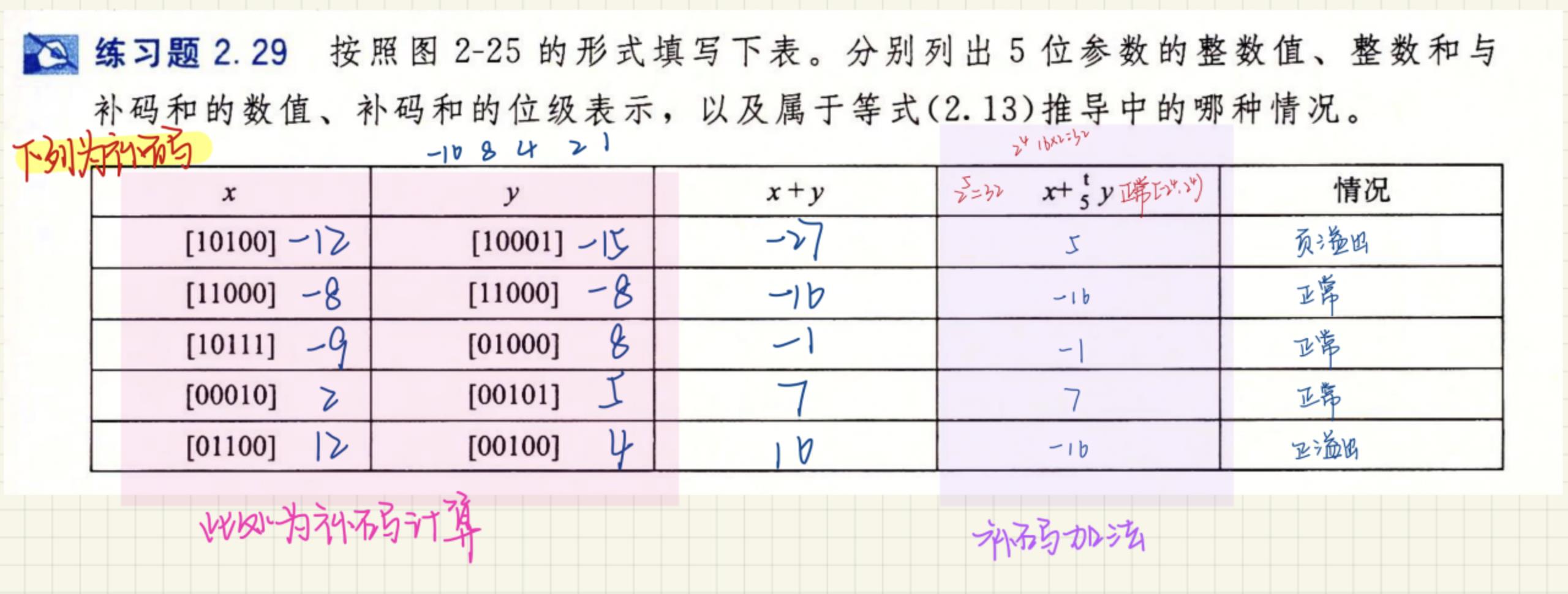
🍊3.优质习题
✨✨✨我是分割线✨✨✨
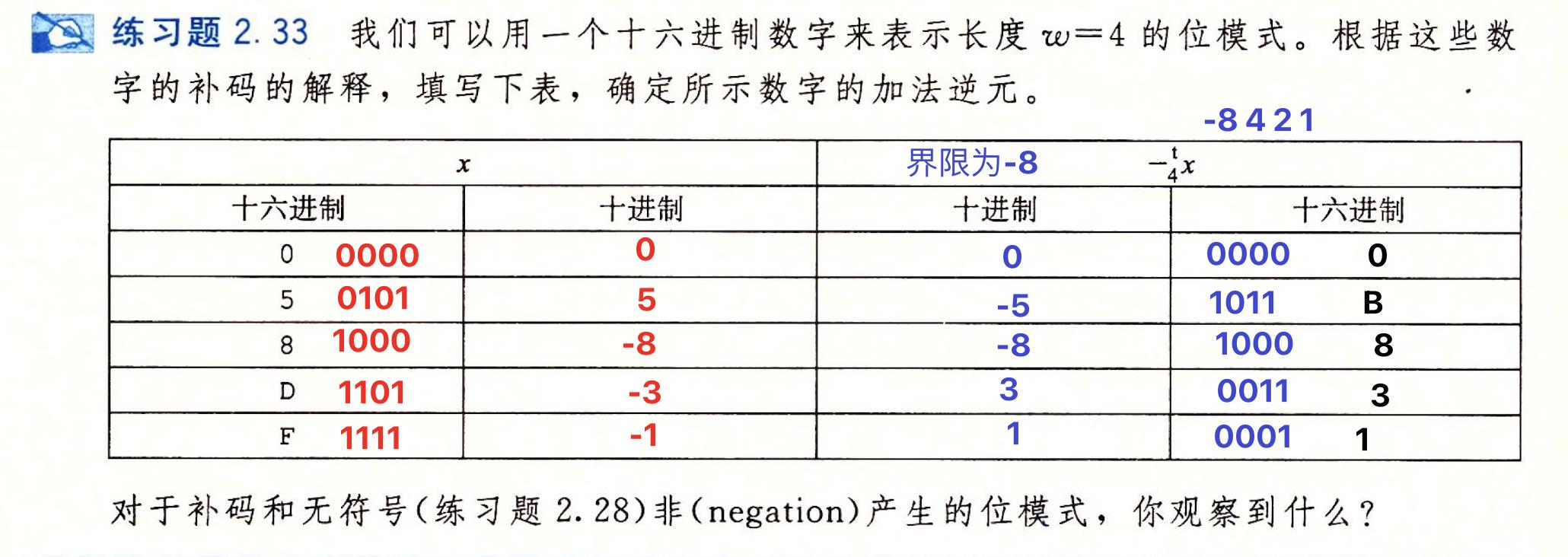
🔥2.3.3·补码的非
🍊1.补码的非
·最小值的非为本身;其余都是相反数
🍊优质习题
✨✨✨我是分割线✨✨✨
🔥2.3.4·无符号数乘法
✨✨✨我是分割线✨✨✨
🔥2.3.5·补码乘法
🍊1.补码乘法
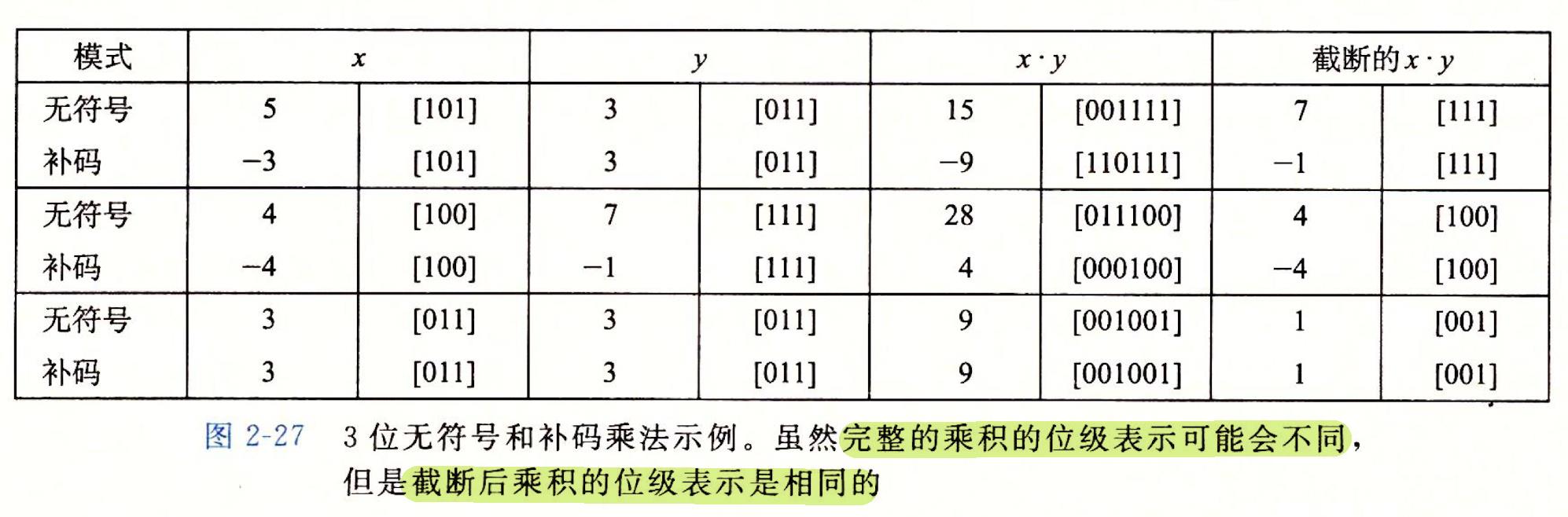
🍊2.无符号和补码乘法的位级等价性
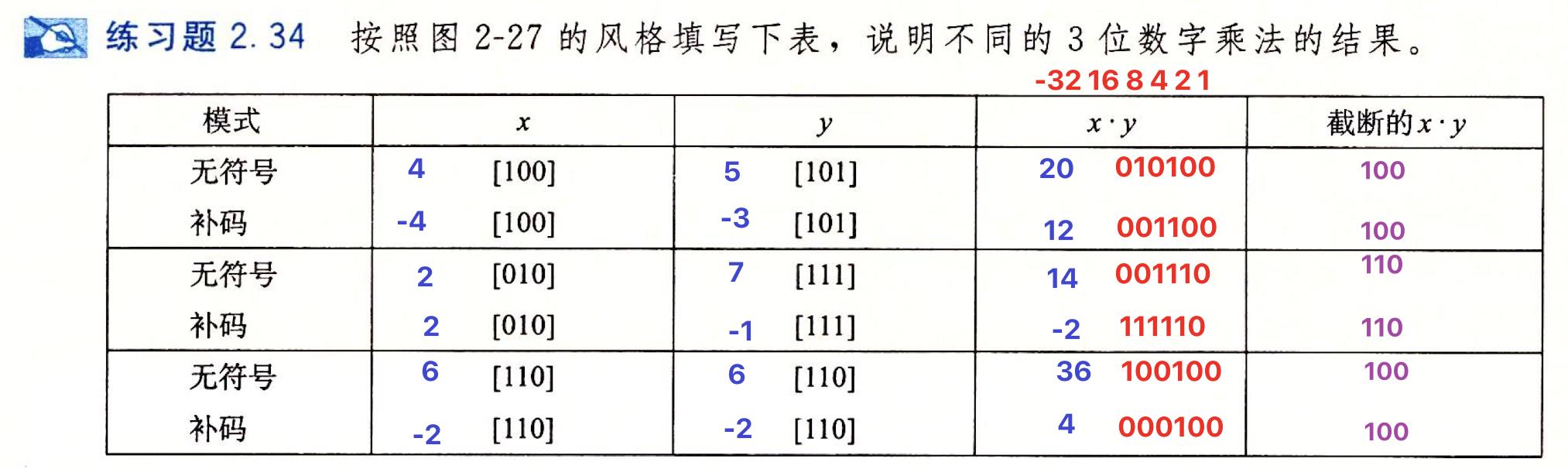
🍊优质习题
·无符号和补码乘法的位级等价性
✨✨✨我是分割线✨✨✨
🔥2.3.6·乘以常数
·以往,在大多数机器上,整数乘法指令相当慢,需要10个或者更多的时钟周期,然而其他整数运算(例如加法、减法、位级运算和移位)只需要1个时钟周期。因此,编译器试着用移位和加法运算的组合来代替乘以常数因子的乘法。
·首先考虑乘以2的幂的情况,然后再概括成乘以任意常数。
🍊1.乘以2的幂
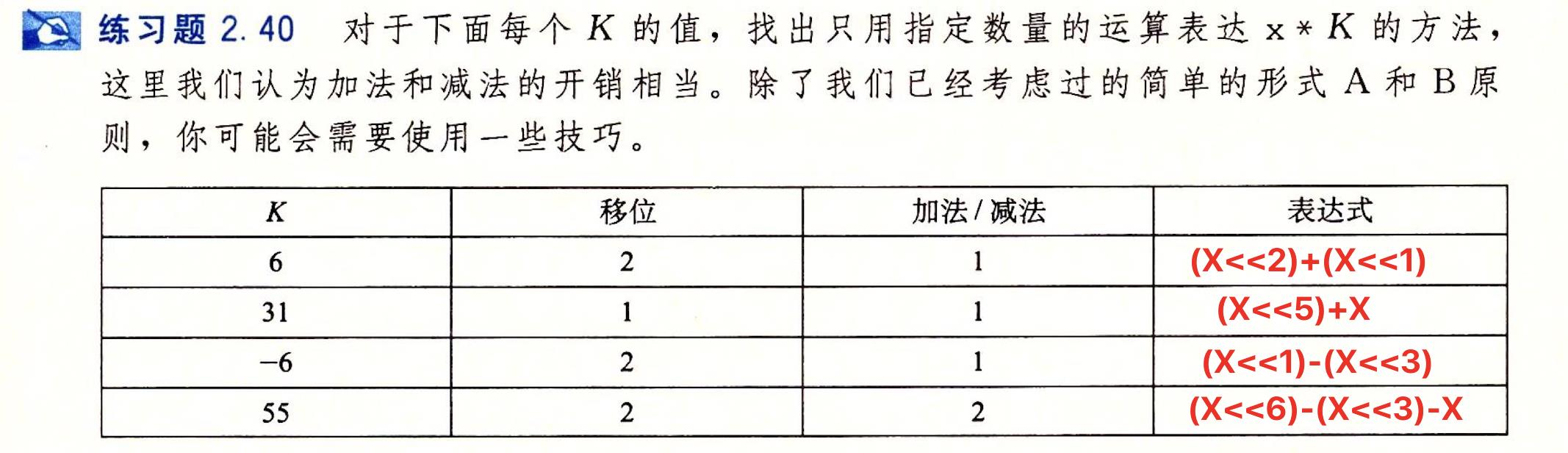
🍊2.常用解法
🍊优质例题
✨✨✨我是分割线✨✨✨
🔥2.3.7·除以2的幂
·整数除法要比整数乘法更慢——需要30个或者更多的时钟周期
·除以2的幂也可以用移位运算来实现(使用右移)
🍊1.除以2的幂的无符号除法
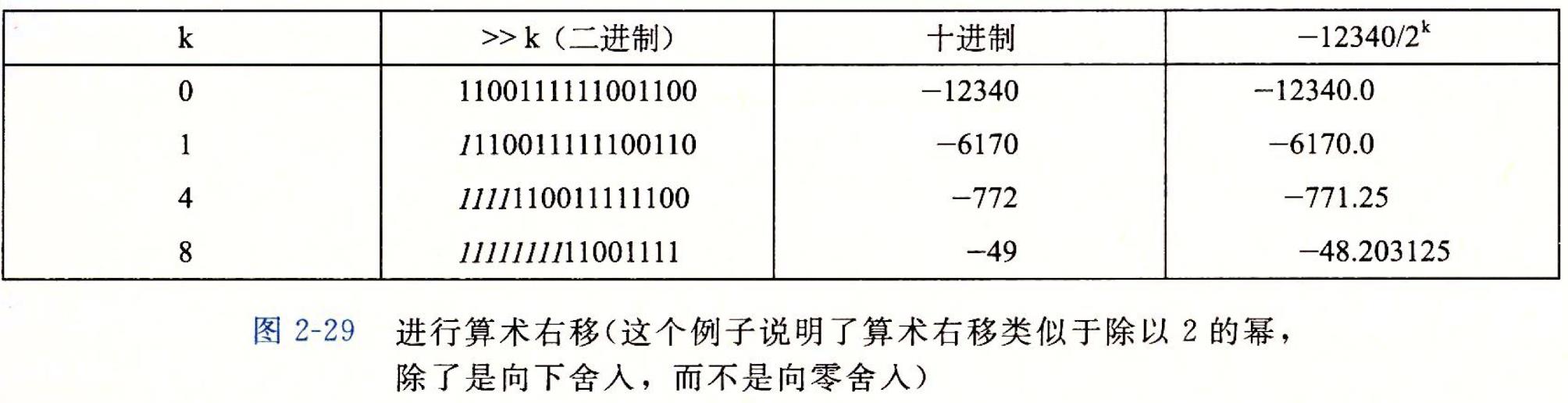
🍊2.除以2的幂的有符号除法 (向下舍入)
🍊3.除以2的幂的有符号除法(向上舍入)
✨✨✨我是分割线✨✨✨
🔥2.3.8·关于整数运算的最后思考
·计算机执行的“整数”运算实际上是一种模运算形式。表示数字的有限字长限制了可能的值的取值范围,结果运算可能溢出。我们还看到,补码表示提供了一种既能表示负数也能表示正数的灵活方法,同时使用了与执行无符号算术相同的位级实现,这些运算包括像加法、减法、乘法,甚至除法,无论运算数是以无符号形式还是以补码形式表示的,都有完全一样或者非常类似的位级行为。
🍊优质例题
✨✨✨我是分割线✨✨✨
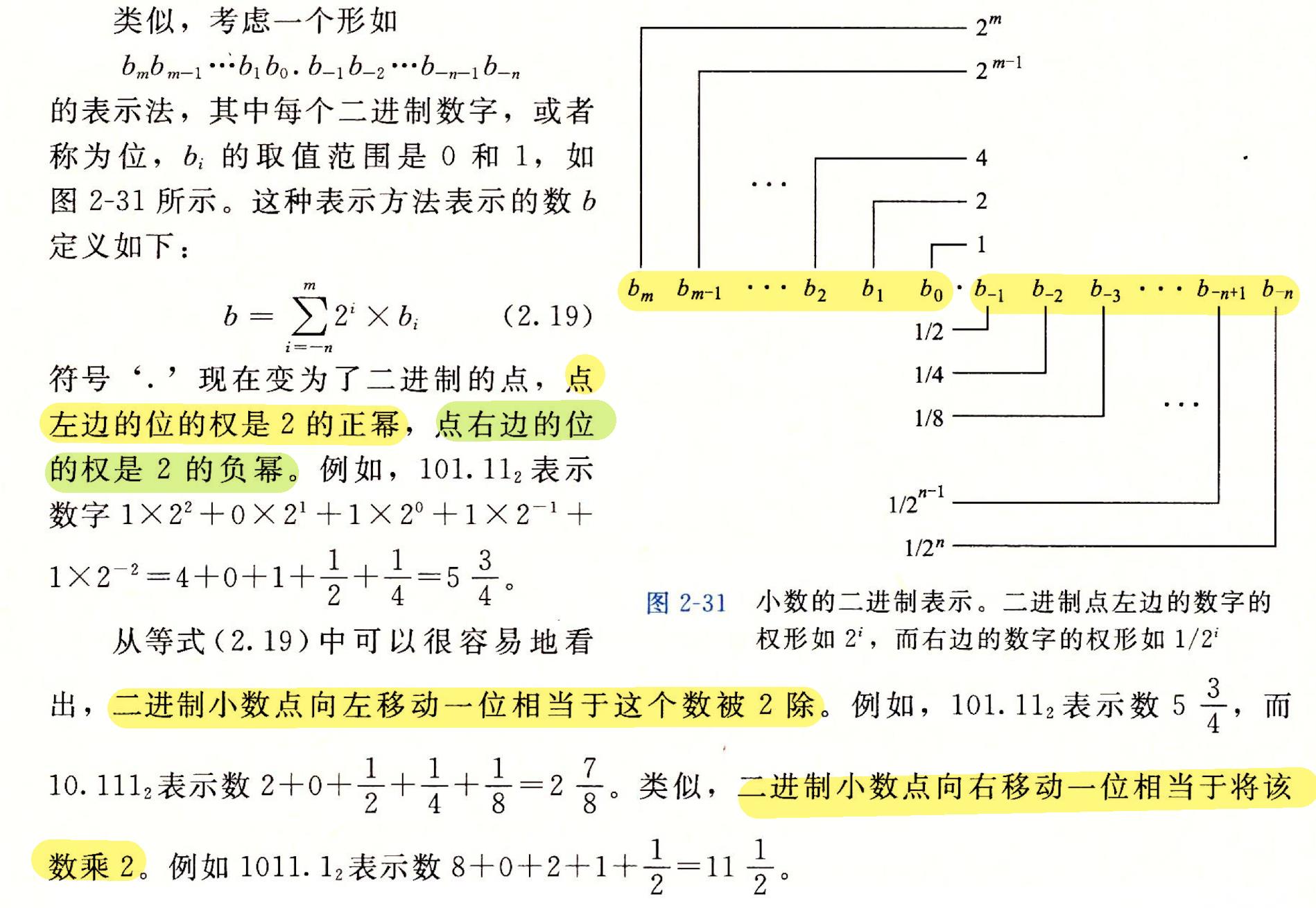
🔥2.4.1·二进制小数
🍊十进制的引子
🍊二进制小数的位权
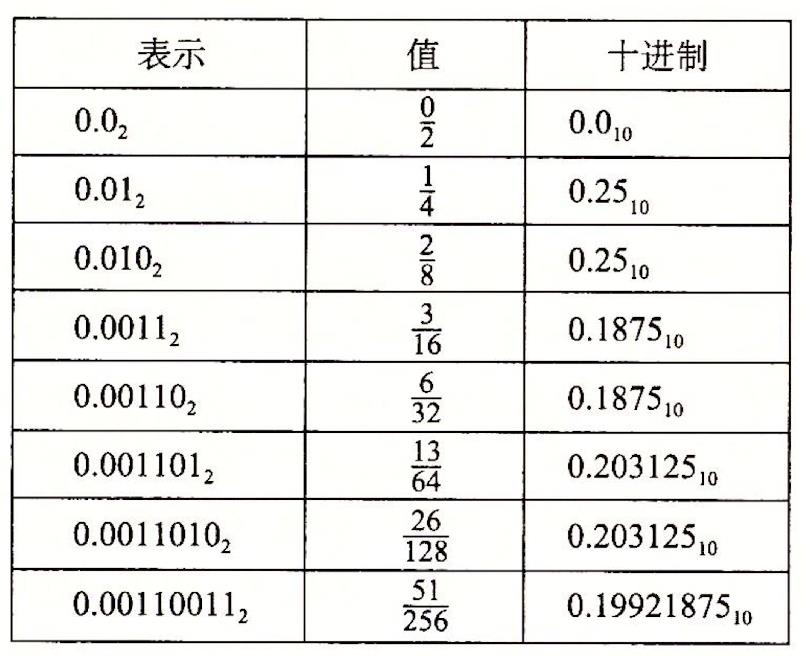
🍊二进制小数的近似表示
✨✨✨我是分割线✨✨✨
🔥2.4.2·IEEE浮点表示
·定点表示法不能有效地表示很大的数
🍊float和double的浮点表示
🍊被编码值的三种情况
🍓情况1.规格化数
🍓情况2.非规格化数
🍓情况3.特殊值
✨✨✨我是分割线✨✨✨
🔥2.4.3·数字示例
🍊典型案例
🍊典型习题
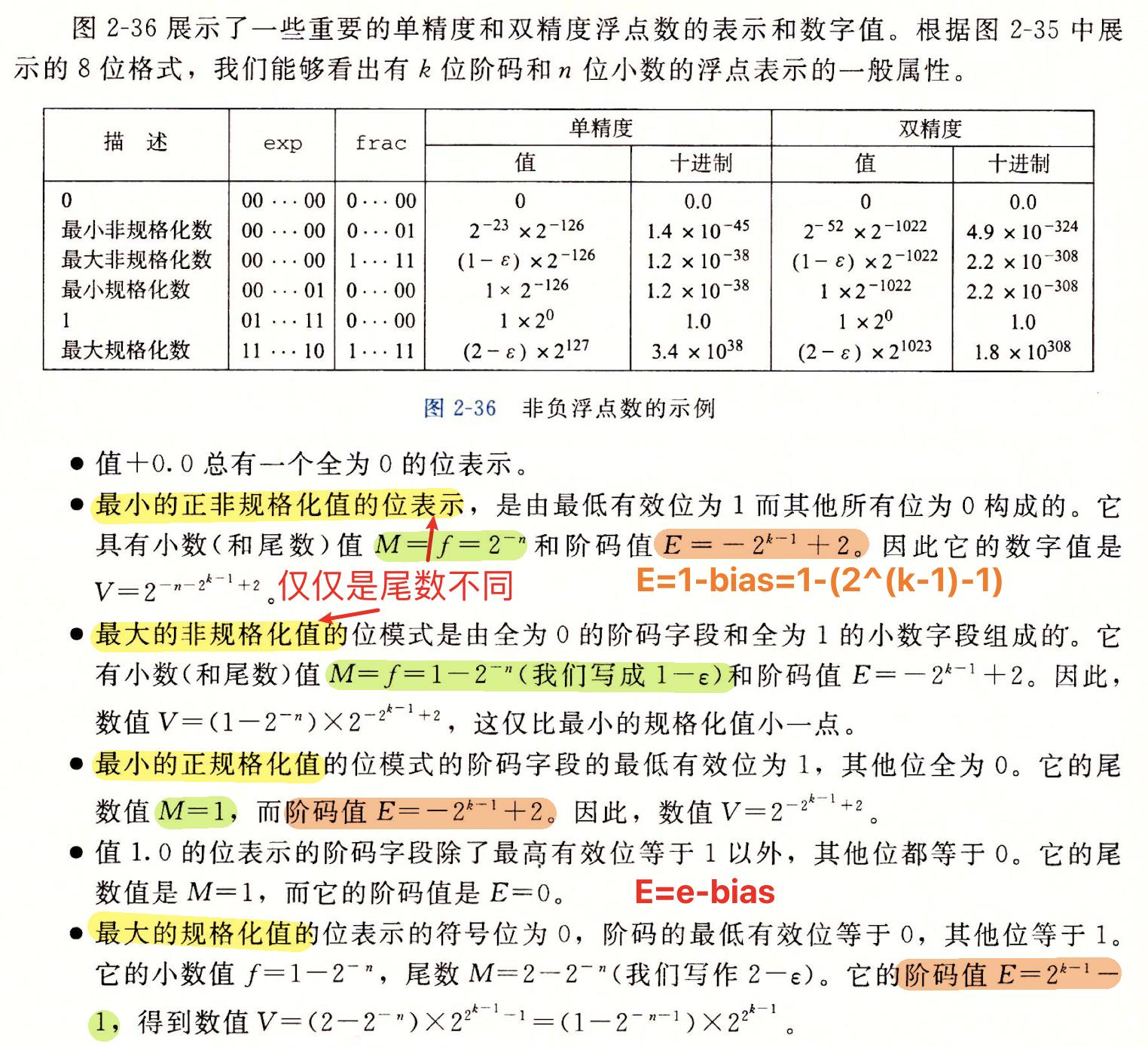
🍊最值表示
🍊整数和浮点数之间的转换
🍓练习1
✨✨✨我是分割线✨✨✨
🔥2.4.5·浮点运算
- 具有交换性
- 具有单调性
- 不具有结合性
- 不具有分配性
✨✨✨我是分割线✨✨✨
🔥2.4.6·C语言中的浮点数
🍊强制转换时的细节原则
🍊典型例题
✨✨✨我是分割线✨✨✨
🔥2.5·总结
以上是关于《深入理解计算机系统》·深度挖掘第2章·第二话的主要内容,如果未能解决你的问题,请参考以下文章