图像处理系列——直方图之直方图均衡化(Histogram Equalization)

Posted 2021-12-16 nanke_yh

目录

1、理论知识

2、数学原理

3、案例分析

4、代码实现

5、结果显示

6、参考

---

1、理论知识

        直方图均衡化是一种借助直方图变换实现灰度映射从而达到图像增强目的的方法。

        基本思想：把原始图的直方图变换成为均匀分布的形式，即对图像中像素个数多的灰度级进行展宽，而对像素个数少的灰度级进行缩减。增加了像素灰度值的动态范围，从而达到增强图像整体对比度的效果。

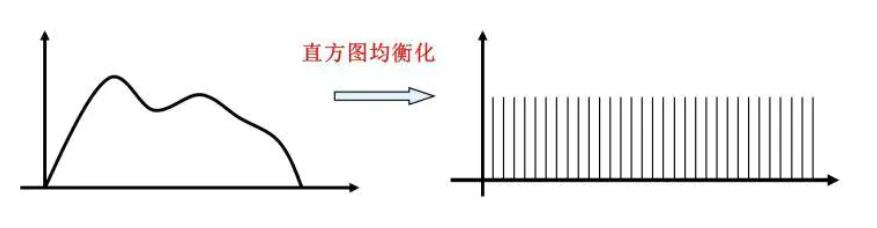
        直方图反映了图像的清晰程度，当直方图均匀分布时，图像最清晰。由此，利用直方图均衡化可以达到了使图像清晰的目的。

2、数学原理

        图像直方图均衡化采用累积分布函数：

        需要理解：1、为什么要选用累积分布函数？2、使用累积分布函数处理后像素值为什么会均匀分布？

1. 均衡化过程中，必须保证两个条件：①像素无论怎么映射，一定要保证原来的大小关系不变，较亮的区域依旧较亮，较暗依旧较暗，只是对比度增大，绝对不能明暗颠倒；②如果是八位图像，那么像素映射函数的值域应在0~255之间，不能越界。因此，累积分布函数是个好的选择，因为累积分布函数是单调增函数（控制大小关系），并且值域是0到1（控制越界问题），所以直方图均衡化中使用的是累积分布函数。
2. 累积分布函数具有一些好的性质，那么如何运用累积分布函数使得直方图均衡化？比较概率分布函数和累积分布函数，前者的二维图象是参差不齐的，后者是单调递增的。

        由于各个灰度级是离散的，上式又可以写作：

        其中，n是图像中像素的总和（n=W*H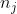），是当前灰度级的像素个数，L是图像中灰度级总数。

3、案例分析

        接图像处理系列——直方图之灰度直方图(Image Histogram)_nanke_yh的博客-CSDN博客中计算案例有：

灰度级 r	0	1	2	3	4	5	6	7
像素数量nr	792	1026	851	662	323	240	120	82
概率分布P(r)	0.19	0.25	0.21	0.16	0.08	0.06	0.03	0.02
累积分布sk	0.19	0.44	0.65	0.81	0.89	0.95	0.98	1
均衡化取值S(k)	1	3	5	6	6	7	7	7
确定映射关系r->S(k)	0->1	1->3	2->5	3,4->6		5,6,7->7
均衡化后图像直方图		0.19		0.25		0.21	0.24	0.11

        

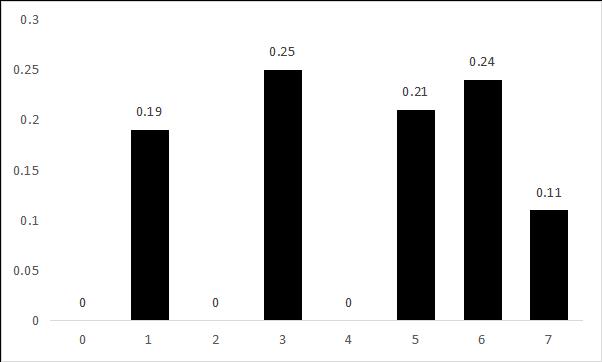
         继计算图像直方图后，图像均衡化的步骤：

（1）计算直方图概率累积分布sk

        这里s0=P0；

              s1=P0+P1；

              sk=P0+P1+……+Pk    where（k>1）。

(2)根据公式求取像素映射关系S(k)

        S(k)=int[max(pix)-min(pix)]*s(k)+0.5

        其中，pix指原图像中的灰度值，求取原图像中的最大灰度值减去最小灰度值。S(k)是第k灰度级所对应的均衡化图像中的灰度级。

        S(k)=int[(L-1)-0]*s(k)+0.5

        而有的均衡化理论中使用(L-1)-0，也就是该图像灰度级中的最大值减去灰度最小值。L是图像总灰度级数。

（3）灰度映射

        上一步找到了原图像和均衡化图像灰度的对应关系，对原图进行操作，将每个像素映射成新的像素即可。

（4）图像均衡化后图像直方图

        此时图像均衡化已经完成，可以再次统计新图像的灰度概率，观察一下结果。

4、代码实现

/*function description:图像直方图均衡化
*
*input parameter:
*				ImgTyp* Image    原始图像
*return:
*				ImgTyp* ImgEqual 直方图均衡化后的图像
******************************************************/
ImgTyp* HistogramFun::HistEqual2(ImgTyp* Image)

	if (Image == NULL)
	
		return NULL;
	
    double* ImgHist = CalImgHist(Image);//计算图像直方图概率分布
	ImgTyp*ImgEqual = new ImgTyp[Width*Height];
	memset(ImgEqual,0,sizeof(ImgTyp)*Width*Height);
	//累积分布sk
	double sk[ColorLen] = 0;
	//sk[0] = ImgHist[0];
	//for (int k = 1; k < ColorLen; k++)
	//
	//	sk[k] = sk[k-1] + ImgHist[k];//累计密度函数值
	//
	double  sum = 0;
	for (int k = 0; k < ColorLen; k++)
	
		sum += ImgHist[k];
		sk[k] = sum;//累计密度函数值
	
	for (int i = 0; i < Height; i++)
	
		for (int j = 0; j < Width; j++)
		
			int target_value = 0;
			target_value = int((ColorLen-1) * sk[Image[i*Width+j]]+0.5);//[（L-1）*s+0.5]
			if (target_value > ColorLen-1)
			
				target_value = ColorLen-1;
			
			ImgEqual[i*Width+j] = target_value;
		
	
	delete []ImgHist;
	ImgHist = NULL;
	return ImgEqual;

5、结果显示

        基于上面得出的结果进行显示：

均衡化后的图像1	target_value = int((ColorLen-1) * sk[Image[i*Width+j]]+0.5);//[（L-1-0）*s+0.5] 灰度级中的最大值减去灰度最小值 ImgTyp* imgEqual = hist.HistEqual2(img); WriteTif( imgEqual,outfile[0],hist.Width,hist.Height); showImg(outfile[0],"直方图均衡化图像1");
均衡化后图像的直方图	double* EqualhistArr = hist.CalImgHist(imgEqual); showHist(EqualhistArr,"均衡化后图像直方图1");
均衡化后的图像2	target_value = int((MMPixel[0]-MMPixel[1]) * sk[Image[i*Width+j]]+0.5);//[（max(pix)-min(pix)）*s+0.5] 图像中的最大灰度值减去最小灰度值 ImgTyp* imgEqual1 = hist.HistEqual3(img); WriteTif(imgEqual1,outfile[2],hist.Width,hist.Height); showImg(outfile[2],"直方图均衡化图像2");
均衡化后图像的直方图	double* EqualhistArr1 = hist.CalImgHist(imgEqual1); showHist(EqualhistArr1,"均衡化后图像直方图2");

        发现第二种均衡化方式得到的图像相较第一种会偏暗，直方图的色阶也会少一些。

6、参考

数字图像处理:直方图均衡化 - 简书 (jianshu.com)

直方图均衡化计算过程_macunshi的专栏-CSDN博客_直方图均衡化计算步骤

图像处理之直方图均衡化及C++实现_程序员深度学习-CSDN博客