从矩阵快速幂的泛型模板设计——教你如何优雅的面向对象
Posted C_YCBX Py_YYDS
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从矩阵快速幂的泛型模板设计——教你如何优雅的面向对象相关的知识,希望对你有一定的参考价值。
文章目录
实现源码在线查看
如果对于类的设计已经非常清楚,只是进来想看看我的这个泛型模板源代码,那么直接点到下面这个链接进行查看:
源码链接
什么是矩阵快速幂?
- 关于快速幂,就是利用二进制进行求解某个数的幂的快速方法。
后面会对快速幂的原理进行简单讲解,如果还是不懂,请自行百度。
相信有很多小伙伴是初入大学的世界,可能还没学过线性代数(比如我),于是乎不知道矩阵是什么,我推荐一个网站去看看矩阵的乘法是怎么运算的,下面是网站链接:(话说how to这个网站还真是牛批,什么东西都有教程,而且质量还贼高!😂)
那么如何用代码表示矩阵以及他的乘法呢?
其实很简单,就是三层循环进行控制即可。
如:我这里是C++的重载运算符 Matrix 是我定义的一个类。
Matrix& operator*(Matrix& b)
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++)
for(int j=0;j<b.m;j++)
ll sum = 0;
for(int k=0;k<m;k++)
sum = (sum + date[i][k]*b.date[k][j])%MOD;
tmp[i][j] = sum;
this->m = b.m;
for(int i=0;i<n;i++)
for (int j = 0; j < m; ++j)
date[i][j] = tmp[i][j];
return *this;
怎么进行矩阵快速幂的运算?
关于如何矩阵快速幂,我们先了解一下简单的快速幂。
说是快速幂就是通过位运算实现快速的同数累乘。
简述一下快速幂的原理:
原理就是,如果要求x的3次幂,那么可以转化为求 x*x 的 2 次幂,而求一个数的 2^n 幂是很简单的,比如进行一次 x *= x 便得到 x 的二次方。而再进行一次 x *= x 就得到了 4 次方,继续便可得到 8/16... 总之是 log2N 的时间。
代码如下:
int QuickPow(int x,int n)
int c = n;
int res = 1;
while(c!=0)
if(c&1!=0)
res *= x;
c >>= 1;
x *= x;
return res;
- 那么矩阵的快速幂如何进行?
把上述的 int 类型换成自己定义的矩阵就是矩阵的快速幂了。
我直接贴上C++实现的重载运算符后的类的快速幂写法:
这里的quickPow表示的是一个类的成员函数,所以可以直接用到这个矩阵里的数据进行运算。this表示指向这个对象的指针。init() 成员函数表示初始化为单位矩阵。
void quickPow(ll c)
if(c==1||c<0)return;
if(c==0)
init();
return;
Matrix tmp(*this);
init();
while (c)
if(c&1)
*this = *this * tmp;
c >>= 1;
tmp = tmp*tmp;
为什么突然想写这个模板?
主要是因为最近做了几道快速幂的题目,被坑的很惨,然后就突然想设计一个模板了,主要是 my_tiny_stl 这个仓库也好久没更新了😂
题目
我是如何被坑的
- 首先拿到这道题,我便马上开始简单的O(n)递推法实现,然后提交,然后。。超时。。
定眼一看,数据量原来这么大!
后面一想,肯定是矩阵快速幂了,先想出以下矩阵的递推式子:
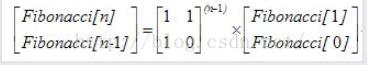
进而题目便可得到求解。
然后我就利用 C++ 的类简单的封装了一个矩阵类,里面重载了乘法和 quickpow 方法,然后比较悠闲的准备提交,还没提交前就遇到C++的语法陷阱、、
语法陷阱(建议非C++党绕道)
由于类用的都是堆内存,所以我写了析构函数,我遇到的问题出在重载乘法时我返回的是左值,而且我也没有对 ‘=’ 进行重载,所以 ‘=’ 就是直接的成员变量拷贝,这导致一个结果就是两个对象的 date 指向同一片内存空间,而之前的那片内存空间泄露了,且最后这两个对象肯定都会调用析构函数,这又导致了析构函数调用了两次!
- 如何解决这个问题?如果是
C++98,那么这个问题很大,基本上就是两种方法解决:
- 逃避问题,乘法的左操作数必须是当前赋值对象,这样就避免了最后赋值语句将原本对象内的指针直接改变。
- 解决问题,解决这类问题无论是
C++11还是C++98最直接的方式就是重载‘=’号,重载'='号的实现根据具体的情况进行,而具体实现赋值的重载,我们需要考虑两件事:第一,需尽可能的减少内存的申请和使用(具体而言就是判断两个对象的指针所指向的是否为同一片空间,即便不是同一片空间,为了增加空间利用率还可以判断两个空间是否大小一致,然后进行拷贝即可)。第二,如果是临时对象则需要把它的指针置空(防止编译器未优化临时变量的析构函数,从而调用了析构函数多次析构同一内存)。
- 由于
C++11开始有了右值引用和它配套的移动赋值构造器,所以可以把临时变量直接调用移动构造器变成具名对象,然后进行操作,一般就是把它的指针所有权进行转移,然后把它的指针置空防止析构错误,在我的理解下,右值引用的出现就是为了捕捉到匿名对象然后给程序员进行适当的性能优化操作,没有右值引用前,匿名对象的内存根本就没法去使用,只能用来简单的赋值拷贝操作后才能使用,这样就很消耗内存了,右值引用出现后,我们可以通过右值引用对匿名对象进行捕捉,然后操作它的底层内存。还有一个很大的内存相关的更新就是有了一个nullptr关键字,这个关键字使得空指针不再会有歧义,所以delete nullptr是安全的。所以防止多次delete同一片空间产生错误可以将它赋值为nullptr即可。 - 那么基于
C++11这个问题该如何解决呢?解决方法和C++98没差,就是能够更加得心应手的进行内存的管理了,如果等号右边是一个右值,那么它肯定是一个临时对象,所以我们可以在 ‘=’ 号的重载中直接了当的用它的内存,并把它的指针置空。如果没有右值类型进行捕获,编译器默认也是会对临时对象进行优化的,也能防止产生多个对象的赋值拷贝,但只能在对象初始化的时候进行优化!而在其他时候则还是会调用析构函数,这个时候如果还是用编译器默认产生的 ‘=’ 重载,则会发生被析构的空间的指针被赋值的情况,而我们的右值引用版本的赋值重载便是针对此现象的。这样便于内存管理,将右值和左值进行分开处理。右值是临时变量只需要用一会儿,所以可以直接把它的内存拿过来继续用,也不会对程序逻辑造成影响,而左值则不一样,它还需要存活很长一段时间,所以我们需要另创空间进行拷贝。
特别提醒:如果是做算法题,则完全不用去考虑内存的管理,析构函数也不要去写,毕竟只需要单次调用使用,对象最多也就存在一会儿。
做题陷阱
在必要的时候千万不要舍不得开long long!!!!
这道题的数据量无论是幂的次方还是整个记录过程的数据都要开long long!!!
我被这个陷阱坑了无数回了,这一次也不另外😅
开始写完这种之后过了前5个,然后后面5个报错,我还以为我设计的这个类有问题,还特意去写了好几个普通C语言版本😂最后发现原来的没开long long。以下为更改long long后的代码通过版本,我用宏定义写了几个版本。。。
这个Matrix类的设计还是很多地方没有考虑到位,比如上一个陷阱的问题只是通过方法一得到解决,并未去重载赋值操作符。。。所以后面痛定思痛,设计一个较为可用的Matrix类!
- 效率时快时慢的,这主要取决于编译器是否进行优化。

//
// Created by Alone on 2021/11/19.
//
#include <bits/stdc++.h>
using namespace std;
//#define ELSE_MAIN
#define MY_MAIN
#define MAT
#ifdef MAT
typedef long long ll;
class Matrix
ll** date;
int m;
int n;
public: static const int MOD;
public:
Matrix(ll** rec,int n,int m):date(rec),n(n),m(m)//C风格的初始化
Matrix():date(NULL),m(0),n(0) //缺省
Matrix(Matrix& b):n(b.n),m(b.m)//拷贝构造
assert(b.date!=NULL && b.n>0 && b.m>0);
date = new ll*[n];
copy(b.date,b.date+n,date);
for(int i=0;i<n;i++)
date[i] = new ll[m];
copy(b.date[i],b.date[i]+m,date[i]);
~Matrix()//析构函数实现
assert(date!=NULL && n>0 && m>0);
for (int i = n-1; i >=0 ; --i)
delete [] date[i];
delete[] date;
Matrix& operator*(Matrix& b)
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++)
for(int j=0;j<b.m;j++)
ll sum = 0;
for(int k=0;k<m;k++)
sum = (sum + date[i][k]*b.date[k][j])%MOD;
tmp[i][j] = sum;
this->m = b.m;
for(int i=0;i<n;i++)
for (int j = 0; j < m; ++j)
date[i][j] = tmp[i][j];
return *this;
void init()//重新初始化为单位矩阵
assert(date!=NULL && n>0 && m>0);
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
if(i==j)date[i][j] = 1;
else date[i][j] = 0;
void quickPow(ll c)
if(c==1||c<0)return;
if(c==0)
init();
return;
Matrix tmp(*this);
init();
while (c)
if(c&1)
*this = *this * tmp;
c >>= 1;
tmp = tmp*tmp;
void print()
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cout<<date[i][j]<<' ';
cout<<endl;
int get(int x,int y)
assert(date!=NULL && x<n && y<m);
return date[x][y];
;
const int Matrix::MOD = 1e9+7;
#endif
#ifdef MY_MAIN
int main()
ll c;
cin>>c;
ll** matrix = new ll*[2];
matrix[0] = new ll[2]1,1;
matrix[1] = new ll[2]1,0;
Matrix mat(matrix,2,2);
mat.quickPow(c-1);
//mat.print();
ll** res = new ll*[2];
res[0] = new ll[1];
res[1] = new ll[1];
res[0][0] = res[1][0] = 1;
Matrix fib(res,2,1);
//这里有个内存分配错误,mat*fib返回的是左值,而=没有重载默认直接赋值成员变量。
//直接导致了fib失去了之前的变量所有权,和mat共同有一个内存空间,这样导致同一片空间被free两次
//通过重载 = 号解决,防止直接的内存没有被释放就重新绑定同一片内存
Matrix ret(mat*fib);
cout<<ret.get(0,0);
return 0;
#endif
#ifdef TEST_MAIN
typedef long long ll ;
const int MOD = 1e9+7;
ll a[2][2]1,1,1,0;ll b[2]1,1;
void selfMut()
ll tmp[2][2];
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
ll sum = 0;
for(int k=0;k<2;k++)
sum = (sum+a[i][k]*a[k][j])%MOD;
tmp[i][j] = sum;
for(int i=0;i<2;i++)
memmove(a[i],tmp[i],sizeof(tmp[i]));
void difMut()
ll tmp[2];
for(int i=0;i<2;i++)
ll sum = 0;
for(int k=0;k<2;k++)
sum = (sum + a[i][k]*b[k])%MOD;
tmp[i] = sum;
b[0] = tmp[0];
b[1] = tmp[1];
void Mut(ll _a[2][2],ll _b[2][2],int n1,int m1,int n2,int m2)
if(m1!=n2)
return ;
int tmp[n1][m2];
for(int i=0;i<n1;i++)
for(int j=0;j<m2;j++)
ll sum = 0;
for(int k=0;k<m1;k++)
sum = (sum+_a[i][k]*_b[k][j])%MOD;
tmp[i][j] = sum;
for(int i=0;i<n1;i++)
for(以上是关于从矩阵快速幂的泛型模板设计——教你如何优雅的面向对象的主要内容,如果未能解决你的问题,请参考以下文章