一种用几何解nonlinear ICA的方法

Posted 2021-12-15 Jie Qiao

注：本文是gpICA: A Novel Nonlinear ICA Algorithm Using Geometric Linearization的论文笔记

线性ICA

考虑n个可观测的变量$\mathbf{x}=[x_1,...,x_n{]}^T$，以及不可观察但相互独立的n个源噪声$\mathbf{s}=[s_1,...,s_n{]}^T$，其中x是经过一个mixing matrix$\mathbf{A}\in {\mathbb{R}}^{n\times n}$产生的：

$$\mathbf{x}=\mathbf{A}\mathbf{s}$$

ICA的任务就是从可观测的n个x中恢复出真实的A和s. 这个问题在s是非高斯的情况下是可恢复的，不再赘述。

Noinlinear ICA

类似的，考虑生成方式

$$\mathbf{x}=f(\mathbf{s})$$

这里f是一个非线性函数，那么能否从x恢复出s呢。这问题已被证明在没有额外假设下是不可行的，必须要增加一些额外的假设，一个典型的是Post nonlinear model (PNL):

$$x_i=f_i(\mathbf{A}\mathbf{s}),i=1,...,n$$

PNL的几何解法

PNL模型是已被证明是可识别的，但这里给出一种非常有趣的几何法来求解他，过程如下示意图所示：

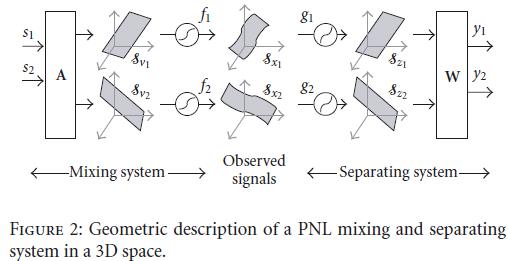
以2维作为例子，可以分别将$(s_1,s_2,x_1)$和$(s_1,s_2,x_2)$作为坐标画出两个经过线性变换得到的平面，然后分别加上一个非线性变换$f_i$得到两个曲面。我们知道如果是平面那么就退化到linear ICA的情况是可解的，所以PNL的任务就是想办法讲曲面变成平面。

然而一个问题是，我们实际只能观测到z轴上的值，s1，s2是观测不到的，也就是$(\_,\_,z)$. 这里提供一种几何的方法来完成这件事情，这里先定义companion pair

我们称$p_1(x,y,z_1),p_2(x,y,z_2)$，这种只有z轴不同的点称为companion pair. 可以证明，对于任意的点，$(\_,\_,z_{p_1})$和对应的companion$(\_,\_,z_{q_1})$，以及$(\_,\_,z_{p_2})$和对应的compansion$(\_,\_,z_{q_2})$. 我们进一步取，直线$p_1{p}_2$之间任意的一个点$(\_,\_,z_c)$，还有其对应的在直线$q_1{q}_2$上的compansion$(\_,\_,z_{q_c})$，那么一定有以下关系成立

$$\frac{z_{pc}-z_{p1}}{z_{p2}-z_{p1}}=\frac{z_{qc}-z_{q1}}{z_{q2}-z_{q1}}$$

这意味着， 给定5个点$p_1,p_2,q_1,q_2,p_c$能够预测出第六个点的位置$p_{q_c}.$

这个理论有什么用？以下图为例子：

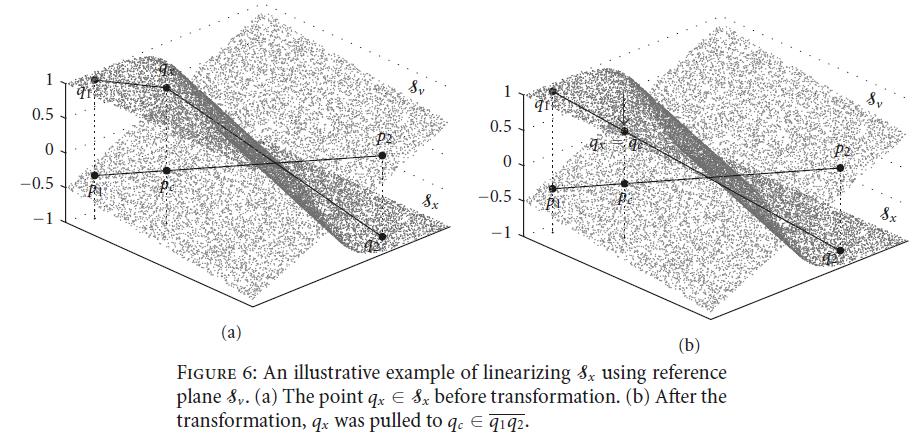
给定一个曲面和一个任意平面，这个曲面是其中一个$x_1$的曲面，显然我们可以在平面上随意选两个点$p_1,p_2$还有两条线之间的$p_c$。接下来，在曲面上也选择对应的companion， q 1 , q 2 , q c

以上是关于一种用几何解nonlinear ICA的方法的主要内容，如果未能解决你的问题，请参考以下文章

内容

独立成分分析 ICA 原理及公式推导 示例

ICA （独立成分分析）

css 一种用css-modules写嵌套css的技巧方法

线性回归有解析解为啥还要用梯度下降

插值相关总结