BP（Back Propagation）神经网络——应用篇

Posted 2021-12-15 AXYZdong

Author：AXYZdong 自动化专业 工科男
有一点思考，有一点想法，有一点理性！
定个小小目标，努力成为习惯！在最美的年华遇见更好的自己！
CSDN@AXYZdong，CSDN首发，AXYZdong原创
唯一博客更新的地址为： 👉 AXYZdong的博客 👈
B站主页为：AXYZdong的个人主页

文章目录

• 1. 9行代码的BP神经网络
• • short_version.py
• 2. main.py
• • 源代码（适用python2环境）
  • 稍加修改（适用python3环境）
• 3. 总结
• 参考文献

关于BP神经网络的原理可以参考我的上一篇文章：BP（Back Propagation）神经网络——原理篇

1. 9行代码的BP神经网络

代码来源于github：https://github.com/miloharper/simple-neural-network

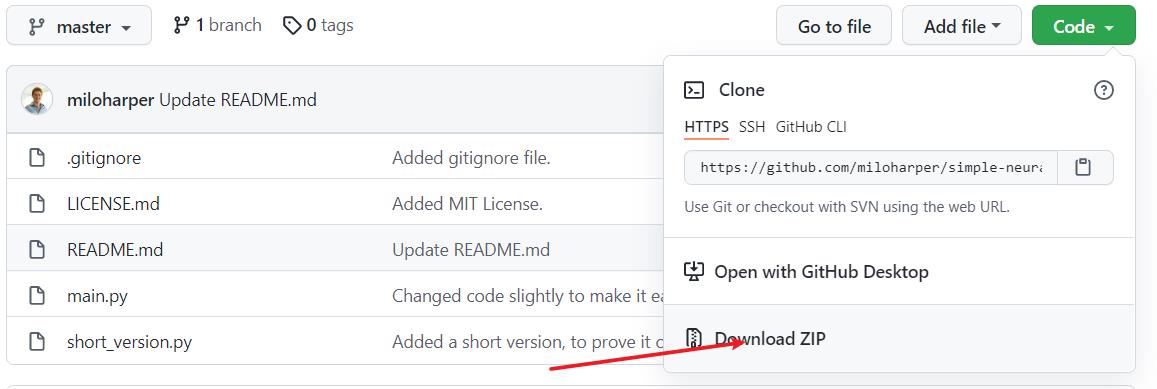
下载解压后得到如下文件：

short_version.py

from numpy import exp, array, random, dot 
#从numpy库中调用exp(指数函数）、array(数组〉、random（随机函数)、dot(矩阵相乘函数)。
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
#bp神经网络训练部分的输入。
training_set_outputs = array([[0, 1, 1, 0]]).T
#bp神经网络训练部分的输出，.T表示矩阵转置。
random.seed(1)
#使用随机函数生成随机数，使用seed函数能够确保每次生成的随机数一致。
synaptic_weights = 2 * random.random((3, 1)) - 1
#生成一个随机数组，数组格式为3行1列，用来存储初始权重。
for iteration in range(10000):
    output = 1 / (1 + exp(-(dot(training_set_inputs, synaptic_weights))))
    #使用for语句循环10000次，将训练集的输入和权重采用dot进行矩阵相乘，将相乘得到的结果输入到sigmoid函数,然后将得到的结果赋值给output。
    synaptic_weights += dot(training_set_inputs.T, (training_set_outputs - output) * output * (1 - output))
    #权重的i调整采用“误差加权导数""公式。
print (1 / (1 + exp(-(dot(array([1, 0, 0]), synaptic_weights)))))
#synaptic_weights是调整之后的最终权重，数组（矩阵〉[1,0，0]与这个权重矩阵通过dot函数进行相乘，将相乘的结果作为输入引入到sigmoid函数，得到最终的结果。

运行结果：

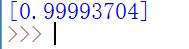
2. main.py

源代码（适用python2环境）

from numpy import exp, array, random, dot


class NeuralNetwork():
    def __init__(self):
        # Seed the random number generator, so it generates the same numbers
        # every time the program runs.
        random.seed(1)

        # We model a single neuron, with 3 input connections and 1 output connection.
        # We assign random weights to a 3 x 1 matrix, with values in the range -1 to 1
        # and mean 0.
        self.synaptic_weights = 2 * random.random((3, 1)) - 1

    # The Sigmoid function, which describes an S shaped curve.
    # We pass the weighted sum of the inputs through this function to
    # normalise them between 0 and 1.
    def __sigmoid(self, x):
        return 1 / (1 + exp(-x))

    # The derivative of the Sigmoid function.
    # This is the gradient of the Sigmoid curve.
    # It indicates how confident we are about the existing weight.
    def __sigmoid_derivative(self, x):
        return x * (1 - x)

    # We train the neural network through a process of trial and error.
    # Adjusting the synaptic weights each time.
    def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
        for iteration in xrange(number_of_training_iterations):
            # Pass the training set through our neural network (a single neuron).
            output = self.think(training_set_inputs)

            # Calculate the error (The difference between the desired output
            # and the predicted output).
            error = training_set_outputs - output

            # Multiply the error by the input and again by the gradient of the Sigmoid curve.
            # This means less confident weights are adjusted more.
            # This means inputs, which are zero, do not cause changes to the weights.
            adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))

            # Adjust the weights.
            self.synaptic_weights += adjustment

    # The neural network thinks.
    def think(self, inputs):
        # Pass inputs through our neural network (our single neuron).
        return self.__sigmoid(dot(inputs, self.synaptic_weights))


if __name__ == "__main__":

    #Intialise a single neuron neural network.
    neural_network = NeuralNetwork()

    print "Random starting synaptic weights: "
    print neural_network.synaptic_weights

    # The training set. We have 4 examples, each consisting of 3 input values
    # and 1 output value.
    training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
    training_set_outputs = array([[0, 1, 1, 0]]).T

    # Train the neural network using a training set.
    # Do it 10,000 times and make small adjustments each time.
    neural_network.train(training_set_inputs, training_set_outputs, 10000)

    print "New synaptic weights after training: "
    print neural_network.synaptic_weights

    # Test the neural network with a new situation.
    print "Considering new situation [1, 0, 0] -> ?: "
    print neural_network.think(array([1, 0, 0]))

稍加修改（适用python3环境）

from numpy import exp, array, random, dot


class NeuralNetwork():
    def __init__(self):
        # Seed the random number generator, so it generates the same numbers
        # every time the program runs.
        random.seed(1)

        # We model a single neuron, with 3 input connections and 1 output connection.
        # We assign random weights to a 3 x 1 matrix, with values in the range -1 to 1
        # and mean 0.
        self.synaptic_weights = 2 * random.random((3, 1)) - 1

    # The Sigmoid function, which describes an S shaped curve.
    # We pass the weighted sum of the inputs through this function to
    # normalise them between 0 and 1.
    def __sigmoid(self, x):
        return 1 / (1 + exp(-x))

    # The derivative of the Sigmoid function.
    # This is the gradient of the Sigmoid curve.
    # It indicates how confident we are about the existing weight.
    def __sigmoid_derivative(self, x):
        return x * (1 - x)

    # We train the neural network through a process of trial and error.
    # Adjusting the synaptic weights each time.
    def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
        for iteration in range(number_of_training_iterations):
            # Pass the training set through our neural network (a single neuron).
            output = self.think(training_set_inputs)

            # Calculate the error (The difference between the desired output
            # and the predicted output).
            error = training_set_outputs - output

            # Multiply the error by the input and again by the gradient of the Sigmoid curve.
            # This means less confident weights are adjusted more.
            # This means inputs, which are zero, do not cause changes to the weights.
            adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))

            # Adjust the weights.
            self.synaptic_weights += adjustment

    # The neural network thinks.
    def think(self, inputs):
        # Pass inputs through our neural network (our single neuron).
        return self.__sigmoid(dot(inputs, self.synaptic_weights))


if __name__ == "__main__":

    #Intialise a single neuron neural network.
    neural_network = NeuralNetwork()

    print ("Random starting synaptic weights: ")
    print (neural_network.synaptic_weights)

    # The training set. We have 4 examples, each consisting of 3 input values
    # and 1 output value.
    training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
    training_set_outputs = array([[0, 1, 1, 0]]).T

    # Train the neural network using a training set.
    # Do it 10,000 times and make small adjustments each time.
    neural_network.train(training_set_inputs, training_set_outputs, 10000)

    print ("New synaptic weights after training: ")
    print (neural_network.synaptic_weights)

    # Test the neural network with a new situation.
    print ("Considering new situation [1, 0, 0] -> ?: ")
    print (neural_network.think(array([1, 0, 0])))

运行结果：

待续…

3. 总结

• 9行代码实现BP神经网络是一种单神经网络（simple-neural-network），简洁的代码反映了BP神经网络的基本原理；
• 对比两种实现方式，9行代码很简洁，却只适合特殊的情形下。而在 main,py 中更多的是将各个函数封装模块化，便于移植。且清晰的注释增强了代码的可读性。

参考文献

[1] BP（Back Propagation）神经网络——原理篇
[2] https://github.com/miloharper/simple-neural-network

  本次的分享就到这里

---

如果我的博客对你有帮助、如果你喜欢我的博客内容，请 “点赞” “收藏” “关注” 一键三连哦！
更多精彩内容请前往 AXYZdong的博客

---

如果以上内容有任何错误或者不准确的地方，欢迎在下面 👇 留个言。或者你有更好的想法，欢迎一起交流学习~~~