LeetCode 二叉树专项验证二叉搜索树（98）

Posted 2021-12-15 TakingCoding4Granted

文章目录

• • 1. 题目
  • • 1.1 示例
    • 1.2 说明
    • 1.3 限制
  • 2. 解法一（递归中序遍历）
  • • 2.1 分析
    • 2.2 实现
    • 2.3 复杂度
  • 3. 解法二（迭代中序遍历）
  • • 3.1 分析
    • 3.2 解答
    • 3.3 复杂度
  • 4. 解法三（基于定义的递归解法）
  • • 4.1 分析
    • 4.2 解答
    • 4.3 复杂度

1. 题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数；
• 节点的右子树只包含 大于 当前节点的数；
• 所有左子树和右子树自身必须也是二叉搜索树。

1.1 示例

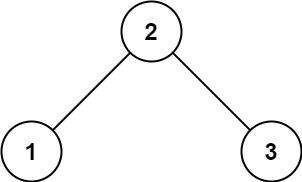
• 示例 $1$ ：

• 输入： root = [2, 1, 3]
• 输出： true

• 示例 $2$ ：

• 输入： root = [5, 1, 4, null, null, 3, 6]
• 输出： false
• 解释： 根节点的值是 $5$ ，但是右子节点的值是 $4$ 。

1.2 说明

• 来源： 力扣（LeetCode）
• 链接： https://leetcode-cn.com/problems/validate-binary-search-tree

1.3 限制

• 树中节点数目范围在 $[1,10^4]$ 内；
• $-2^{31}<=\text{Node.val}<=2^{31}-1$ 。

2. 解法一（递归中序遍历）

2.1 分析

由于这是一棵二叉搜索树，所以其中序遍历必定得到一个单调递增序列，因此只需要对给定二叉树进行中序遍历，遍历的同时判断相邻节点的 val 值是否满足单调递增的关系，如果不是则立马返回，同时在遍历过程中维护一个实例属性 self._validity 用以标示给定的二叉树是否是二叉搜索树，在中序遍历返回后将该实例属性作为结果进行返回。

2.2 实现

from typing import Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def __init__(self):
        self._prev = float('-inf')
        self._cur = float('-inf')
        self._validity = True

    def _is_valid_bst(self, root: TreeNode):
        if not root:
            return
        self._is_valid_bst(root.left)
        self._cur = root.val
        if self._cur <= self._prev:
            self._validity = False
            return
        self._prev = root.val
        self._is_valid_bst(root.right)

    def is_valid_bst(self, root: TreeNode) -> Optional[bool]:
        self._is_valid_bst(root)
        return self._validity


def main():
    node5 = TreeNode(6)
    node4 = TreeNode(3)
    node3 = TreeNode(4, left=node4, right=node5)
    node2 = TreeNode(1)
    node1 = TreeNode(5, left=node2, right=node3)
    root = node1
    sln = Solution()
    print(sln.is_valid_bst(root))  # False


if __name__ == '__main__':
    main()

2.3 复杂度

• 时间复杂度： $O(n)$，其中 $n$ 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 $O(n)$ 。
• 空间复杂度： $O(n)$，其中 $n$ 为二叉树的节点个数。因为递增调用隐式使用的栈最多会有 $n$ 层，因此需要额外的 $O(n)$ 的空间。

3. 解法二（迭代中序遍历）

3.1 分析

二叉树的中序遍历除了递归形式，还有迭代形式的二叉树中序遍历，基于后者可以给出如下的解答：

3.2 解答

from typing import Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def is_valid_bst(self, root: TreeNode) -> Optional[bool]:
        if not isinstance(root, TreeNode):
            return
        cursor = root
        stack = []
        prev = float('-inf')
        while True:
            if cursor:
                stack.append(cursor)
                cursor = cursor.left
            elif stack:
                node = stack.pop()
                cur = node.val
                if cur <= prev:
                    return False
                prev = node.val
                cursor = node.right
            else:
                break
        return True


def main():
    node5 = TreeNode(6)
    node4 = TreeNode(3)
    node3 = TreeNode(4, left=node4, right=node5)
    node2 = TreeNode(1)
    node1 = TreeNode(5, left=node2, right=node3)
    root = node1
    sln = Solution()
    print(sln.is_valid_bst(root))  # False


if __name__ == '__main__':
    main()

3.3 复杂度

• 时间复杂度： $O(n)$，其中 $n$ 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 $O(n)$ 。
• 空间复杂度： $O(n)$，其中 $n$ 为二叉树的节点个数。因为迭代使用的栈 stack 最多会有 $n$ 个元素（此时给定的二叉树呈链状），因此需要额外的 $O(n)$ 的空间。

4. 解法三（基于定义的递归解法）

4.1 分析

实际上，上述两种解答的分析都不是十分严谨，因为这里仅仅使用了一棵二叉树是一棵二叉搜索树的一个必要条件，即其中序遍历得到的序列一定是单调递增的；但是并没有进一步证明一棵二叉树是二叉搜索树的一个充分条件是该二叉树的中序遍历序列是单调递增的。之所以没有给出严谨的分析，是因为暂时我也不知道（待填坑 :) ），如果有哪位碰巧看到这篇题解的朋友知道可以在留言区一起探讨。

• 作者： LeetCode-Solution

因此，最严谨的解法是基于二叉搜索树的定义，即：

• 如果给定二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；
• 如果给定二叉树的右子树不为空，则右子树上所有节点的值均大于它的根节点的值；
• 给定二叉树的左右子树也为二叉搜索树。

这启示我们设计一个递归函数 _check_validity(root, lower, upper) 来递归判断，函数表示考虑以 root 为根的子树，判断子树中所有节点的值是否都在 (lower, upper) 的范围内（注意是开区间）。如果 root 节点的值 val 不在 (lower, upper) 的范围内说明不满足条件直接返回，否则我们要继续递归调用检查它的左右子树是否满足，如果都满足才说明这是一棵二叉搜索树。

根据二叉搜索树的性质，在递归调用左子树时，我们需要把上界 upper 改为 root.val，因为左子树里所有节点的值均小于它的根节点的值。同理递归调用右子树时，我们需要把下界 lower 改为 root.val ，因为右子树里所有节点的值均大于它的根节点的值。

函数递归调用的入口为 _check_validity(root, -inf, +inf) ， inf 表示一个无穷大的值。

4.2 解答

from typing import Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def __init__(self):
        self._validity = True

    def _check_validity(self, root: TreeNode, lower=float('-inf'), upper=float('inf')) -> Optional[bool]:
        if not isinstance(root, TreeNode):
            return
        self._check_validity(root.left, lower, root.val)
        if root.val >= upper or root.val <= lower:
            self._validity = False
            return
        self._check_validity(root.right, root.val, upper)

    def is_valid_bst(self, root: TreeNode) -> Optional[bool]:
        self._check_validity(root)
        return self._validity


def main():
    node5 = TreeNode(6)
    node4 = TreeNode(3)
    node3 = TreeNode(4, left=node4, right=node5)
    node2 = TreeNode(1)
    node1 = TreeNode(5, left=node2, right=node3)
    root = node1
    sln = Solution()
    print(sln.is_valid_bst(root))  # False


if __name__ == '__main__':
    main()

4.3 复杂度

• 时间复杂度： $O(n)$ ，其中 $n$ 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 $O(n)$ 。
• 空间复杂度： $O(n)$ ，其中 $n$ 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度。最坏情况下二叉树为一条链，树的高度为 $n$ ，递归最深达到 $n$ 层，故最坏情况下空间复杂度为 $O(n)$ 。