LeetCode 391. 完美矩形（扫描线） / 318. 最大单词长度乘积 / 563. 二叉树的坡度

Posted 2021-12-15 Zephyr丶J

391. 完美矩形

2021.11.16 每日一题

题目描述

给你一个数组 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ，右上顶点是 (ai, bi) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

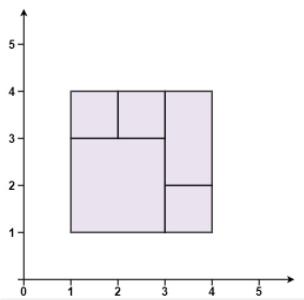
示例 1：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。

示例 2：

输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

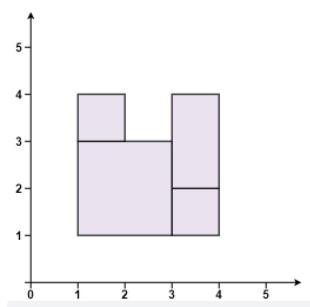
示例 3：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
输出：false
解释：图形顶端留有空缺，无法覆盖成一个矩形。

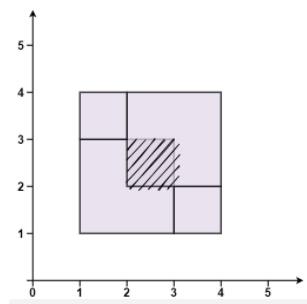
示例 4：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：false
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

提示：

1 <= rectangles.length <= 2 * 10^4
rectangles[i].length == 4
-10^5 <= xi, yi, ai, bi <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/perfect-rectangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

官解给的思路，就是按照面积和每个点出现的次数来做的

class Solution 
    public boolean isRectangleCover(int[][] rectangles) 
        //看了一下提示，扫描线，但是怎么扫描呢
        //将这个数组按照左下角排序
        //然后从左到右扫描，可以确定左边的起始位置和高度
        //然后如果补全了当前位置的高度，就向右边移动扫描线，如果不行就false

        //看了题解，感觉自己硬想扫描线去了，忘了最基础的东西
        //要想成为一个精确覆盖的矩形，那么所有矩形的面积之和，应该是和总面积相等的，这是一个大前提
        //但是光面积相等是不够的，因为比如在示例2中，如果还有一个矩形，它的下标是[1,3,4,4]
        //那么面积相加也是等于总面积的，但是并不是一个完美矩形，因为有重合部分
        //那么如果检测这部分呢，官解给出的方法是统计每个点的出现次数
        //如果是四个角的顶点，那么肯定只能出现一次
        //如果是其他顶点，那么出现两次或者四次是正常的，如果出现一次或者三次，说明肯定有没有拼接上的地方，所以false
        //那么按照这个思路写一下
        Map<Point, Integer> map = new HashMap<>();
        long area = 0;      //面积
        int leftdownX = Integer.MAX_VALUE;
        int leftdownY = Integer.MAX_VALUE;
        int rightupX = Integer.MIN_VALUE;
        int rightupY = Integer.MIN_VALUE;
        for(int[] rec : rectangles)
            int ldx = rec[0], ldy = rec[1], rux = rec[2], ruy = rec[3];
            area += (rux - ldx) * (ruy - ldy);
            leftdownX = Math.min(leftdownX, ldx);
            leftdownY = Math.min(leftdownY, ldy);
            rightupX = Math.max(rightupX, rux);
            rightupY = Math.max(rightupY, ruy);

            Point p1 = new Point(ldx, ldy);
            Point p2 = new Point(ldx, ruy);
            Point p3 = new Point(rux, ldy);
            Point p4 = new Point(rux, ruy);

            map.put(p1, map.getOrDefault(p1, 0) + 1);
            map.put(p2, map.getOrDefault(p2, 0) + 1);
            map.put(p3, map.getOrDefault(p3, 0) + 1);
            map.put(p4, map.getOrDefault(p4, 0) + 1);
        
        /*
        System.out.println(area);
        System.out.println(leftdownX);
        System.out.println(leftdownY);
        System.out.println(rightupX);
        System.out.println(rightupY);
        */
        //四个角的顶点
        Point ld = new Point(leftdownX, leftdownY);
        Point lu = new Point(leftdownX, rightupY);
        Point rd = new Point(rightupX, leftdownY);
        Point ru = new Point(rightupX, rightupY);
        //如果面积不相等，直接false
        if(area != (rightupY - leftdownY) * (rightupX - leftdownX))
            return false;
        //如果角出现了多次，那么fasle
        if(map.getOrDefault(ld, 0) != 1 || map.getOrDefault(lu, 0) != 1 || map.getOrDefault(rd, 0) != 1 || map.getOrDefault(ru, 0) != 1)
            return false;

        map.remove(ld);
        map.remove(lu);
        map.remove(rd);
        map.remove(ru);
        //判断其他点
        for(Map.Entry<Point, Integer> entry : map.entrySet())
            int count = entry.getValue();
            //如果不是出现了两次或者四次，那么就是false
            if(count != 2 && count != 4)
                return false;
        
        return true;
    


class Point
    int x;
    int y;

    public Point(int x, int y)
        this.x = x;
        this.y = y;
    

    public int hashCode()
        return x + y;
    

    public boolean equals(Object obj)
        if(this == obj)
            return true;
        if(obj == null)
            return false;
        if(obj instanceof Point)
            Point point = (Point)obj;
            return this.x == point.x && this.y == point.y;
        
        return false;
    

看三叶姐扫描线的做法
但是这个也需要发现这个题的特点，才能写出来这样的答案
三叶姐是将每个矩形用两条竖直方向的边（横坐标，竖直方向的下端点，竖直方向的上端点，是左边/右边的边）来表示，那么这样的话，左右两个边界的边就只有一条，而中间的边因为每个边会在两个矩形中出现，所以会出现两次

class Solution 
    public boolean isRectangleCover(int[][] rectangles) 
        //三叶姐的扫描线做法，将矩形用竖线表示
        //然后判断非边缘竖线是否出现两次，边缘竖线是否出现一次

        int n = rectangles.length;
        //先将所有边变成竖线
        int[][] rect = new int[n * 2][4];
        int idx = 0;
        for(int i = 0; i < n; i++)
            //当前矩形左边的边，1表示是右边的边
            rect[idx++] = new int[]rectangles[i][0], rectangles[i][1], rectangles[i][3], 1;
            rect[idx++] = new int[]rectangles[i][2], rectangles[i][1], rectangles[i][3], 0;
        
        Arrays.sort(rect, (a, b) ->(a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]));

        //然后对这些边进行合并
        int l = 2 * n;
        List<int[]> left = new ArrayList<>();   //左边的边，也就是flag为0的边
        List<int[]> right = new ArrayList<>();  //右边的边，也就是flag为1的边
        
        //开始扫描
        for(int i = 0; i < l; )
            int r = i;      //用一个新的变量代表右端点
            left.clear();
            right.clear();
            //找横坐标相同的部分
            while(r < l && rect[r][0] == rect[i][0])
                r++;
            //现在从i到r就是横坐标相同的部分    
            //放到list中进行拼接
            //注意rect是按照第二个下标从小到大排序的
            for(int j = i; j < r; j++)
                int[] cur = rect[j][1], rect[j][2];
                //找出此时是哪个list
                List<int[]> list = rect[j][3] == 0 ? left : right;
                //然后插入到这个list中，因为之前插入是按顺序来的，所以直接取出最上面的
                if(list.isEmpty())
                    list.add(cur);
                else
                    int[] last = list.get(list.size() - 1);
                    //如果这两个范围相交了，那么false
                    if(last[1] > cur[0])    
                        return false;
                    //如果是相连的，那么连接
                    else if(last[1] == cur[0])
                        last[1] = cur[1];
                    else
                        list.add(cur);
                    
                
            
            //插入完当前下标以后，判断是否是成对的
            if(i > 0 && r < l)
                if(left.size() != right.size())
                    return false;
                for(int j = 0; j < left.size(); j++)
                    if(left.get(j)[0] != right.get(j)[0] || left.get(j)[1] != right.get(j)[1])
                        return false;
                
            //如果是边缘的边，看是否是一条完整的边
            else
                if(left.size() + right.size() != 1)
                    return false;
            
            //将i置为r
            i = r;
           
        return true;
    

318. 最大单词长度乘积

2021.11.17 每日一题

题目描述

给定一个字符串数组 words，找到 length(word[i]) * length(word[j]) 的最大值，并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词，返回 0。

示例 1:

输入: [“abcw”,“baz”,“foo”,“bar”,“xtfn”,“abcdef”]
输出: 16
解释: 这两个单词为 “abcw”, “xtfn”。

示例 2:

输入: [“a”,“ab”,“abc”,“d”,“cd”,“bcd”,“abcd”]
输出: 4
解释: 这两个单词为 “ab”, “cd”。

示例 3:

输入: [“a”,“aa”,“aaa”,“aaaa”]
输出: 0
解释: 不存在这样的两个单词。

提示：

2 <= words.length <= 1000
1 <= words[i].length <= 1000
words[i] 仅包含小写字母

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-product-of-word-lengths
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

26位每一位表示对应字母是否存在
那个优化感觉作用不大

class Solution 
    public int maxProduct(String[] words) 
        //用26位表示每个单词中字母出现没有
        //然后异或来检查是否重复出现
        int n = words.length;
        int[] num = new int[n];
        for(int i = 0; i < n; i++)
            String s = words[i];
            for(char c : s.toCharArray())
                int t = c - 'a';
                num[i] |= (1 << t);
            
        
        int max = 0;
        for(int i = 0; i < n; i++)
            String s1 = words[i];
            for(int j  = i + 1; j < n; j++)
                String s2 = words[j];
                boolean flag = true;
                /*
                for(int k = 0; k < 26; k++)
                    if(((num[i] >> k) & 1) == 1 && (((num[j] >> k) & 1) == 1))
                        flag = false;
                        break;
                    
                
                */
                /*
                for(int t = num[i]; t > 0; t -= t & -t)
                    int temp = t & -t;
                    if((num[j] & temp) != 0)
                        flag = false;
                        break;
                    
                
                */
                if((num[i] & num[j]) == 0)
                    max = Math.max(max, s1.length() * s2.length());
            
        
        return max;
    

563. 二叉树的坡度

2021.11.18 每日一题

题目描述

给定一个二叉树，计算 整个树 的坡度 。

一个树的 节点的坡度 定义即为，该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话，左子树的节点之和为 0 ；没有右子树的话也是一样。空结点的坡度是 0 。

整个树 的坡度就是其所有节点的坡度之和。

示例 1：

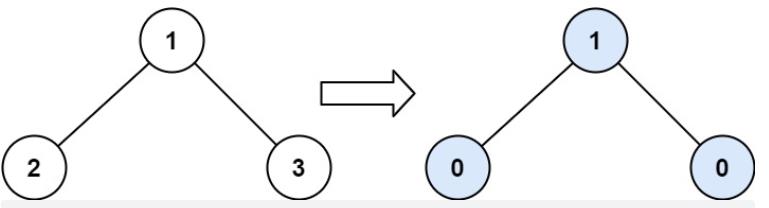
输入：root = [1,2,3]
输出：1
解释：
节点 2 的坡度：|0-0| = 0（没有子节点）
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 1 的坡度：|2-3| = 1（左子树就是左子节点，所以和是 2 ；右子树就是右子节点，所以和是 3 ）
坡度总和：0 + 0 + 1 = 1

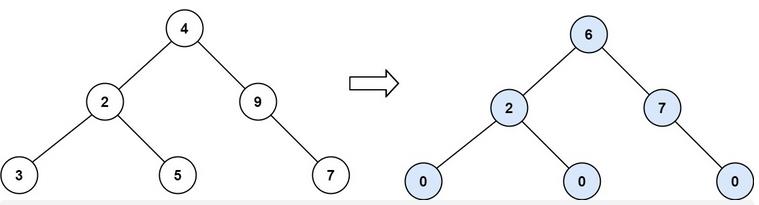
示例 2：

输入：root = [4,2,9,3,5,null,7]
输出：15
解释：
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 5 的坡度：|0-0| = 0（没有子节点）
节点 7 的坡度：|0-0| = 0（没有子节点）
节点 2 的坡度：|3-5| = 2（左子树就是左子节点，所以和是 3 ；右子树就是右子节点，所以和是 5 ）
节点 9 的坡度：|0-7| = 7（没有左子树，所以和是 0 ；右子树正好是右子节点，所以和是 7 ）
节点 4 的坡度：|(3+5+2)-(9+7)| = |10-16| = 6（左子树值为 3、5 和 2 ，和是 10 ；右子树值为 9 和 7 ，和是 16 ）
坡度总和：0 + 0 + 0 + 2 + 7 + 6 = 15

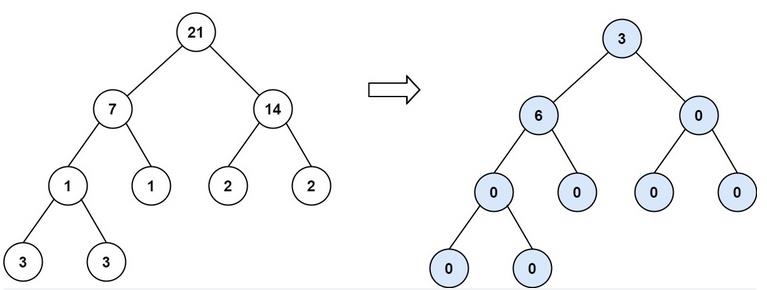
示例 3：

输入：root = [21,7,14,1,1,2,2,3,3]
输出：9

提示：

树中节点数目的范围在 [0, 104] 内
-1000 <= Node.val <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-tilt
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

一个简单的二叉树后序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode 
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() 
 *     TreeNode(int val)  this.val = val; 
 *     TreeNode(int val, TreeNode left, TreeNode right) 
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     
 * 
 */
class Solution 
    int sum = 0;
    public int findTilt(TreeNode root) 
        //坡度，后序遍历吧
        dfs(root);
        return sum;
    
    
    public int dfs(TreeNode root)
        if(root == null)
            return 0;
        int left = dfs(root.left);
        int right = dfs(root.right);
        int po = Math.abs(left - right);
        sum += po;
        return left + right + root.val;