排序算法补充总结(非比较排序)
Posted ohana!
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了排序算法补充总结(非比较排序)相关的知识,希望对你有一定的参考价值。
目录
一,海量排序问题
1.基本情况
当数据量非常庞大时,但是,内存只有1G,4G等等情况下,插入,交换,选择排序算法都只能把数据加载到内存去进行,此时,解决问题的方法就比较难了,但是也不是没有办法,我们可以使用归并排序,它的应用场景多是针对外部排序
- 外部排序:排序过程需要在磁盘等外部存储进行的排序
2.场景举例
此时有20个G的数据需要我们去进行排序,但是我们的计算机的内存只有4G,明显是内部排序不能满足的情况(就算全部让内存来运行排序也不行,实际情况是,计算机的操作系统,还有别的计算机的软件要同时运行,所以,内存是绝对不行的)
3.解决思路(解决办法)
- 先把文件切分成40份,每个512M
- 分别对512 M排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行40路归并,同时对40份有序文件做归并过程,最终结果就有序了
二,计数排序(非比较排序)
1.基本思想(实现思路)
- 先对原数组出现元素的次数进行记录(创建一个新的数组)
- 根据统计的结果,将数据还原到原来的数组当中
2.实现代码
public static void countSort(int[] array)
//先统计原来数组的元素进行处理----数据集中在某一个区间当中
//就用最大值减去最小值在加一就是统计数组的长度
int max = 0;
int min = 0;
for (int i = 0; i < array.length; i++)
//找最大元素的下标
if(array[i] > array[max])
max = i;
//找最小元素的下标
if(array[i] < array[min])
min = i;
//对原数组最大,最小的元素作差加一得到统计数组的长度
int len = array[max] - array[min] + 1;
int Min = array[min];
//定义统计数组(用数组的值作为统计数组的下标)
int[] arr = new int[len];
for (int i = 0; i < array.length; i++)
arr[array[i] - Min]++;
//这个j定义的实际上是原数组的下标,届时如果有相同的元素
//那么统计数组的下标必然不会变,因此就需要我们定义一个下标来控制原数组的下标进行移动
int j = 0;
for (int i = 0; i < arr.length; i++)
//还原原数组
int index = arr[i];
//index控制同一个元素的连续传递给原数组
while(index != 0)
//需要注意的是,我们要对这个i再加上Min,因为,当时计算时是减去了最小值
array[j] = i + Min;
index--;
j++;
3.性能分析
(1)时间复杂度:
- 从一个层面来说,最坏的情况是外层循环走满,那么,这样内层循环就可以忽略,因此时间复杂度是O(N)
(2)空间复杂度:
- 因为向外接住了一段辅助空间,但是,数组长度又不全是原数组的长度,不一定是O(N),视具体情况而定
(3)稳定性:
- 稳定
(4)适用场景:
- 适合于数据集中于某一个区间的时候
4.测试
public class CountSort
public static void countSort(int[] array)
//先统计原来数组的元素进行处理----数据集中在某一个区间当中
//就用最大值减去最小值在加一就是统计数组的长度
int max = 0;
int min = 0;
for (int i = 0; i < array.length; i++)
//找最大元素的下标
if(array[i] > array[max])
max = i;
//找最小元素的下标
if(array[i] < array[min])
min = i;
//对原数组最大,最小的元素作差加一得到统计数组的长度
int len = array[max] - array[min] + 1;
int Min = array[min];
//定义统计数组(用数组的值作为统计数组的下标)
int[] arr = new int[len];
for (int i = 0; i < array.length; i++)
arr[array[i] - Min]++;
//这个j定义的实际上是原数组的下标,届时如果有相同的元素
//那么统计数组的下标必然不会变,因此就需要我们定义一个下标来控制原数组的下标进行移动
int j = 0;
for (int i = 0; i < arr.length; i++)
//还原原数组
int index = arr[i];
//index控制同一个元素的连续传递给原数组
while(index != 0)
//需要注意的是,我们要对这个i再加上Min,因为,当时计算时是减去了最小值
array[j] = i + Min;
index--;
j++;
public static void print(int[] array)
for (int i = 0; i < array.length; i++)
System.out.print(array[i] + " ");
System.out.println();
public static void main(String[] args)
int[] array = 9,9,7,7,0,4,3,2,0,0;
print(array);
countSort(array);
print(array);
三,桶排序(简单了解)
- 桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
- 同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要
1. 什么时候最快
当输入的数据可以均匀的分配到每一个桶中
2. 什么时候最慢
当输入的数据被分配到了同一个桶中
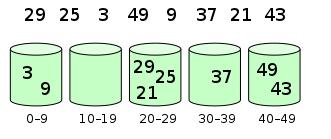
3. 示意图
元素分布在桶中:
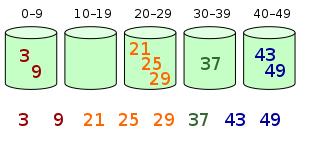
然后,元素在每个桶中排序:
以上是关于排序算法补充总结(非比较排序)的主要内容,如果未能解决你的问题,请参考以下文章