AcWing 291. 蒙德里安的梦想(状态压缩dp模板)

Posted 2021-12-14 卷王2048

AcWing 291. 蒙德里安的梦想(状态压缩dp模板)

题目

291. 蒙德里安的梦想 - AcWing题库

求把 N×M 的棋盘分割成若干个 1×2 的的长方形，有多少种方案。

例如当 N=2，M=4时，共有 55 种方案。当 N=2，M=3 时，共有 33 种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 N和 M。

当输入用例 N=0，M=0时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

1≤N,M≤11

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

题解

思路：

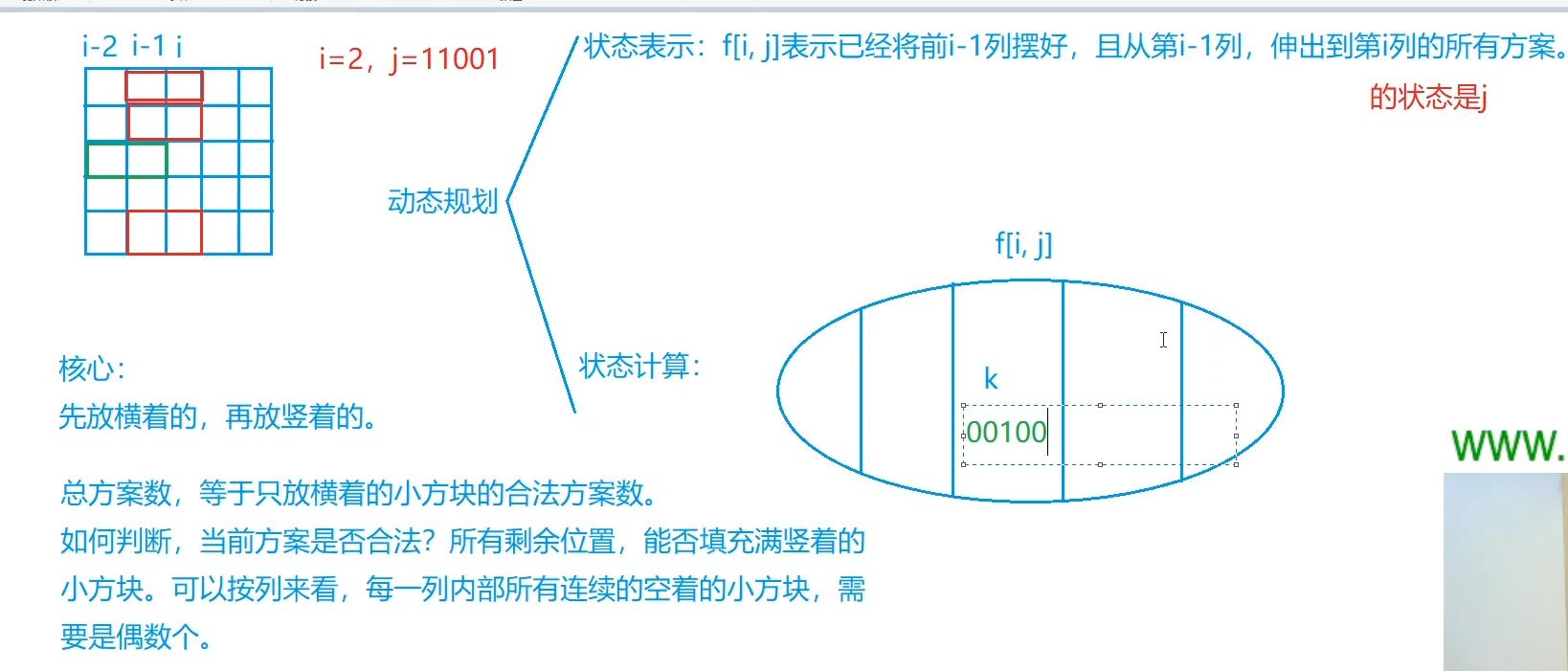
与其他状态压缩dp按行递推不同，本题是按列向后递推的

dp[i][j]表示已经填完前i列，且第i列的状态为j的方案数

枚举第i-1列的状态，找到所有符合的情况

Python代码

N = 12
dp = [[0]*(1<<N) for _ in range(N)]
st = [False]*(1<<N)


while True:
    n,m = map(int ,input().split())
    if n==0 or m==0:break
    
    #预处理一列的所有可能状态
    for i in range(1<<n):
        #cnt表示本列当前连续的空格子的数量
        cnt = 0
        st[i] = True
        #一位一位的判断每个状态
        for j in range(n):
            if i>>j&1:
                # cnt&1; 等价于cnt%2!=0，即当前有奇数个空格子，就不能竖着放满方块
                if cnt&1:
                    st[i] = False
                cnt = 0
            else:
                cnt+=1
        #遍历完所有后剩下奇数个格子，则该状态不合法
        if cnt&1:
            st[i] = False

    #因为是多组数据，每一组数据用之前都要把上一次的记录清空
    dp = [[0]*(1<<n+1) for _ in range(m+1)]
    
    dp[0][0] = 1
    #枚举每一列
    for i in range(1,m+1):
        #枚举第i列的所有状态
        for j in range(1<<n):
            #枚举第i-1列的所有状态
            for k in range(1<<n):
                #判断两列匹配是否合法
                if j&k==0 and st[j|k]:
                    dp[i][j]+=dp[i-1][k]
    print(dp[m][0])
# print(st)
    
    

    if j&k==0 and st[j|k]:
                dp[i][j]+=dp[i-1][k]
print(dp[m][0])

print(st)