Acwing292. 炮兵阵地(网格型状态压缩dp)

Posted 2021-12-14 卷王2048

Acwing292. 炮兵阵地(网格型状态压缩dp)

题目

司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。

一个 N×M 的地图由 N 行 M 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

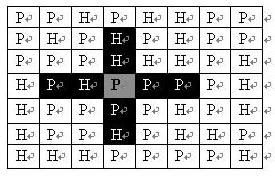
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 N 和 M；

接下来的 N 行，每一行含有连续的 M 个字符(P 或者 H)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数 K，表示最多能摆放的炮兵部队的数量。

数据范围

N≤100,M≤10

输入样例：

5 4
phpP
PPHH
PPPP
PHPP
PHHP

输出样例：

6

题解(Python)

写法一：

仿照327. 玉米田 的写法

N, M = 105, 12
n, m = map(int, input().split())
dp = [[[0] * (1 << m) for _ in range(1 << m)] for _ in range(2)]
state, pre = [], [[] for _ in range(1 << m)]
cnt = [0]*(1<<m)
g = [0] * N

# 读入地图,并压缩
for i in range(1, n + 1):
    row = input()
    for j in range(m):
        if row[j] == 'H':
            g[i] += 1 << j


# 判断是否合法的函数
def check(x):
    for i in range(m):
        if x >> i & 1 and (x >> i + 1 & 1 or x >> i + 2 & 1):
            return False
    return True

def count(x):
    ans = 0
    for i in range(m):
        if (x>>i&1)==1:
            ans+=1
    return ans

# 预处理所有状态
for i in range(1 << m):
    if check(i):
        state.append(i)
        cnt[i] = count(i)

# 存下所有合法状态
for i in state:
    for j in state:
        if i & j == 0:
            pre[i].append(j)

# dp过程
for i in range(1, n + 1):
    for st in state:
        if g[i] & st == 0:
            for a in pre[st]:
                for b in pre[a]:
                    if st & b==0:
                        dp[i & 1][st][a] = max(dp[i & 1][st][a], dp[i - 1 & 1][a][b] + cnt[st])
res = 0
for st in state:
    for i in pre[st]:
        res = max(res, dp[n & 1][st][i])
#         print(dp[n & 1][st][i],end = " ")
print(res)
# print(g)
# print(state)

写法二：

y总写法

N, M = 105, 12
n, m = map(int, input().split())
dp = [[[0] * (1<<m) for _ in range(1<<m)] for _ in range(2)]
state = []
cnt = [0]*(1<<m)
g = [0] * N

# 读入地图,并压缩
for i in range(1, n + 1):
    row = input()
    for j in range(m):
        if row[j] == 'H':
            g[i] += 1 << j


# 判断是否合法的函数
def check(x):
    for i in range(m):
        if x >> i & 1 and (x >> i + 1 & 1 or x >> i + 2 & 1):
            return False
    return True

def count(x):
    ans = 0
    for i in range(m):
        if (x>>i&1)==1:
            ans+=1
    return ans

# 预处理所有状态
for i in range(1 << m):
    if check(i):
        state.append(i)
        cnt[i] = count(i)

# # 存下所有合法状态
# for i in state:
#     for j in state:
#         if i & j == 0:
#             pre[i].append(j)

# dp过程
for i in range(1, n + 1):
    for j in range(len(state)):
        for k in range(len(state)):
            for u in range(len(state)):
                a,b,c = state[j],state[k],state[u]
                if a&b!=0 or a&c!=0 or b&c!=0: continue
                if (g[i]&a)!=0 or (g[i-1]&b)!=0:continue
                dp[i & 1][j][k] = max(dp[i & 1][j][k], dp[i - 1 & 1][k][u] + cnt[a]);
        
        
res = 0
for i in range(len(state)):
    for j in range(len(state)):
        res = max(res, dp[n & 1][i][j])

print(res)

题解(c++和Java)

直接去欣赏大佬的博客

c++

AcWing 292. 炮兵阵地【线性状压DP+常规优化+转移优化】 - AcWing

Java

AcWing 292. 炮兵阵地 - AcWing