实验1 最小生成树问题Kruskal+Prim

Posted 2021-12-14 Roninaxious

1.贪心算法思想

贪心算法的基本思想是找出整体当中每个小的局部的最优解，并且将所有的这些局部最优解合起来形成整体上的一个最优解。因此能够使用贪心算法的问题必须满足下面的两个性质：

• 1.整体的最优解可以通过局部的最优解来求出；
• 2.一个整体能够被分为多个局部，并且这些局部都能够求出最优解。

2.贪心算法的基本策略 ：

1、从问题的某个初始解出发。
2、采用循环语句，当可以向求解目标前进一步时，就根据局部最优策略，得到一个部分解，缩小问题的范围或规模。
3、将所有部分解综合起来，得到问题的最终解。

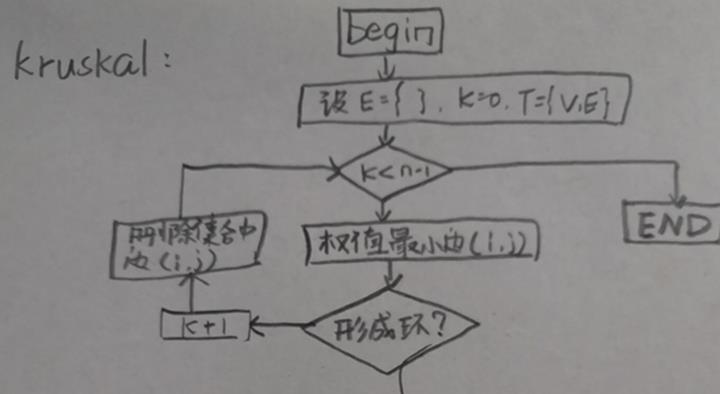
(2-1)Kruskal算法

• 将所有边按照权值的大小进行升序排序，然后从小到大一一判断，条件为：如果这个边不会与之前选择的所有边组成回路，就可以作为最小生成树的一部分；反之，舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。

(2-2)Prim算法

• Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中。

3.数据结构
Prim算法：

• a. 在一个加权连通图中，顶点集合V，边集合为E
• b. 任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离，选择距离最短的，标记visit.
• c. 重复以下操作，直到所有点都被标记为visit：
  在剩下的点钟，计算与已标记visit点距离最小的点，标记visit,证明加入了最小生成树。

Kruskal算法

• a.假定拓扑图的边的集合是E，初始化最小生成树边集合G=。
• b. 遍历集合E中的所有元素，并且按照权值的大小进行排序。
• c. 找出E中权值最小的边e 。
• d .如果边e不和最小生成树集合G中的边构成环路，则将边e加到边集合G中；否则测试下一条权值次小的边，直到满足条件为止。
• e. 重复步骤b，直到G=E。

4.数据模型

5.程序代码
Kruskal算法Java代码实现

public class Kruskal 
    public int edgeNums;                           //边的数量
    public char[] data;                             //存储结点
    public int[][] matrix;                          //邻接矩阵存储权重
    private static final int INF = Integer.MAX_VALUE; //表示结点不通

    public Kruskal(char[] data, int[][] matrix) 
        int length = data.length;
        this.data = new char[length];
        this.matrix = new int[length][length];
        for (int i = 0; i < length; i++) 
            this.data[i] = data[i];
        
        for (int s = 0; s < length; s++) 
            for (int k = 0; k < length; k++) 
                this.matrix[s][k] = matrix[s][k];
            
        
        for (int m = 0; m < length; m++) 
            for (int n = m + 1; n < length; n++) 
                if (matrix[m][n] != INF) 
                    this.edgeNums++;
                
            
        
    

    /**
     * 将遍历邻接矩阵将边加入到Edge数组中
     *
     * @return Edge数组
     */
    public Edge[] getEdges() 
        int length = this.data.length;
        int index = 0;
        Edge[] edges = new Edge[this.edgeNums];
        for (int m = 0; m < length; m++) 
            for (int n = m + 1; n < length; n++) 
                if (matrix[m][n] != INF) 
                    edges[index] = new Edge(data[m], data[n], matrix[m][n]);
                    index++;
                
            
        
        return edges;
    

    /**
     * 对Edge数组进行排序
     *
     * @param edges 数组引用
     */
    public void sortEdges(Edge[] edges) 
        for (int k = 0; k < edges.length - 1; k++) 
            for (int s = 0; s < edges.length - k - 1; s++) 
                if (edges[s].weight > edges[s + 1].weight) 
                    Edge temp = edges[s];
                    edges[s] = edges[s + 1];
                    edges[s + 1] = temp;
                
            
        
    

    /**
     * 克鲁斯卡尔核心方法
     * 流程：
     * 1.将图中的边放到集合中
     * 2.边排序   - 》 权重  T集合
     * 3.对T集合进行遍历
     * T
     */
    public void kruskal() 
        Edge[] edges = getEdges();
        sortEdges(edges);
        Edge[] result = new Edge[edgeNums];
        int[] ends = new int[edgeNums];
        int index = 0;
        for (int k = 0; k < edgeNums; k++) 
            int front = getPosition(edges[k].front);
            int after = getPosition(edges[k].after);
            int m = getEnd(ends, front);
            int n = getEnd(ends, after);
            if (m != n) 
                ends[m] = n;
                result[index++] = edges[k];
            
        
        System.out.println(Arrays.toString(result));
    

    /**
     * 得到末尾的结点
     *
     * @param ends 存储
     * @param k    元素下标
     * @return 返回元素
     */
    public int getEnd(int[] ends, int k) 
        while (ends[k] != 0) 
            k = ends[k];
        
        return k;
    

    /**
     * 获取元素对于的下标
     *
     * @param ch 待查询字符
     * @return 下标
     */
    private int getPosition(char ch) 
        for (int i = 0; i < data.length; i++) 
            if (data[i] == ch) 
                return i;
            
        
        return -1;
    

    public void printMatrix() 
        System.out.println("二维矩阵列表为:");
        for (int[] cur : matrix) 
            System.out.println(Arrays.toString(cur));
        
        System.out.println("边的大小为:" + this.edgeNums);

    
    / /main测试
    public static void main(String[] args) 
        char[] vertex = 'A', 'B', 'C', 'D', 'E', 'F', 'G';
        int[][] matrix = 
                0, 12, INF, INF, INF, 16, 14,
                12, 9, 10, INF, INF, 7, INF,
                INF, 10, 0, 3, 5, 6, INF,
                INF, INF, 3, 0, 4, INF, INF,
                INF, INF, 5, 4, 0, 2, 8,
                16, 7, 6, INF, 2, 0, 9,
                14, INF, INF, INF, 8, 9, 0
        ;
        Kruskal kruskal = new Kruskal(vertex, matrix);
        kruskal.printMatrix();
        kruskal.kruskal();
    


class Edge 
    public char front;
    public char after;
    public int weight;

    public Edge(char front, char after, int weight) 
        this.front = front;
        this.after = after;
        this.weight = weight;
    

    @Override
    public String toString() 
        return "Edge" +
                "front=" + front +
                ", after=" + after +
                ", weight=" + weight +
                '';
    


Prim算法Java代码实现
public class Prim 
    public static void main(String[] args) 
        char[] data = 'A', 'B', 'C', 'D', 'E', 'F', 'G';
        int nodes = data.length;
        int[][] weight = 
                10000, 5, 7, 10000, 10000, 10000, 2,
                5, 10000, 10000, 9, 10000, 10000, 3,
                7, 10000, 10000, 10000, 8, 10000, 10000,
                10000, 9, 10000, 10000, 10000, 4, 10000,
                10000, 10000, 8, 10000, 10000, 5, 4,
                10000, 10000, 10000, 4, 5, 10000, 6,
                2, 3, 10000, 10000, 4, 6, 10000,
        ;
        MinTree minTree = new MinTree();
        Graph graph = new Graph(nodes);
        minTree.createGraph(nodes, data, weight, graph);
        minTree.showGraph(graph);
        minTree.prim(graph, 0);
    


class MinTree 
    /**
     * 初始化无向图
     * @param nodes 结点数
     * @param data  结点数组
     * @param weight 权重邻接矩阵
     * @param graph  无向图
     */
    public void createGraph(int nodes, char[] data, int[][] weight, Graph graph) 
        int i, j;
        for (i = 0; i < nodes; i++) 
            graph.data[i] = data[i];
            for (j = 0; j < nodes; j++) 
                graph.weight[i][j] = weight[i][j];
            
        
    

    /**
     * 最小生成树问题
     * 1.给定一个无向连通图，如果选取生成一棵树，使得树上所有的权总和最小，这就是最小生成树
     * 2.给定n个结点，一定有n-1条边
     * 两种算法 1.普里姆算法  和  克鲁斯卡尔算法
     * @param graph  邻接图
     * @param v      开始结点的下标
     *
     *  1.创建V集合保存结点    ---  遍历
     *  2.从某个结点出发， 每次取出 A  E  T
     */
    public void prim(Graph graph, int v) 
        int x1 = -1, x2 = -1;
        int nodeNums = graph.nodes;
        int[] visited = new int[nodeNums];
        visited[v] = 1;
        int minWeight = 10000;               //先自定义最大权重，后面替换
        for (int k = 1; k < nodeNums; k++)     //n个结点需要n-1条边
            for (int al = 0; al < nodeNums; al++)     //已经标记的
                for (int not = 0; not < nodeNums; not++)   //未标记的
                    if (visited[al] == 1 && visited[not] == 0 && graph.weight[al][not] < minWeight) 
                        minWeight = graph.weight[al][not];
                        x1 = al;
                        x2 = not;
                    
                
            
            visited[x2] = 1;
            minWeight = 10000;
            System.out.println("边<"+graph.data[x1]+"-"+graph.data[x2]+">"+"权值为:"+graph.weight[x1][x2]);
        

    
    //显示邻接矩阵
    public void showGraph(Graph graph) 
        for (int[] cur : graph.weight) 
            System.out.println(Arrays.toString(cur));
        
    


class Graph 
    protected int nodes;          //结点的个数
    protected char[] data;         //结点的数据
    protected int[][] weight;     //结点的邻接矩阵

    public Graph(int nodes) 
        this.nodes = nodes;
        data = new char[nodes];
        weight = new int[nodes][nodes];
    

6.测试
（1）Kruskal算法测试数据如下

(其中的INF表示两顶点之间不通)

控制台结果如下：

（2）Prim算法测试数据如下：

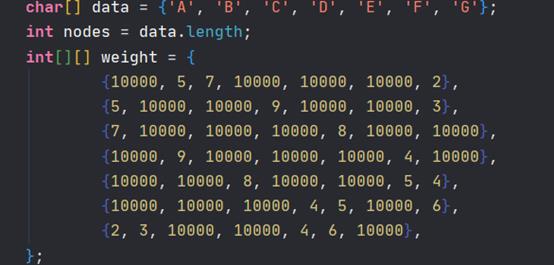
(1000表示两个顶点不连通,也可也和上面的Kruskal算法一样使用int的最大值65535表示)
控制台结果如下：

7.结果分析:
Prim
通过邻接矩阵图表示的简易实现中，找到所有最小权边共需O（V）的运行时间。使用简单的二叉堆与邻接表来表示的话，普里姆算法的运行时间则可缩减为O(ElogV)，其中E为连通图的边数，V为顶点数。如果使用较为复杂的斐波那契堆，则可将运行时间进一步缩短为O(E+VlogV)，这在连通图足够密集时，可较显著地提高运行速度

Kruskal
克鲁斯卡尔算法的时间复杂度主要由排序方法决定，而克鲁斯卡尔算法的排序方法只与网中边的条数有关，而与网中顶点的个数无关，当使用时间复杂度为O（elog2e）的排序方法时，克鲁斯卡尔算法的时间复杂度即为O（log2e），因此当网的顶点个数较多、而边的条数较少时，使用克鲁斯卡尔算法构造最小生成树效果较好