一文搞懂深度网络初始化(Xavier and Kaiming initialization)
Posted 魏晓蕾
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一文搞懂深度网络初始化(Xavier and Kaiming initialization)相关的知识,希望对你有一定的参考价值。
本文以MNIST手写体数字识别模型为例来演示参数初始化对模型训练的影响。点击这里查看源码。
Xavier Initialization
早期的参数初始化方法普遍是将数据和参数normalize为高斯分布(均值0方差1),但随着神经网络深度的增加,这方法并不能解决梯度消失问题。
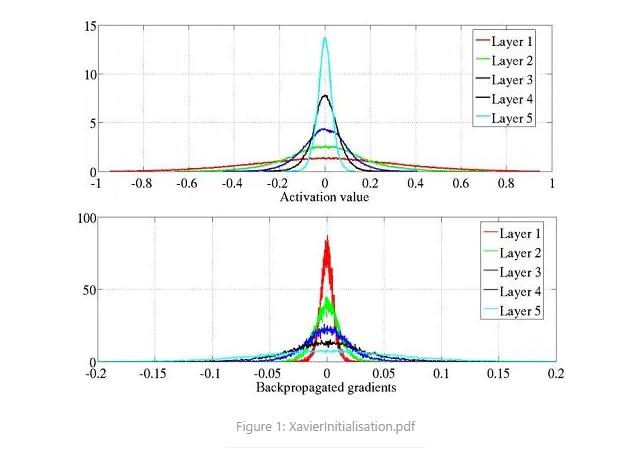
Xavier初始化的作者,Xavier Glorot,在Understanding the difficulty of training deep feedforward neural networks论文中提出一个洞见:激活值的方差是逐层递减的,这导致反向传播中的梯度也逐层递减。要解决梯度消失,就要避免激活值方差的衰减,最理想的情况是,每层的输出值(激活值)保持高斯分布。
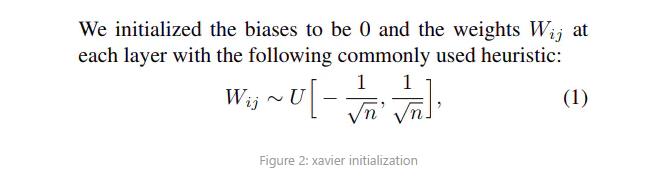
因此,他提出了Xavier初始化:bias初始化为0,为Normalize后的参数乘以一个rescale系数: 1 / n 1/\\sqrt n 1/n,n是输入参数的个数。
公式的推导过程大致如下:

如果上述这段公式你看晕了,也没关系,只要记住结果就好。
接下来,我们要做实验来验证Xavier的洞见。
def linear(x, w, b): return x @ w + b
def relu(x): return x.clamp_min(0.)
nh = 50
W1 = torch.randn(784, nh)
b1 = torch.zeros(nh)
W2 = torch.randn(nh, 1)
b2 = torch.zeros(1)
z1 = linear(x_train, W1, b1)
print(z1.mean(), z1.std())
tensor(-0.8809) tensor(26.9281)
这是个简单的线性回归模型: y = a x + b y=ax+b y=ax+b,(W1, b1)和(W2, b2)分别是隐层和输出层的参数,W1/W2初始化为高斯分布,b1/b2初始为0。果然,第一个linear层的输出值(z1)的均值和标准差就已经发生了很大的变化。如果后续使用sigmoid作为激活函数,那梯度消失就会很明显。
现在我们按照Xavier的方法来初始化参数:
W1 = torch.randn(784, nh) * math.sqrt(1 / 784)
b1 = torch.zeros(nh)
W2 = torch.randn(nh, 1) * math.sqrt(1 / nh)
b2 = torch.zeros(1)
z1 = linear(x_train, W1, b1)
print(z1.mean(), z1.std())
tensor(0.1031) tensor(0.9458)
a1 = relu(z1)
a1.mean(), a1.std()
(tensor(0.4272), tensor(0.5915))
参数经过Xavier初始化后,linear层的输出值的分布没有大的变化(U[0.1031, 0.9458]),依旧接近高斯分布,但是好景不长,relu的激活值分布就开始跑偏了(U[0.4272, 0.5915])。
Kaiming Initialization
Xavier初始化的问题在于,它只适用于线性激活函数,但实际上,对于深层神经网络来说,线性激活函数是没有价值,神经网络需要非线性激活函数来构建复杂的非线性系统。今天的神经网络普遍使用relu激活函数。
Kaiming初始化的发明人kaiming he,在Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification论文中提出了针对relu的kaiming初始化。
因为relu会抛弃掉小于0的值,对于一个均值为0的data来说,这就相当于砍掉了一半的值,这样一来,均值就会变大,前面Xavier初始化公式中E(x)=mean=0的情况就不成立了。根据新公式的推导,最终得到新的rescale系数: 2 / n \\sqrt 2/n 2/n。更多细节请看论文的section 2.2。
W1 = torch.randn(784, nh) * math.sqrt(2 / 784)
b1 = torch.zeros(nh)
W2 = torch.randn(nh, 1) * math.sqrt(2 / nh)
b2 = torch.zeros(1)
z1 = linear(x_train, W1, b1)
a1 = relu(z1)
a1.mean(), a1.std()
(tensor(0.4553), tensor(0.7339))
可以看到,Kaiming初始化的表现要优于Xavier初始化,relu之后的输出值标准差还有0.7339(浮动可以达到0.8+)。
实际上,Kaiming初始化已经被Pytorch用作默认的参数初始化函数。
import torch.nn.init as init
W1 = torch.zeros(784, nh)
b1 = torch.zeros(nh)
W2 = torch.zeros(nh, 1)
b2 = torch.zeros(1)
init.kaiming_normal_(W1, mode='fan_out', nonlinearity='relu')
init.kaiming_normal_(W2, mode='fan_out')
z1 = linear(x_train, W1, b1)
a1 = relu(z1)
print("layer1: ", a1.mean(), a1.std())
z2 = linear(a1, W2, b2)
layer1: tensor(0.5583) tensor(0.8157)
tensor(1.1784) tensor(1.3209)
现在,方差的问题已经解决了,接下来就是均值不为0的问题。因为在x轴上平移data并不会影响data的方差,因此,如果把relu的激活值左移5,结果会如何?
def linear(x, w, b):
return x @ w + b
def relu(x):
return x.clamp_min(0.) - 0.5
def model(x):
x = relu(linear(x, W1, b1))
print("layer1: ", x.mean(), x.std())
x = relu(linear(x, W2, b2))
print("layer2: ", x.mean(), x.std())
x = linear(x, W3, b3)
print("layer3: ", x.mean(), x.std())
return x
nh = [100, 50]
W1 = torch.zeros(784, nh[0])
b1 = torch.zeros(nh[0])
W2 = torch.zeros(nh[0], nh[1])
b2 = torch.zeros(nh[1])
W3 = torch.zeros(nh[1], 1)
b3 = torch.zeros(1)
init.kaiming_normal_(W1, mode='fan_out')
init.kaiming_normal_(W2, mode='fan_out')
init.kaiming_normal_(W3, mode='fan_out')
_ = model(x_train)
layer1: tensor(0.0383) tensor(0.7993)
layer2: tensor(0.0075) tensor(0.7048)
layer3: tensor(-0.2149) tensor(0.4493)
结果出乎意料的好,这个三层的模型在没有添加batchnorm的情况下,每层的输入值和输出值都接近高斯分布,虽然数据方差是会逐层递减,但相比normalize初始化和Xavier初始化要好很多。
最后,因为Kaiming初始化是pytorch的默认初始化函数,因此我又用pytorch提供的nn.Linear()和nn.Relu()来构建相同的模型对比测试,结果是大跌眼镜。
class Model(nn.Module):
def __init__(self):
super().__init__()
self.lin1 = nn.Linear(784, nh[0])
self.lin2 = nn.Linear(nh[0], nh[1])
self.lin3 = nn.Linear(nh[1], 1)
self.relu = nn.ReLU()
def forward(self, x):
x = self.relu(self.lin1(x))
print("layer 1: ", x.mean().item(), x.std().item())
x = self.relu(self.lin2(x))
print("layer 2: ", x.mean().item(), x.std().item())
x = self.relu(self.lin3(x))
print("layer 3: ", x.mean().item(), x.std().item())
return x
m = Model()
_ = m(x_train)
layer 1: 0.2270725518465042 0.32707411050796
layer 2: 0.033514849841594696 0.23475737869739532
layer 3: 0.013271240517497063 0.09185370802879333
可以看到,第三层的输出已经均值为0、方差为0。去看nn.Linear()类的代码时会看到,它在做初始化时会传入参数 a = m a t h . s q r t ( 5 ) a=math.sqrt(5) a=math.sqrt(5)。我们知道,当输入为负数时,leaky relu的梯度为 [ 0 , ∞ ] [0,\\infty] [0,∞], x = λ x x=\\lambda x x=λx,参数 a a a就是这个 λ \\lambda λ。虽然kaiming_uniform_()的默认网络要使用的激活函数是leaky relu,但a默认值为0,此时leaky relu就等于relu。但现在数据存在负数,因此,mean相比relu模型更接近于0,甚至 E ( x ) > 0 E(x) > 0 E(x)>0的假设都不成立了,因此,rescale系数就不准确了,nn.Linear()才会有这样的表现。
def reset_parameters(self):
init.kaiming_uniform_(self.weight, a=math.sqrt(5))
END
本文通过Xavier和Kaiming初始化来展现了参数初始化的重要性,因为糟糕的初始化容易让神经网络陷入梯度消失的陷阱中。
以上是关于一文搞懂深度网络初始化(Xavier and Kaiming initialization)的主要内容,如果未能解决你的问题,请参考以下文章