树的直径和LCA
Posted Harris-H
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了树的直径和LCA相关的知识，希望对你有一定的参考价值。
树的直径和LCA
图中所有最短路径的最大值即为「直径」，可以用两次 DFS 或者树形 DP 的方法在 O(n) 时间求出树的直径。
方法1
首先对任意一个结点做 DFS 求出最远的结点，然后以这个结点为根结点再做 DFS 到达另一个最远结点。第一次 DFS 到达的结点可以证明一定是这个图的直径的一端，第二次 DFS 就会达到另一端。下面来证明这个定理。
两次DFS的方法不适用于有负权边的树。
const int N = 10000 + 10;
int n, c, d[N];
vector<int> E[N];
void dfs(int u, int fa)
for (int v : E[u])
if (v == fa) continue;
d[v] = d[u] + 1;
if (d[v] > d[c]) c = v;
dfs(v, u);
int main()
scanf("%d", &n);
for (int i = 1; i < n; i++)
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
dfs(1, 0);
d[c] = 0, dfs(c, 0);
printf("%d\\n", d[c]);
return 0;
方法2
const int N = 10000 + 10;
int n, d = 0;
int d1[N], d2[N];
vector<int> E[N];
void dfs(int u, int fa)
d1[u] = d2[u] = 0;
for (int v : E[u])
if (v == fa) continue;
dfs(v, u);
int t = d1[v] + 1;
if (t > d1[u])
d2[u] = d1[u], d1[u] = t;
else if (t > d2[u])
d2[u] = t;
d = max(d, d1[u] + d2[u]);
int main()
scanf("%d", &n);
for (int i = 1; i < n; i++)
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
dfs(1, 0);
printf("%d\\n", d);
return 0;
总结
方法1根据定理：从任意点出发到达的最远点必然是直径的一个端点，然后从该点出发到达的最远距离就是直径，即两次 d f s dfs dfs即可。
方法2根据树形dp：维护每个点的最大值和次大值，然后 a n s = m a x ( a n s , d 1 [ u ] + d 2 [ u ] ) ans=max(ans,d_1[u]+d_2[u]) ans=max(ans,d1[u]+d2[u])即可 。
二、LCA
性质
倍增LCA
//倍增LCA
int n;
struct edge
int to,nt;
e[N<<1];
int h[N],cnt,f[N][21],dep[N];
void add(int u,int v)
e[++cnt]=v,h[u],h[u]=cnt;
e[++cnt]=u,h[v],h[v]=cnt;
void dfs(int u)
for(int i=h[u];i;i=e[i].nt)
int v=e[i].to;
if(v!=f[u][0])
f[v][0]=u;
dep[v]=dep[u]+1;
dfs(v);
void init()
for(int j=1;j<=20;j++)
for(int i=1;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1];
int lca(int u,int v)
if(dep[u]<dep[v]) swap(u,v);
int delta=dep[u]-dep[v];
for(int i=0;i<=20;i++)
if(delta>>i&1) u=f[u][i];
if(u==v) return u;
for(int i=20;~i;i--)
if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
return f[u][0];
tarjanLCA
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a,b) memset(a,b,sizeof a)
#define PII pair<int,int>
#define fi first
#define se second
#define pb push_back
int h[N],h1[N],cnt1,cnt2;
int n,m,st,q;
int s[N],vis[N];
int find(int x) //查找
return s[x]==x?x:s[x]=find(s[x]);
inline void merge(int x,int y) //合并
x=find(x),y=find(y);
if(x!=y) s[y]=x;
struct node
int to,nt,lca;
e[N<<1],e1[N<<1];
inline void add(int u,int v) //建图
e[++cnt1]=v,h[u],h[u]=cnt1;
e[++cnt1]=u,h[v],h[v]=cnt1;
inline void add1(int u,int v) //询问边建图
e1[++cnt2]=v,h1[u],h1[u]=cnt2;
e1[++cnt2]=u,h1[v],h1[v]=cnt2;
void dfs(int u) //dfs
s[u]=u,vis[u]=1;
for(int i=h[u];i;i=e[i].nt)
int v=e[i].to;
if(vis[v]) continue;
dfs(v),merge(u,v);
for(int i=h1[u];i;i=e1[i].nt)
int v=e1[i].to;
if(vis[v]) e1[i].lca=find(v);
int main()
scanf("%d%d%d",&n,&m,&st);
for(int i=1,u,v;i<n;i++)
scanf("%d%d",&u,&v);add(u,v);
for(int i=1,u,v;i<=m;i++)
scanf("%d%d",&u,&v),add1(u,v);
dfs(st);
for(int i=1;i<=cnt2;i+=2) //输出
printf("%d\\n",!e1[i].lca?e1[i+1].lca:e1[i].lca); //这里值得注意，可能只有正向边或者反向边lca被赋值了
return 0;
欧拉序LCA
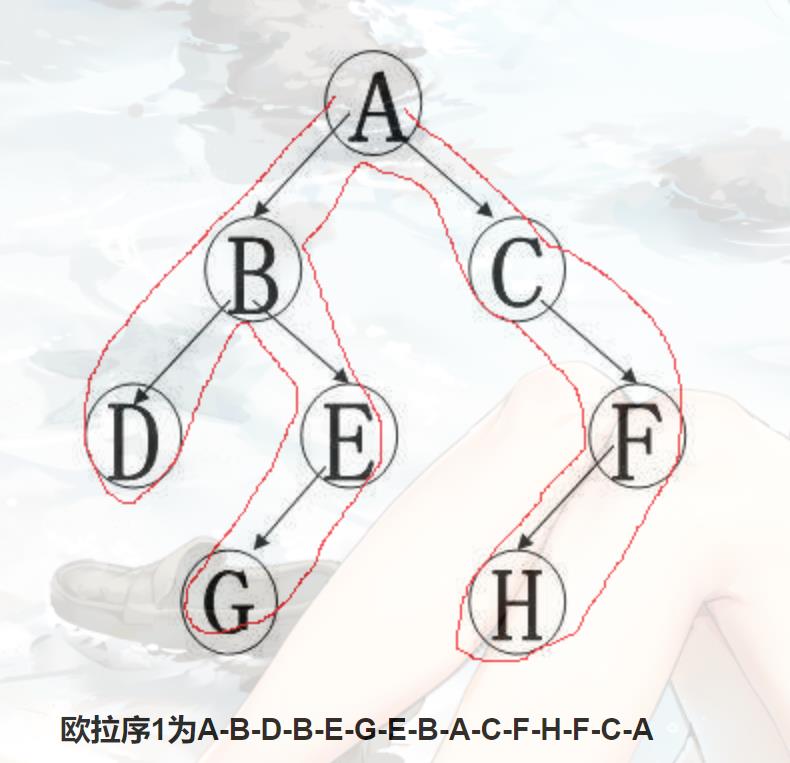
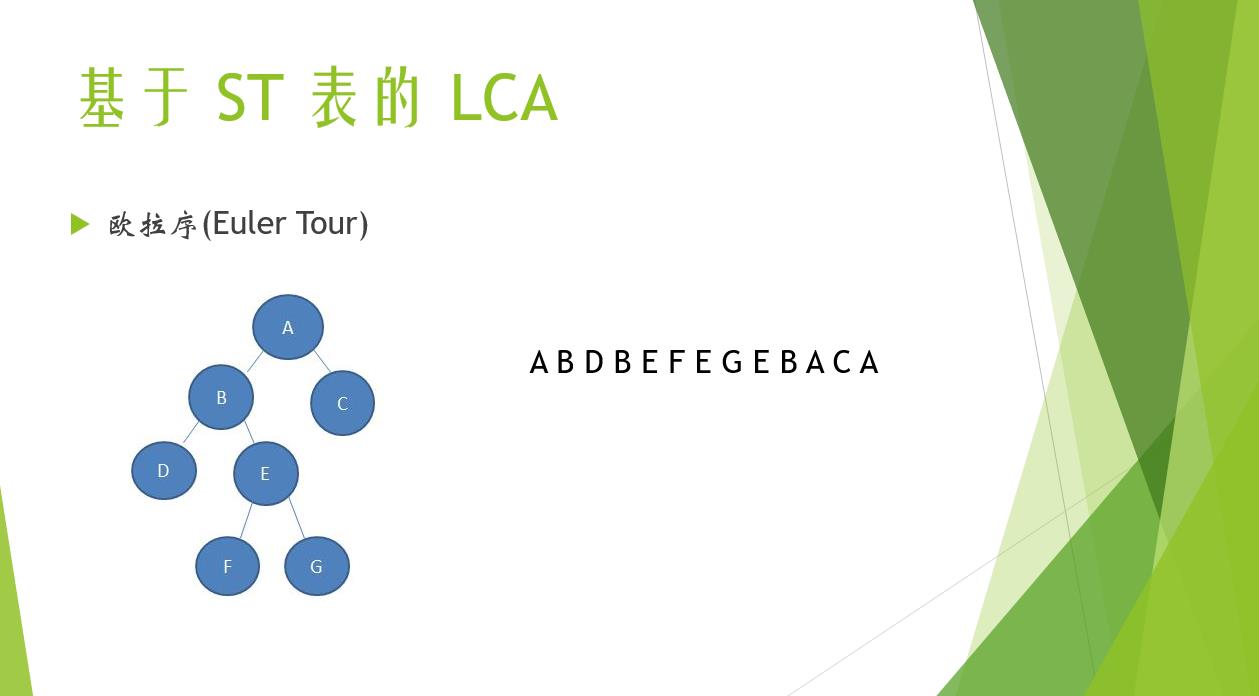
void dfs(int x,int fa)
dep[x]=dep[fa]+1,arr[++tot]=x,pos[x]=tot; //arr：欧拉序列
for(int i=hd[x];i;i=nxt[i])
int y=to[i];
if(y==fa) continue;
dfs(y,x),arr[++tot]=x;
void getst()
for(int i=1;i<=tot;i++) f[i][0]=arr[i];
for(int j=1;(1<<j)<=tot;j++)
for(int i=1;i+(1<<(j-1))<=tot;i++)
f[i][j]=(dep[f[i][j-1]]<dep[f[i+(1<<(j-1))][j-1]]?f[i][j-1]:f[i+(1<<(j-1))][j-1]);
int lca(int x,int y)
int l=pos[x],r=pos[y];
if(l>r) swap(l,r);
int k=log2(r-l+1),u=f[l][k],v=f[r-(1<<k)+1][k]; //log2 可能会被卡常
return dep[u]<dep[v]?u:v;
树剖LCA
//树剖LCA
struct edge
int to,nt;
e[N<<1];
int h[N],cnt;
void add(int u,int v)
e[++cnt]=v,h[u],h[u]=cnt;
e[++cnt]=u,h[v],h[v]=cnt;
int sz[N],fa[N],son[N],top[N],dfn[N],dep[N];
void dfs(int u,int f)
sz[u]=1,fa[u]=f,dep[u]=dep[f]+1;
for(int i=h[u];i;i=e[i].nt)
int v=e[i].to;
if(v==f) continue;
dfs(v,u);
sz[u]+=sz[v];
if(sz[son[u]]<sz[v]) son以上是关于树的直径和LCA的主要内容，如果未能解决你的问题，请参考以下文章
[51nod] 1766树上的最远点对 树的直径 树剖LCA+ST表静态查询
[51nod] 1766树上的最远点对 树的直径 树剖LCA+ST表静态查询