滑动窗口2：滑动窗口算法基本原理

Posted 2021-12-13 纵横千里，捭阖四方

学过计算机网络的同学都知道滑动窗口协议（Sliding Window Protocol），该协议是 TCP协议 的实现的核心策略之一，用于网络数据传输时的流量控制，以避免拥塞的发生。该协议允许发送方在停止并等待确认前发送多个数据分组。由于发送方不必每发一个分组就停下来等待确认。因此该协议可以加速数据的传输，提高网络吞吐量。事实上在与流量控制、熔断、限流、超时等场景下都会首先从滑动窗口的角度来思考问题，例如hystrix、sentinel等框架都使用了这种思想。

滑动窗口算法也是一种思想，是双指针的拓展和延伸，很多算法题目都可以基于该思想来解决，所以我们就将两者放在一起学习。

首先明白什么是滑动、什么是窗口：

• 滑动：说明这个窗口是移动的，也就是移动是按照一定方向来的。

• 窗口：窗口大小并不是固定的，可以不断扩容直到满足一定的条件；也可以不断缩小，直到找到一个满足条件的最小窗口；当然也可以是固定大小。

滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作。

简而言之，滑动窗口算法在一个特定大小的字符串或数组上进行操作，而不在整个字符串和数组上操作，这样就降低了问题的复杂度，从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。

假如窗口的大小是3，当不断有新数据来时，我们都会维护一个大小为3的一个范围来标记，超过3的就将新的放入，老的移走，这其实与大小固定的队列非常像。不同的是数据可能保存在一个很大的空间，我们仅仅在其上面使用两个最大距离固定的标记来标记其上面的一个区域而已。例如：

 可以用来解决一些查找满足一定条件的连续区间的性质（长度等）的问题。由于区间连续，因此当区间发生变化时，可以通过旧有的计算结果对搜索空间进行剪枝，这样便减少了重复计算，降低了时间复杂度。往往类似于“ 请找到满足 xx 的最 x 的区间（子串、子数组）的 xx ”这类问题都可以使用该方法进行解决。

为了便于理解，这里采用的是字符串来讲解。但是对于数组其实也是一样的。滑动窗口算法的思路是这样：

1. 我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。

2. 我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

3. 此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

4. 重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

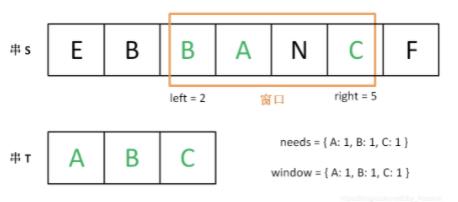
下面画图理解一下，needs 和 window 相当于计数器，分别记录 T 中字符出现次数和窗口中的相应字符的出现次数：

初始状态：

增加 right，直到窗口 [left, right] 包含了 T 中所有字符：

 

 直到窗口中的字符串不再符合要求，left 不再继续移动。

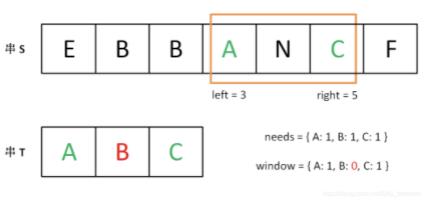
 之后重复上述过程，先移动 right，再移动 left…… 直到 right 指针到达字符串 S 的末端，算法结束。

如果你能够理解上述过程，恭喜，你已经完全掌握了滑动窗口算法思想。至于如何具体到问题，如何得出此题的答案，都是编程问题，等会提供一套模板，理解一下就会了。

上述过程对于非固定大小的滑动窗口，可以简单地写出如下基本框架：

string s, t;
    // 在 s 中寻找 t 的「最小覆盖子串」
    int left = 0, right = 0;
    string res = s;
    
    while(right < s.size()) {
        window.add(s[right]);
        right++;
        // 如果符合要求，说明窗口构造完成，移动 left 缩小窗口
        while (window 符合要求) {
            // 如果这个窗口的子串更短，则更新 res
            res = minLen(res, window);
            window.remove(s[left]);
            left++;
        }
    }
    return res;

这个与双指针基本一致，但是对于固定窗口大小k，此时不需要依赖 left 指针了，因为left = right-k可以总结如下：

// 固定窗口大小为 k
    string s;
    // 在 s 中寻找窗口大小为 k 时的所包含最大元音字母个数
    int  right = 0;while(right < s.size()) {
        window.add(s[right]);
        right++;
        // 如果符合要求，说明窗口构造完成，
        if (right>=k) {
            // 这是已经是一个窗口了，根据条件做一些事情
           // ... 可以计算窗口最大值等 
            // 最后不要忘记把 right -k 位置元素从窗口里面移除
        }
    }
    return res;

这两章，我们学习了双指针和滑动窗口的基本原理，接下来，我们就开始分析很多典型的LeetCode题目。