滑动窗口3：Leetcode 11 盛水最多的容器

Posted 2021-12-13 纵横千里，捭阖四方

题目要求：

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

示例1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

 这个题是一道经常在笔试中出现的题目，这道题的最优方法就是双指针。

我们先从题目中的示例开始，一步一步观察解决过程，我们第一感觉是找距离最远和高度最高的那些，但是这样的话两个变量同时变， 这时候就要我们将所有矩形都找到，然后分别计算面积，最好找最大。但是这样会进行大量的计算，所以不可取。

不妨我们先从距离最远的两个位置开始，题目中的示例为：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
 ^                       ^

在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 min(1, 7) * 8 = 8min(1,7)∗8=8。

此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由“两个指针指向的数字中较小值∗指针之间的距离”决定的。因此不管怎么调整，距离一定是在减小的，那我们自然调整小的更合适，如果下一个更高那就赚了，如果更小那就继续找。例如1后面的是8，显然此时就是min(8,7)*(8-1)=49。

那这时候是否可以同时移动呢？此时不管移动哪一侧，都是一个新的矩阵，所以我们可以一个个计算的。

所以，我们将左指针向右移动：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
    ^                    ^

此时可以容纳的水量为 \\min(8, 7) * 7 = 49min(8,7)∗7=49。那么接下来要移动谁呢？显然距离会继续减小的，我们移动7更可能赚，也就是从7到3，显然min(8,3)∗6=18，更小了，我们就继续将右侧从3到8，此时为min(8,8)∗5=40。两指针对应的数字相同，我们可以任意移动一个，例如如果移动左指针，那么就是min(6,8)∗4=24。

由于左指针对应的数字较小，我们移动左指针，并且可以发现，在这之后左指针对应的数字总是较小，因此我们会一直移动左指针，直到两个指针重合。在这期间，对应的可以容纳的水量为：min(2, 8) * 3 = 6min(2,8)∗3=6，min(5, 8) * 2 = 10min(5,8)∗2=10，min(4, 8) * 1 = 4min(4,8)∗1=4。

在我们移动指针的过程中，计算到的最多可以容纳的数量为 49，即为最终的答案。

不过不放心，我们再看一个更简单一点的例子：

 我们首先计算的是min(6,5)*5=25

然后计算min(6,3)*4=12

接着计算min(6,6)*3=18;

接着计算min(5,6)*2=10

最后是min(5,7)*1=5

这里可能想不明白的是，中间很多矩形我们并没有计算，例如min(5,5)*4=20,没有计算，那为什么能保证不在最大容量之内呢？其实从图里我们可以看到min(6,5)*5一定是大于min(5,5)*4的，我们采取双指针的策略就是为了减少无关计算的。

那这里为什么双指针的做法是正确的呢？

双指针代表的是 可以作为容器边界的所有位置的范围。在一开始，双指针指向数组的左右边界，表示 数组中所有的位置都可以作为容器的边界，因为我们还没有进行过任何尝试。在这之后，我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置，就表示我们认为 这个指针不可能再作为容器的边界了。

 为什么对应的数字较小的那个指针不可能再作为容器的边界了？

在上面的分析部分，我们对这个问题有了一点初步的想法。这里我们定量地进行证明。

考虑第一步，假设当前左指针和右指针指向的数分别为 x和 y，我们假设 x≤y。同时，两个指针之间的距离为 t。那么，它们组成的容器的容量为：

 

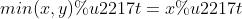
 我们可以断定，如果我们保持左指针的位置不变，那么无论右指针在哪里，这个容器的容量都不会超过 x * tx∗t 了。注意这里右指针只能向左移动，因为 我们考虑的是第一步，也就是 指针还指向数组的左右边界的时候。

我们任意向左移动右指针，指向的数为，指向的数为,两个指针之间的距离为t1，那么显然有t1<t2,并且min(x,y1)<min(x,y):

• 如果y1<=y,那么min(x,y1)<=min(x,y)
• 如果y1>y,那么min(x,y1)=x=min(x,y)

因此有：

min(x,yt)*t1<min(x,y)*t;

即无论我们怎么移动右指针，得到的容器的容量都小于移动前容器的容量。

这样以来，我们将问题的规模减小了 11，被我们丢弃的那个位置就相当于消失了。此时的左右指针，就指向了一个新的、规模减少了的问题的数组的左右边界，因此，我们可以继续像之前 考虑第一步 那样考虑这个问题：

• 求出当前双指针对应的容器的容量；
• 对应数字较小的那个指针以后不可能作为容器的边界了，将其丢弃，并移动对应的指针

所以最后的策略就是我们每次以双指针为左右边界（也就是「数组」的左右边界）计算出的容量中的最大值。

所以代码就是：

public class Solution {
    public int maxArea(int[] height) {
        int l = 0, r = height.length - 1;
        int ans = 0;
        while (l < r) {
            int area = Math.min(height[l], height[r]) * (r - l);
            ans = Math.max(ans, area);
            if (height[l] <= height[r]) {
                ++l;
            }
            else {
                --r;
            }
        }
        return ans;
    }
}