堆的问题：大堆小堆都能解决LeetCode215 在数组中找第K大的元素

Posted 2021-12-13 纵横千里，捭阖四方

LeetCode215题：给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

示例1：
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例2：
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

这个题是一道非常重要的题，主要解决方法有三个，选择法，堆排序法和快速排序法。

选择法很简单，就是先遍历一遍找到最大的元素，然后再遍历一遍找第二大的，然后再遍历一遍找第三大的，直到第K次就找到了目标值了。但是这种方法只适合在面试的时候预热，面试官不会让你这么简单就开始写代码，因此该方法的时间复杂度为O(NK)。

这道题比较好的方法是堆和快速排序法。今天我们看堆如何解决问题。首先来看，到底使用哪种堆呢？答案是大堆小堆都可以。

1.基于大顶堆来做

我们先根据之前介绍的建堆方法来建立大顶堆：

 

我们知道每次根节点都是整个堆里最大的那个，那我们每次都删除根节点然后调整，删根节点再调整，反复执行3次，那最后剩下的堆顶是不是就是要找的元素了呢？

具体步骤：

先删除6，再将剩余的元素调整为大顶堆，过程为：

 

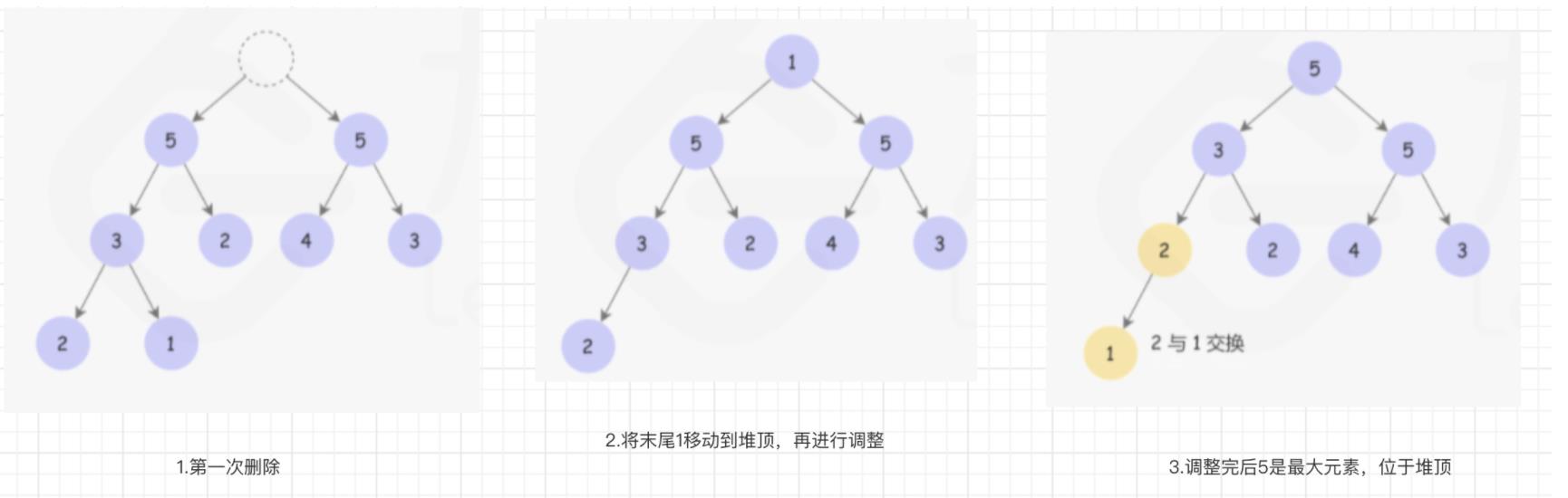
然后删除5，再进行第二次调整，依次类推。

执行3轮之后的堆结构如下有图所示。

 这时候直接返回堆的根元素4就行了， 这就是堆是如何解决找第K个问题的。

代码实现比较复杂，我们这里只是看一下就行了，

class Solution {
    public int findKthLargest(int[] nums, int k) {
        int heapSize = nums.length;
        buildMaxHeap(nums, heapSize);
        for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
            swap(nums, 0, i);
            --heapSize;
            maxHeapify(nums, 0, heapSize);
        }
        return nums[0];
    }

    public void buildMaxHeap(int[] a, int heapSize) {
        for (int i = heapSize / 2; i >= 0; --i) {
            maxHeapify(a, i, heapSize);
        } 
    }

    public void maxHeapify(int[] a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a, i, largest);
            maxHeapify(a, largest, heapSize);
        }
    }

    public void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

假如这里nums是一个很大的数据，不是小的数组，或者是流数据， 没头没尾该怎么办呢？堆还能不能解决？可以的，甚至只能用堆来解决。

2.基于小根堆来做

我们推荐使用“找大就用小堆，找小就用大堆”的策略，因为更好理解，适用题目也更多，特别是流数据和大数据的情况。而这正好对应了LeetCode703 数据流中找第K大元素的题目，我们就干脆看一下703题怎么做吧。

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

• KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。

• int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

输入：
["KthLargest", "add", "add", "add", "add", "add"]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
输出：
[null, 4, 5, 5, 8, 8]

解释：
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3);   // return 4
kthLargest.add(5);   // return 5
kthLargest.add(10);  // return 5
kthLargest.add(9);   // return 8
kthLargest.add(4);   // return 8

这个题说得很啰嗦，无非就是初始堆是4 5 8 2 四个元素，之后不断插入3 5 10 9 4 .....，每次都返回第3大的数字。

这个题几乎只能用堆来进行。同样，我们可以把流数据换成无穷大的数组，大数据等等都是一样的解法。

我们上面介绍的题中，可以先将全部元素塞到完全二叉树里，然后再逐步构造成堆，最后删掉K-1个元素就得到我们需要的了，显然对于流数据和大数据就不行了。

我们需要先构造一个元素大小为K的小根堆，新元素来的时候与根元素对比：

• 如果新元素比根元素大，则删除根结点，并将新元素入堆。

• 如果新元素比根结点小，则不做处理。

• 需要求第K大时，返回根节点就行了。

为啥要这样呢？我们画图看看：

假如原始序列为[5,6,7,8,9,10,11,12,4,3,2,1,......] ，要求第5大的元素。则我们建立一个大小为5的小根堆，然后插入10 的过程为：

 

显然，如果此时要返回第K大自然就是6了。

我们继续插入11 和12之后的结构为：

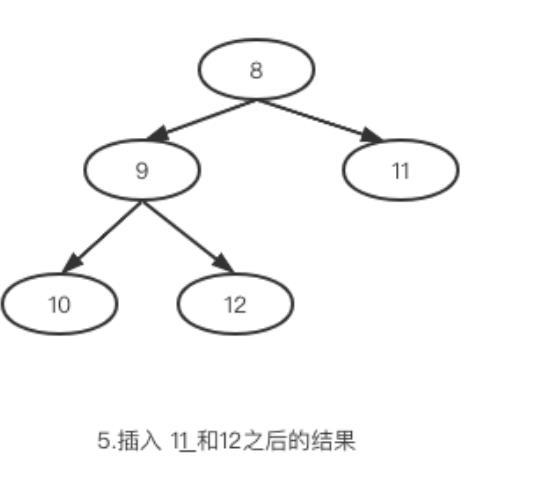
显然此时的第K大就是8。

如果继续出现 1，2，3，4 等比8小的数，因为都比8小，所以都不会入堆，所以此时第K大还是8。

由此我们看到，不管原始数据是多少，只要用小根堆走一遍就找到需要的结果了。

因此，我们的解题方法是：

我们可以使用一个大小为 k的优先队列来存储前 k 大的元素，其中优先队列的队头为队列中最小的元素，也就是第 k大的元素。

在单次插入的操作中，我们首先将元素val 加入到优先队列中。如果此时优先队列的大小大于 k，我们需要将优先队列的队头元素弹出，以保证优先队列的大小为 k。

代码如下：

class KthLargest {
    PriorityQueue<Integer> pq;
    int k;

    public KthLargest(int k, int[] nums) {
        this.k = k;
        pq = new PriorityQueue<Integer>();
        for (int x : nums) {
            add(x);
        }
    }
    
    public int add(int val) {
        pq.offer(val);
        if (pq.size() > k) {
            pq.poll();
        }
        return pq.peek();
    }
}

 反过来，如果找第K小呢？就要用大根堆了。

所以我们说：找第K大用小根堆，找第K小用大根堆。