恒源云_基于梯度的NLP对抗攻击方法

Posted 2021-12-13 AI酱油君

文章来源 | 恒源云社区（专注人工智能/深度学习云GPU服务器训练平台，官方体验网址：gpushare.com/ ）

原文地址 | https://bbs.gpushare.com/topic/707/%E5%9F%BA%E4%BA%8E%E6%A2%AF%E5%BA%A6%E7%9A%84nlp%E5%AF%B9%E6%8A%97%E6%94%BB%E5%87%BB%E6%96%B9%E6%B3%95?_=1637048101498

原文作者 | Mathor

---

前言：
Facebook提出了一种NLP通用的攻击方法，而且可以通过梯度优化，论文发表在EMNLP2021，名为Gradient-based Adversarial Attacks against Text Transformers，源码在facebookresearch/text-adversarial-attack

BACKGROUND

我们首先定义模型$h:\mathcal{X}$ $\to \mathcal{Y}$，其中$\mathcal{X}$和$\mathcal{Y}$分别是输入输出集。设测试样本$x\in \mathcal{X}$被模型正确预测为标签$y$，则有$y=h(x)\in \mathcal{Y}$。如果一个与$x$无限接近的对抗样本${\mathbf{x}}^{\prime }$使得$h({\mathbf{x}}^{\prime })\ne y$，则${\mathbf{x}}^{\prime }$是一个好的对抗样本。我们可以通过定义函数$\rho :\mathcal{X}\times \mathcal{X}\to {\mathbb{R}}_{\ge 0}$ 来量化$\mathbf{x}$和${\mathbf{x}}^{\prime }$的接近程度。设阈值$ϵ>0$，如果 $\rho (\mathbf{x},{\mathbf{x}}^{\prime })\le ϵ$，则认为对抗样本${\mathbf{x}}^{\prime }$与样本$\mathbf{x}$非常接近

寻找对抗样本的过程通过被视为一个优化问题，例如对于分类问题来说，模型$h$输出一个logits向量${\varphi }_h(\mathbf{x})\in {\mathbb{R}}^K$，使得$y=\arg ma{x}_k{\varphi }_h(\mathbf{x}{)}_k$ ，为了使得模型预测错误，我们可以将margin loss选作对抗损失：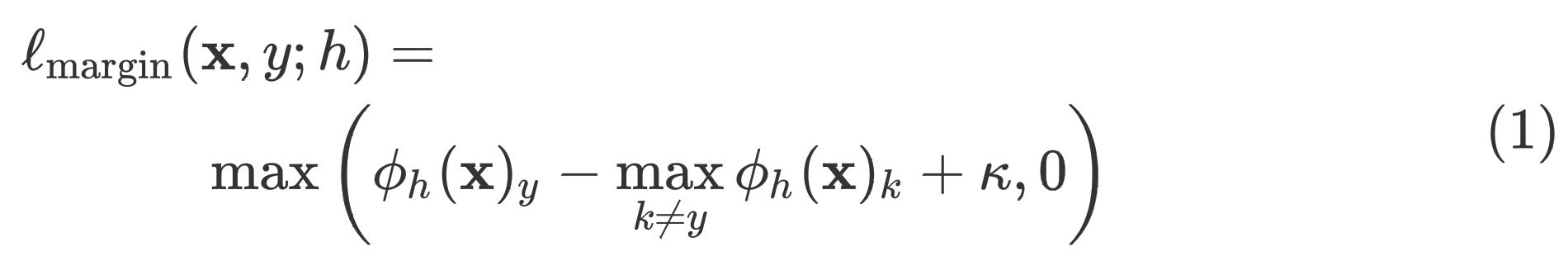

当损失为0的时候，模型会在超参数$\kappa$的控制下预测错误。margin loss在2017年的论文Towards evaluating the robustness of neural networks，关于图像对抗算法中就被证明过有效

这部分注释我想仔细解释下为什么margin loss可以使得模型分类错误。模型训练的最终目的是为了优化margin loss，使得它的损失值降为0，即

只要满足上式情况，损失值就为0了。通过变形我们可以得到

其中，${\varphi }_h(\mathbf{x}{)}_y$指的是输入$\mathbf{x}$被模型正确预测为类别$y$的logit值。不妨设

并且$i\ne y$，这表明在所有的错误类别中，第$i$类的logit最大，并且结合上面的不等式可得

总结一下，我们的优化目标永远都是使得损失值降为0，但是损失降为0并不一定代表就要模型对所有的样本都正确预测，margin loss优化的目标就是使得模型预测错误类别$i$的logit比预测正确类别$y$的logit大$\kappa$。但凡存在一个样本预测正确，损失都不可能为0

给定对抗损失$\ell$，构造对抗样本的过程可以被视为一个有限制的优化问题：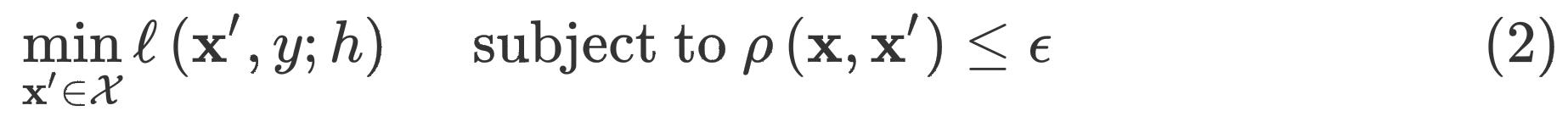

我们可以把约束$\rho$带入损失函数中，将原本的硬约束变为软约束

如果约束函数$\rho$是可微的，就可以用基于梯度的优化器来优化了

式(2)在图像或者语音等连续数据领域已被广泛应用，但实际上它并不适用于文本数据，主要有两点原因：

1. 数据空间$\mathcal{X}$是离散的，因此无法利用梯度进行优化
2. 约束函数$\rho$难以度量文本数据，例如在一个句子中插入"不是"，这个词会否定整个句子的意义，但如果我们用编辑距离去计算两个句子的差异，它们的编辑距离仅为1

GBDA: GRADIENT-BASED DISTRIBUTIONAL ATTACK

论文作者所提出的方法解决了上面两个问题：

1. 利用**Gumbel-Softmax**使得采样过程可以被梯度优化
2. 通过引入困惑度和语义相似度这两个软约束，促使对抗样本的语义更加流畅以及与原样本间的语义更接近

Adversarial Distribution
令$\mathbf{z}=z_1{z}_2\cdots z_n$是句子$\mathbf{z}$的token序列，其中$z_i$ 来自于一个固定的词汇表$\mathcal{V}=1,\dots ,V$。设概率分布$P_{\Theta }$来自于一个参数化的概率矩阵$\Theta \in {\mathbb{R}}^{n\times V}$，句子$z\sim P\Theta$中的每个token都是通过下面的公式独立抽样出来的

其中，${\pi }_i=\text{Softmax}({\Theta }_i)$表示第$i$个token概率分布的向量

我们的目标是优化参数矩阵$\Theta$，使得$\mathbf{z}\sim P_{\Theta }$ 为模型$h$的对抗样本，为了做到这一点，我们需要优化的目标函数为

其中，$\ell$为可选的对抗损失，例如margin loss

Extension to probability vector inputs
公式(5)很明显不是一个可导的函数，因为分布是离散的，并且我们是通过采样得到的，采样这个操作没有公式，也就无法求导。但是，我们可以对公式(5)进行缩放，将概率向量作为输入，并且使用Gumbel-Softamx作为$\arg \max$的估计值，以此来引入梯度

句子$\mathbf{z}$中每个token $z_i$ 在Vocabulary中的索引$i$可以通过Word Embedding表查到相应的词向量。特别地，我们定义$\mathbf{e}(\cdot )$为embedding函数，因此token $z_i$ 的embedding为$\mathbf{e}(z_i)\in {\mathbb{R}}^{d}e$，其中$d$是embedding维度。给定一个概率向量${\pi }_i$ ，它决定了token$z_i$ 的抽样概率，则我们定义

为对应于概率向量${\pi }_i$的嵌入向量。特别地，如果token $z_i$的概率向量${\pi }_i$是一个one-hot向量，则$\mathbf{e}({\pi }_i)=\mathbf{e}(z_i)$。有了公式(6)，我们可以将输入概率向量序列 π = π 1 ⋯ π n \\boldsymbol{\\pi} = \\pi_1\\cdots \\pi_n π=π1​⋯π<

以上是关于恒源云_基于梯度的NLP对抗攻击方法的主要内容，如果未能解决你的问题，请参考以下文章

图像对抗算法-攻击篇（I-FGSM）

图像对抗算法-攻击篇（FGSM）

华为开源自研AI框架昇思MindSpore应用实践：FGSM网络对抗攻击

繁凡的对抗攻击论文精读CVPR 2019 基于决策的高效人脸识别黑盒对抗攻击（清华朱军）

ML对抗攻击

20155333 《网络对抗》 Exp5 MSF基础应用