C Language 二叉树 - 二叉树的遍历（十四）

Posted 2021-12-13 Adorable_Rocy

二叉树遍历有多种方式，先序、中序、后序、层次遍历四种遍历方式，下面一起来看看吧

补充：关于四种遍历方式已经在上一篇文章中给出：Tree和BinaryTree（十三）

---

1.二叉树的递归遍历算法

先：ABDHEFCGI
中：HDBEFACIG
后：HDFEBIGCA

有二叉树如下：
A(B(D(H),E(,F)),C(,G(I))

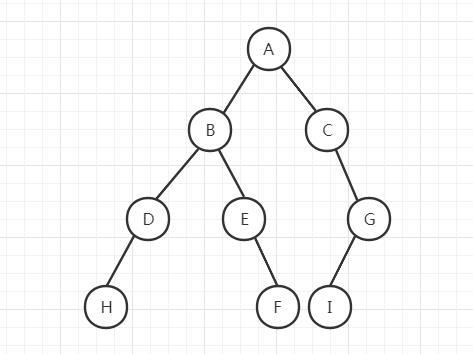
1.先序遍历

//先序输出
void PreOrder(BTNode *bnode){
	if(bnode!=NULL){
		printf("%3c",bnode->data);
		PreOrder(bnode->lchild);
		PreOrder(bnode->rchild);
	}
} 

2.中序遍历

//中序输出
void InOrder(BTNode *bnode){
	if(bnode!=NULL){
		InOrder(bnode->lchild);
			printf("%3c",bnode->data);
		InOrder(bnode->rchild);
	}
} 

3.后序遍历

//后序输出
void PostOrder(BTNode *bnode){
	if(bnode!=NULL){
		PostOrder(bnode->lchild);
		PostOrder(bnode->rchild);
			printf("%3c",bnode->data);
	}
} 

输出结果如下：

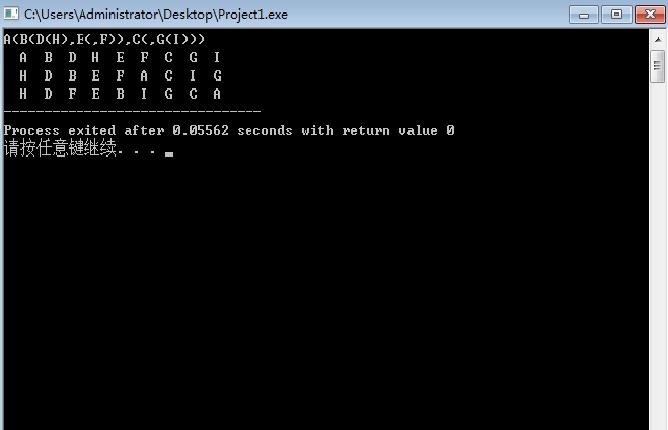
2.二叉树的非递归算法

前言：关于二叉树的非递归算法，可以采用栈的运算算法进行设计，先进栈的后出栈的原则，进行算法的设计。

1.先序遍历

//非递归的先序算法 
void SqStackPreOrder(BTNode *bnode) {
	BTNode *b;
	SqStack *st;
	initStack(st);  //初始化栈
	if(bnode != NULL) {
		Push(st,bnode);   	   //进栈操作
		while(!StackEmpty(st)) {  //栈不为空时循环
			Pop(st,b);  	 //退栈
			printf("%3c",b->data);	//输出元素
			if(b->rchild != NULL) {			//先进后出 先序是DLR 所以先进R然后出R 
				Push(st,b->rchild);
			} 
			if(b->lchild != NULL){
				Push(st,b->lchild);
			}
		}
	}
}

2.中序遍历

//中序非递归算法 
void SqStackInOrder(BTNode *bnode) {
	BTNode *b;
	SqStack *st;
	initStack(st);  //初始化栈
	b = bnode;
	while(!StackEmpty(st)|| b != NULL) {
		while(b != NULL) {  //扫描所有的左子树并且一一添加 
				Push(st,b);
				b = b->lchild;  //一直添加 
		}
		
		//右子树的左子树  到最左下角 然后出栈最左下角的元素 再添加右子树的结点 
		//如果右子树没有左子树了 就继续出栈 
		if(!StackEmpty(st)){
			Pop(st,b); 			//出栈元素
			printf("%3c",b->data);
			b = b->rchild; 
		}
	}
	printf("\\n"); 
}

3.后续遍历

//后序遍历的非递归算法
void SqStackPostOrder(BTNode *bnode){
	BTNode *b , *r;
	bool flag;
	SqStack *st;
	initStack(st);
	b = bnode;
	do{
		while(b != NULL){		//顺序入栈 左子树进栈 
			Push(st,b);
			b = b->lchild;	
		}
		r = NULL;				//初始化指针r 
		flag = true;     		//表示正在处理的栈顶结点
		while(!StackEmpty(st) && flag){
			GetTop(st,b);			//取出栈顶结点p 
			if(b->rchild == r){ 	//如果结点为空或者为刚访问过的结点 
				printf("%3c",b->data);
				Pop(st,b);
				r = b;		//r指向之前访问过的结点 
			}else{
				b = b->rchild;
				flag = false;
			}
		} 
	}while(!StackEmpty(st));
	printf("\\n");
}

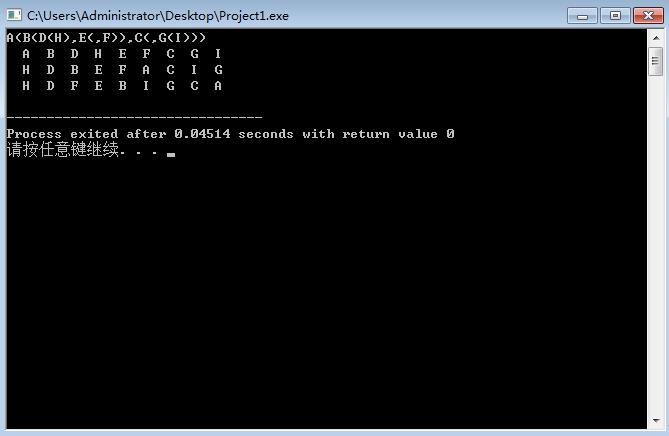
• 附赠：完整代码如下：

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#define MaxSons 5
#define MaxSize 20

typedef struct SqNode {
	char data;
	struct SqNode *lchild;
	struct SqNode *rchild;
} BTNode;

//创建栈
typedef struct {
	BTNode *data[MaxSize];
	int top;
} SqStack;

//创建二叉树
void createBiTree(BTNode *&node , char *str) {

	BTNode *St[MaxSize] , *p; //创建顺序栈
	int top = -1,k,j = 0; //栈顶指针以及str数组指针
	char ch ;
	node = NULL;
	ch = str[j];
	while(ch != '\\0') { //循环遍历str数值
		switch(ch) {
			case '(':
				top++;
				St[top] = p;
				k=1;
				break;
			case ')':
				top--;
				break;
			case ',':
				k=2;
				break;
			default:
				p = (BTNode *)malloc(sizeof(BTNode));
				p->data = ch;
				p->lchild = p->rchild = NULL;
				if(node == NULL) {
					node = p;
				} else {
					switch(k) {
						case 1:
							St[top]->lchild = p;
							break;
						case 2:
							St[top]->rchild = p;
							break;
					}
				}
		}
		j++;
		ch = str[j];
	}
}
//输出二叉树
void dispBtree(BTNode *b) {
	if(b!=NULL) {
		printf("%c",b->data);
		if(b->lchild != NULL || b->rchild != NULL) {
			printf("(");
			dispBtree(b->lchild);
			if(b->rchild != NULL) printf(",");
			dispBtree(b->rchild);
			printf(")");
		}
	}
}
//销毁二叉树
void  destoryBTree(BTNode *&bnode) {
	if(bnode != NULL) {
		destoryBTree(bnode->lchild);
		destoryBTree(bnode->rchild);
		free(bnode);
	}
}
//查找结点算法
BTNode *findNode(BTNode *bnode , char ch) {
	BTNode *p;
	if(bnode == NULL) {
		//没有返回值了
		return NULL;
	} else if(bnode->data == ch) {
		return bnode;
	} else {
		p = findNode(bnode->lchild,ch);
		if(p != NULL) {
			return p;
		} else {
			return findNode(bnode->rchild,ch);
		}
	}
}

//先序输出
void PreOrder(BTNode *bnode) {
	if(bnode!=NULL) {
		printf("%3c",bnode->data);
		PreOrder(bnode->lchild);
		PreOrder(bnode->rchild);
	}
}
//中序输出
void InOrder(BTNode *bnode) {
	if(bnode!=NULL) {
		InOrder(bnode->lchild);
		printf("%3c",bnode->data);
		InOrder(bnode->rchild);
	}
}
//后序输出
void PostOrder(BTNode *bnode) {
	if(bnode!=NULL) {
		PostOrder(bnode->lchild);
		PostOrder(bnode->rchild);
		printf("%3c",bnode->data);
	}
}

//初始化栈
void initStack(SqStack *&st) {
	st = (SqStack *)malloc(sizeof(SqStack));
	st->top = -1;
}

//判断栈是否为空栈
int StackEmpty(SqStack *st){
	return st->top == -1 ? 1 : 0;
} 
//获取栈顶元素
BTNode *GetTop(SqStack *st , BTNode *&b){
	if(StackEmpty(st)){
		return NULL;
	}
	b = st->data[st->top];
	return b;
} 
//进栈操作
void Push(SqStack *&st , BTNode *bnode){
	st->top = st->top + 1; 
	st->data[st->top] = bnode;
} 


//出栈
BTNode Pop(SqStack *st , BTNode *&b){
	b = st->data[st->top];
	st->top = st->top - 1;
	return *b; 
} 

//非递归的先序算法 
void SqStackPreOrder(BTNode *bnode) {
	BTNode *b;
	SqStack *st;
	initStack(st);  //初始化栈
	if(bnode != NULL) {
		Push(st,bnode);   	   //进栈操作
		while(!StackEmpty(st)) {  //栈不为空时循环
			Pop(st,b);  	 //退栈
			printf("%3c",b->data);	//输出元素
			if(b->rchild != NULL) {			//先进后出 先序是DLR 所以先进R然后出R 
				Push(st,b->rchild);
			} 
			if(b->lchild != NULL){
				Push(st,b->lchild);
			}
		}
	}
}

//中序非递归算法 
void SqStackInOrder(BTNode *bnode) {
	BTNode *b;
	SqStack *st;
	initStack(st);  //初始化栈
	b = bnode;
	while(!StackEmpty(st)|| b != NULL) {
		while(b != NULL) {  //扫描所有的左子树并且一一添加 
				Push(st,b);
				b = b->lchild;  //一直添加 
		}
		
		//右子树的左子树  到最左下角 然后出栈最左下角的元素 再添加右子树的结点 
		//如果右子树没有左子树了 就继续出栈 
		if(!StackEmpty(st)){
			Pop(st,b); 			//出栈元素
			printf("%3c",b->data);
			b = b->rchild; 
		}
	}
	printf("\\n"); 
}
//后序遍历的非递归算法
void SqStackPostOrder(BTNode *bnode){
	BTNode *b , *r;
	bool flag;
	SqStack *st;
	initStack(st);
	b = bnode;
	do{
		while(b != NULL){		//顺序入栈 左子树进栈 
			Push(st,b);
			b = b->lchild;	
		}
		r = NULL;	//初始化指针r 
		flag = true;
		while(!StackEmpty(st) && flag){
			GetTop(st,b);			//取出栈顶结点p 
			if(b->rchild == r){ 	//如果结点为空或者为刚访问过的结点 
				printf("%3c",b->data);
				Pop(st,b);
				r = b;		//r指向之前访问过的结点 
			}else{
				b = b->rchild;
				flag = false;
			}
		} 
	}while(!StackEmpty(st));
	printf("\\n");
}

main() {
	BTNode *bnode , *p;
	char *str = "A(B(D(H),E(,F)),C(,G(I))";
	createBiTree(bnode,str);
	dispBtree(bnode);
	printf("\\n");
	SqStackPreOrder(bnode);
	printf("\\n");
	SqStackInOrder(bnode);
	SqStackPostOrder(bnode);

	return 0;
}