电力负荷预测基于matlab遗传算法优化BP神经网络电力负荷预测含Matlab源码 1524期

Posted 2021-12-12 紫极神光

一、遗传算法简介

1 引言


2 遗传算法理论
2.1 遗传算法的生物学基础


2.2 遗传算法的理论基础




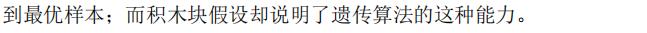
2.3 遗传算法的基本概念






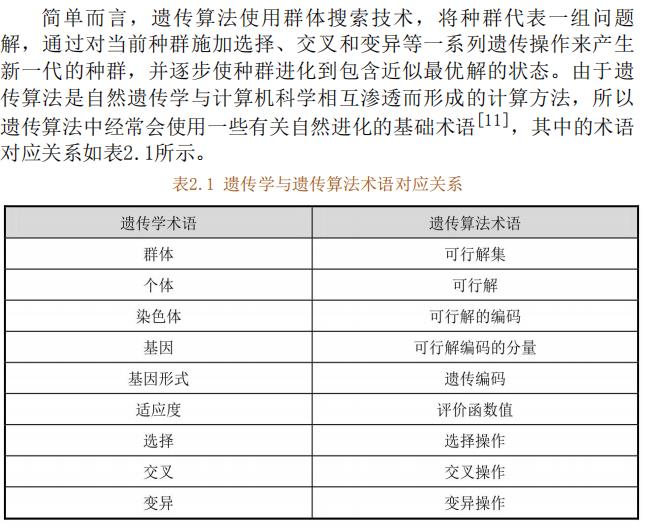
2.4 标准的遗传算法


2.5 遗传算法的特点


2.6 遗传算法的改进方向

3 遗传算法流程



4 关键参数说明

二、BP神经网络简介

1 BP神经网络预测原理简介
BP 神经网络是一种多层前馈神经网络，常用的为输入层-单隐含层-输出层的三层结构，如下图所示。

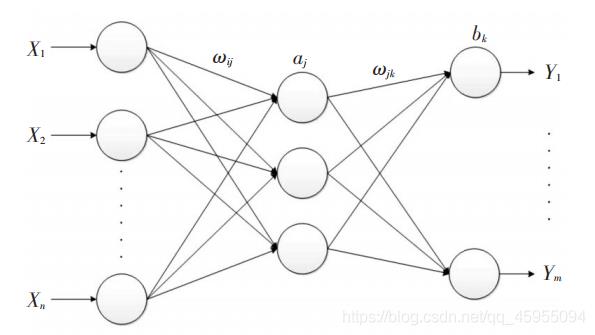
BP神经网络训练的主要思想：输入的信号特征数据先映射到隐含层（激活函数实现），再映射到输出层（默认采用线性传递函数），得到期望输出值。将期望输出值和实际测量值做比较，计算误差函数J，再将误差反向传播，通过梯度下降等算法来调节BP网络的权值和阈值。重复该过程，直到满足设定的目标误差或者最大迭代次数等终止准则，停止训练。

通过下面的例子来理解每一层的作用。

1）输入层：相当于人的五官，五官获取外部信息，对应神经网络模型input端口接收输入数据的过程。
2）隐含层：对应人的大脑，大脑对五官传递来的数据进行分析和思考，神经网络的隐含层hidden Layer对输入层传来的数据x进行映射，简单理解为一个公式hiddenLayer_output=F(w*x+b)。其中，w、b叫做权重、阈值参数，F()为映射规则，也叫激活函数，hiddenLayer_output是隐含层对于传来的数据映射的输出值。换句话说，隐含层对于输入的影响因素数据x进行了映射，产生了映射值。
3）输出层：可以对应为人的四肢，大脑对五官传来的信息经过思考（隐含层映射）之后，再控制四肢执行动作（向外部作出响应）。类似地，BP神经网络的输出层对hiddenLayer_output再次进行映射，outputLayer_output=w *hiddenLayer_output+b。其中，w、b为权重、阈值参数，outputLayer_output是神经网络输出层的输出值（也叫仿真值、预测值）（理解为，人脑对外的执行动作，比如婴儿拍打桌子）。
4）梯度下降算法：通过计算outputLayer_output和神经网络模型传入的y值之间的偏差，使用算法来相应调整权重和阈值等参数。这个过程，可以理解为婴儿拍打桌子，打偏了，根据偏离的距离远近，来调整身体使得再次挥动的胳膊不断靠近桌子，最终打中。

BP神经网络所实现的功能作用

“能尽数天星，便能尽知棋势”。围棋体现着大自然的道法，而在AlphaGo击败人类围棋冠军，则是使用算法来寻求围棋的道，实现人机对战。BP神经网络训练的结果：得到多维数据x与y之间存在的规律，即实现由x来映射逼近y。而BP训练出来得到的模型是否可靠，表现为对其他未经过训练的数据，输入到BP中，是否能输出较为准确的预测值。对此，在BP神经网络训练之后，还需要再给指标因素x1到训练好的bp network中，得到相应的BP输出值（预测值）predict1，通过作图等，计算Mse，Mape，R方等指标，来对比predict1和y1的接近程度，就可以知道模型是否预测准确。这是BP模型的测试过程，即预测过程。

小结 BP神经网络实现了：a). 根据训练集数据，训练得到一个模型，b). 对模型的可靠性与准确性进行测试集（不同于训练样本数据）预测，和实际值对比，检验预测的精度。c). 只给输入，得到预测值（可理解为测试集的数据丢了实测值，本质一样，给输入到BP中，得到输出）。由于该情况无输出，纯预测，无法检验精度是否合格，写论文时无太大意义而不必实现该情况的步骤。

2 遗传算法GA优化BP神经网络原理

在BP神经网络训练的过程中，通过前向传播数据与误差反向传递，使用算法来更新权重阈值。一方面，在该过程中，第一次前向传播过程的权重和阈值该如何确定，即如何初始化权重和阈值。深度学习的方法是采用随机化方法得到初始的权值与阈值参数。另一方面，选定了初始参数后，梯度下降算法将初始参数值作为起点，进行参数优化与更新。

在优化算法的发展中，有两类：确定性算法与启发式算法。确定性算法指使用数学方法求最优问题，找到的结果与求导的初始点有关，一般为确定值。启发式算法则是灵感源于自然界生物进化的规律，主要思想为迭代逼近最优，优化的结果为满足工程精度要求的可变值（无限接近理论最优值）。

在上述过程中，作为一种确定性算法，梯度下降算法的收敛性是得到了证明的，但收敛值并非一定是全局最优，与初始的参数值（梯度下降算法的起点）有关。由于随机初始的参数未必是最优的起点（指既训练准确，又预测可靠），因此训练的模型可靠性和稳定性受到了初始随机参数的很大影响。作为启发式算法，遗传算法GA具体很好的全局搜索能力，引入GA用来解决此问题。

主要思想 将参数作为问题的决策变量，模型的精度作为问题的目标函数。遗传算法GA优化BP神经网络的算法流程图如下：

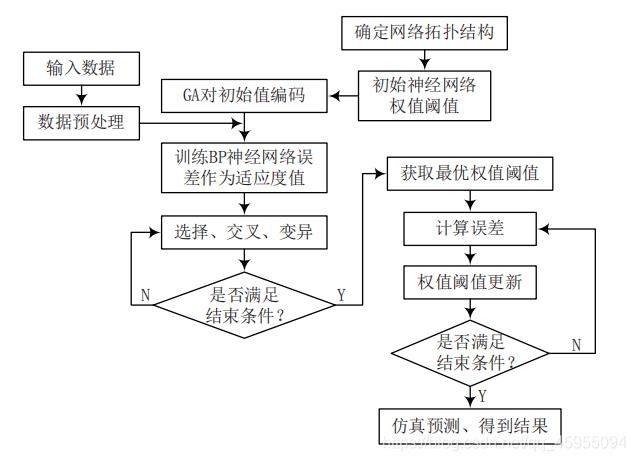
3 GA-BP模型建立
3.1 模型与数据介绍
下面以MATLAB官方提供的化学传感器的数据集为例，进行建模。
数据介绍：采集某个化学实验过程的数据，将8个传感器的采样数据作为输入（x），第9个传感器的采样数据作为输出（y）。
数据格式如下：

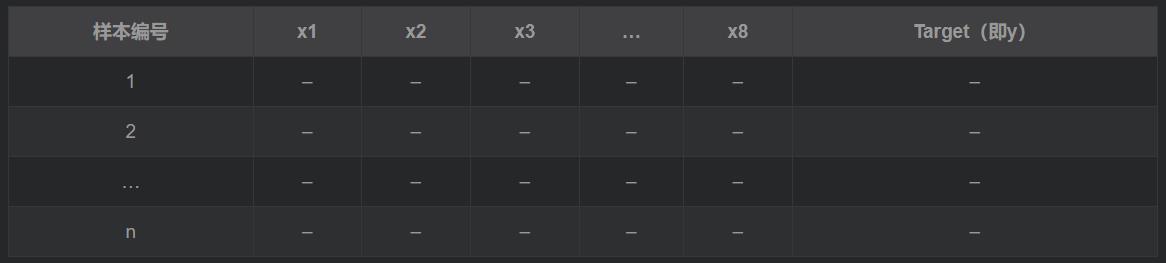
读取数据：

%% 读取读取
data=xlsread('数据.xlsx','Sheet1','A1:I498'); %%使用xlsread函数读取EXCEL中对应范围的数据即可  

%输入输出数据
input=data(:,1:end-1);    %data的第一列-倒数第二列为特征指标
output=data(:,end);  %data的最后面一列为输出的指标值

N=length(output);   %全部样本数目
testNum=100;   %设定测试样本数目
trainNum=N-testNum;    %计算训练样本数目

3.2 GA与BP参数设置
1） BP参数设置

对权重和阈值有关的参数进行说明：
a). 输入层和输出层节点使用size函数直接获取。函数用法：[M,N]=size(A)，M为A的行数，N为A的列数。size(A,2)得到的是第二个参数N，即列数。此数据中，输入8个维度指标，输出的为1个维度指标。即输入层节点为8，输出层节点为1。

inputnum=size(input,2);   %输入层神经元节点个数
outputnum=size(output,2);  %输出层神经元节点个数

b). 隐含层节点的确定过程，使用循环来遍历范围内的隐含层节点与训练误差情况。因为要找最小的误差，所以初始化训练误差时，将MSE设置较大的数字，用于在循环中确定最佳的隐含层节点。

%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a，m为输入层节点个数，n为输出层节点个数，a一般取为1-10之间的整数
MSE=1e+5; %初始化最小误差
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10

c). 其他BP参数，学习速率，训练次数，训练的目标误差等

% 网络参数
    net.trainParam.epochs=1000;         % 训练次数
    net.trainParam.lr=0.01;             % 学习速率
    net.trainParam.goal=0.000001;       % 训练目标最小误差

2）遗传算法GA参数设置

%初始化ga参数
PopulationSize_Data=30;   %初始种群规模
MaxGenerations_Data=50;   %最大进化代数
CrossoverFraction_Data=0.8;  %交叉概率
MigrationFraction_Data=0.2;   %变异概率

3.3 遗传算法优化BP的设计
1）优化变量的设计
使用遗传算法求解优化问题时，对于决策变量（优化变量）有三种编码方式：二进制编码，向量形式编码，矩阵形式编码。

由于权重和阈值分别以m×n维的矩阵，向量形式存在与BP神经网络结构（net）中。为方便对每个元素都进行优化，先将元素分别取出，然后按取的顺序放入到向量（染色体）中，完成编码。权重和阈值的经验范围为[-1,1]，可适当将寻优的范围放宽，取[-3,3]。
优化变量（元素）个数的计算如下：

nvars=inputnum*hiddennum_best+hiddennum_best+hiddennum_best*outputnum+outputnum;    %变量维度
lb=repmat(-3,nvars,1);    %自变量下限 %repmat得到一个nvars×1维的向量，每个元素的值都为-3，即优化变量下限
ub=repmat(3,nvars,1);   %自变量上限

2）适应度函数的设计
采用以下公式计算适应度值。

式中，TraingingSet，TestingSet，分别为训练集和测试集的样本。因为预测精度越高，说明误差越低，所以公式设计为求解最小的均方误差。使用遗传算法后，适应度函数值越小，表明训练越准确，且兼顾模型的预测精度更好。
3）算法设计
将遗传算法视为一个“黑箱”优化器。在确定了优化的变量与目标适应度函数后，只需要经过该“黑箱”，即可输出最小的误差（精度最好值）和最优解变量，再把变量赋给BP神经网络的权值矩阵与阈值向量的相应位置，进行优化后的BP训练与测试即可。说明：在遗传算法的“黑箱”求解器中进行的算法操作为：选择、交叉与变异。

二、部分源代码

%%% 清空环境变量
clc
clear all
close all

%%% 设置全局变量
global net inputn outputn inputps outputps output_test input_test;
global inputnum outputnum hiddennum;


%1.3 读取数据格式三：2个输入变量，2个输出变量
TrainData = textread('nanjingxunlian.txt');
TestData = textread('nanjingceshi.txt');



%1.5 训练样本输入、输出数据归一化
[inputn,inputps]=mapminmax(input_train);%inputn,inputps分别是归一化后的数据和结构体(包含最大值最小值平均数等)
[outputn,outputps]=mapminmax(output_train);

%1.6 BP网络结构
inputnum=5;   
hiddennum=3; 
outputnum=1;  

%%% 第二步： BP网络算法及其均方误差
tBP=cputime;%计时开始
[BPoutput,BPerror,BPmse,BPmape]=BP_ZHY(input_train,output_train,input_test,output_test);
eBP=cputime-tBP;%计时结束，得到建模仿真时间

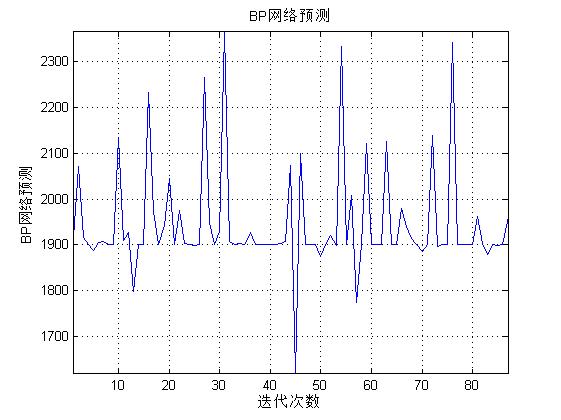
figure(3)
[r c]=size(BPoutput);
plot([1:c],BPoutput(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('BP网络预测');
title(['BP网络预测']);

figure(4)
[r c]=size(BPerror);
plot([1:c],BPerror(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('BP网络预测误差');
title(['BP网络预测误差曲线']);



%3.2 遗传算法及其最优个体
[bestchrom,trace] = GABPbestchrom_ZHY(maxgen,sizepop,pcross,pmutation);

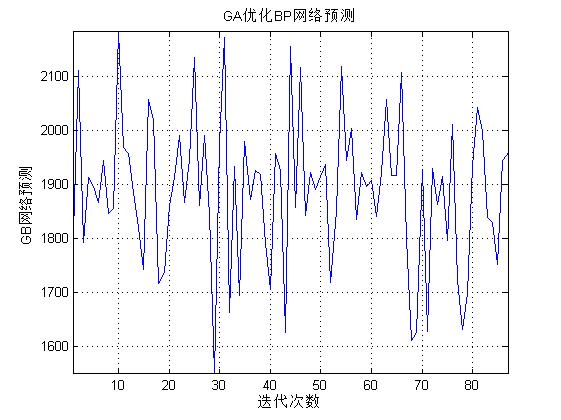
figure(5)
[r c]=size(GB_sim);
plot([1:c],GB_sim(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('GB网络预测');
title(['GA优化BP网络预测']);

figure(6)
[r c]=size(GBerror);
plot([1:c],GBerror(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('GB网络预测误差');
title(['GA优化BP网络预测误差曲线']);

%%% 第四步：两种算法结果对比分析 
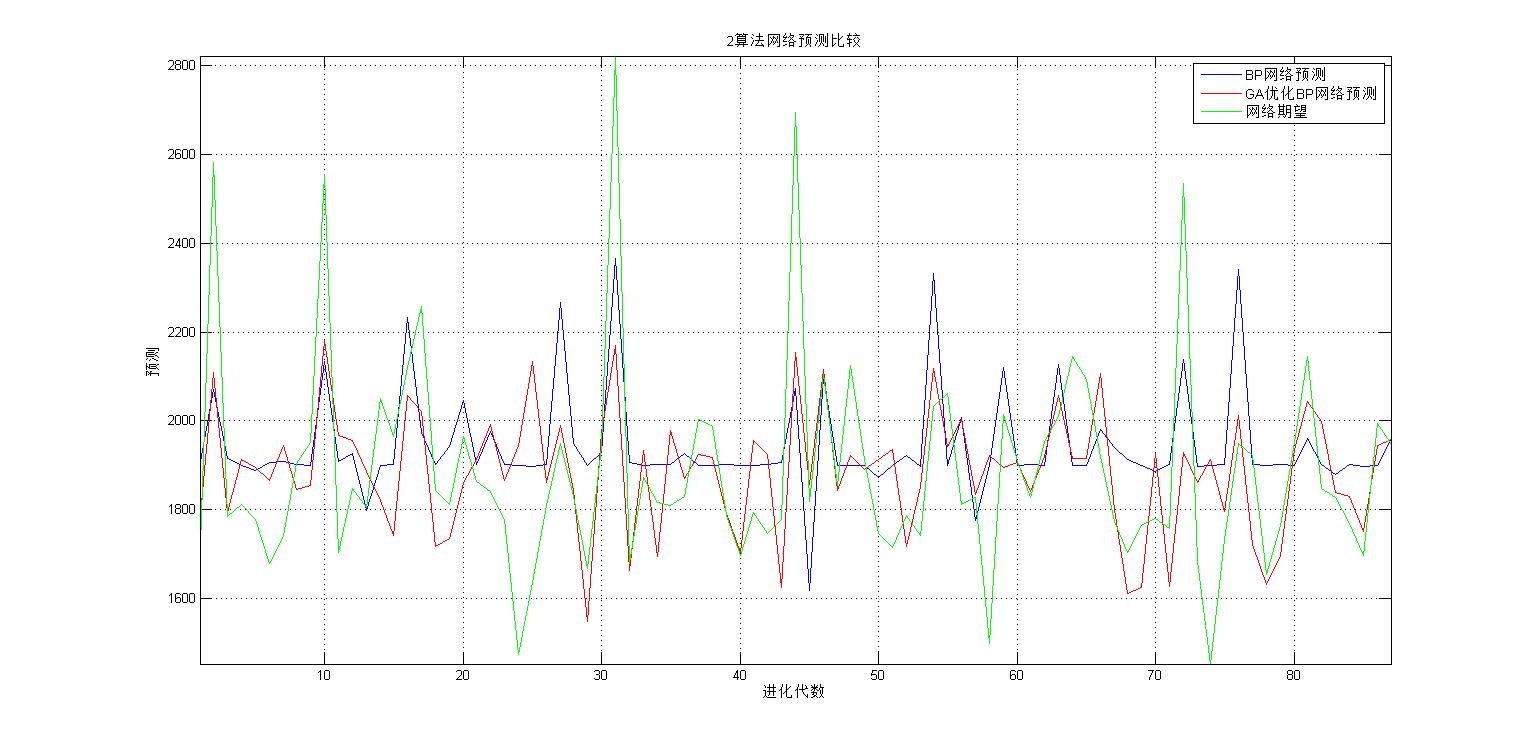
figure(7)
[r c]=size(BPerror);
plot([1:c],BPoutput(1,:),'b-',[1:c],GB_sim(1,:),'r-',[1:c],output_test(1,:),'g-');
grid;
axis tight;
xlabel('进化代数');ylabel('预测');
legend('BP网络预测','GA优化BP网络预测','网络期望');
title(['2算法网络预测比较']);

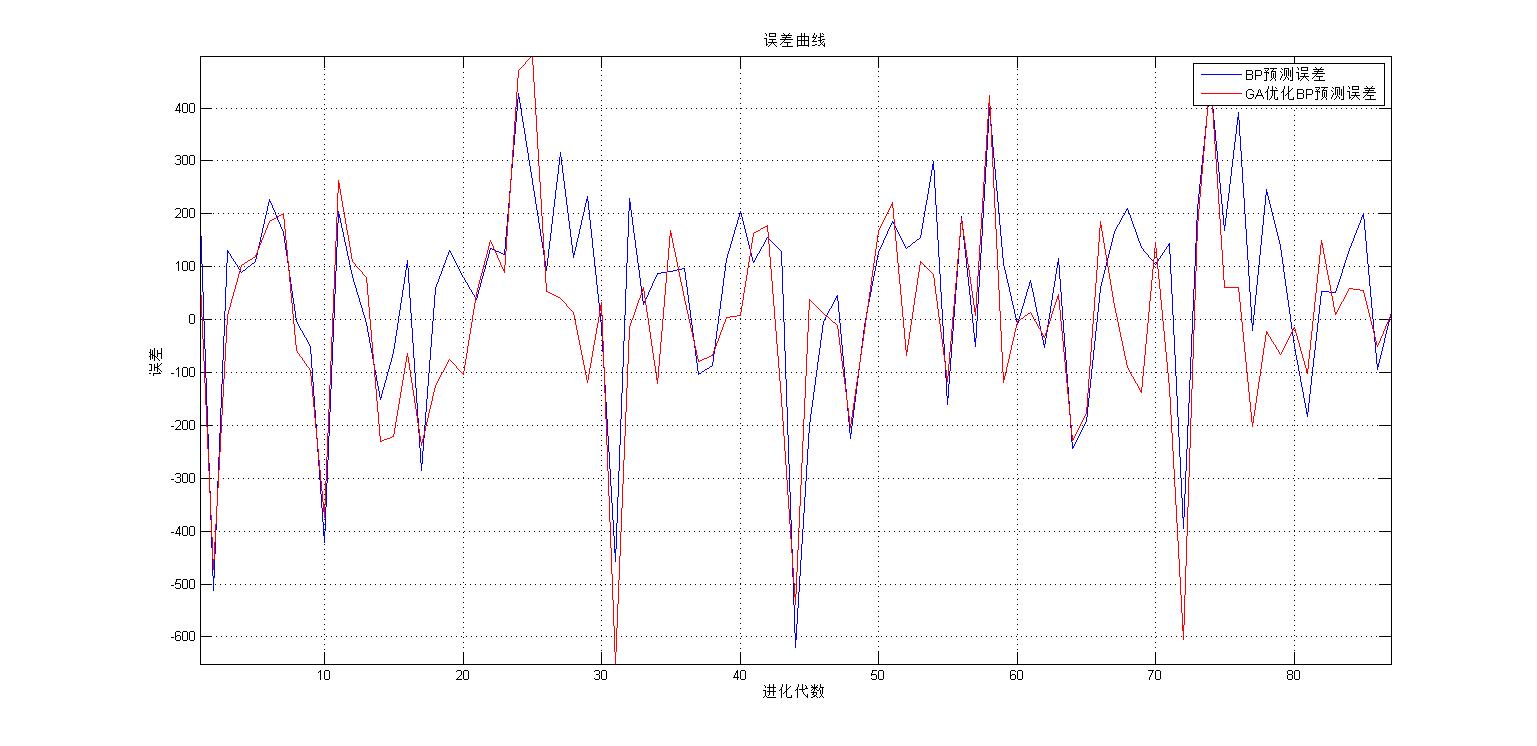
figure(8)
[r c]=size(BPerror);
plot([1:c],BPerror(1,:),'b-',[1:c],GBerror(1,:),'r-');
grid;
axis tight;
xlabel('进化代数');ylabel('误差');
legend('BP预测误差','GA优化BP预测误差');
title(['误差曲线']);

figure(9)
[r c]=size(BPerror);
plot( [1:c],BPmape(1,:),'b-',[1:c],GBmape(1,:),'r-');
grid;
axis tight;
xlabel('进化代数');ylabel('百分比误差');
legend('BP预测百分比误差','GA优化BP预测百分比误差');
title(['误差曲线']);


disp(['BP建模仿真时间为：' num2str(eBP) 's'] );
disp(['GA优化后BP再建模仿真时间为：' num2str(eGB) 's'] );
disp(['BP均方误差为：' num2str(BPmse)] );
disp(['GA优化BP均方误差为：' num2str(GBmse)] );
function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss                input  : 交叉概率
% lenchrom              input  : 染色体的长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% ret                   output : 交叉后的染色体
 for i=1:sizepop  %每一轮for循环中，可能会进行一次交叉操作，染色体是随机选择的，交叉位置也是随机选择的，%但该轮for循环中是否进行交叉操作则由交叉概率决定（continue控制）
     % 随机选择两个染色体进行交叉
     pick=rand(1,2);
     while prod(pick)==0
         pick=rand(1,2);
     end
     index=ceil(pick.*sizepop);
     % 交叉概率决定是否进行交叉
     pick=rand;
     while pick==0
         pick=rand;
     end
     if pick>pcross
         continue;
     end
     flag=0;
     while flag==0
         % 随机选择交叉位
         pick=rand;
         while pick==0
             pick=rand;
         end
         pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置，即选择第几个变量进行交叉，注意：两个染色体交叉的位置相同
         pick=rand; %交叉开始
         v1=chrom(index(1),pos);
         v2=chrom(index(2),pos);
         chrom(index(1),pos)=pick*v2+(1-pick)*v1;
         chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
         flag1=test(lenchrom,bound,chrom(index(1),:));  %检验染色体1的可行性
         flag2=test(lenchrom,bound,chrom(index(2),:));  %检验染色体2的可行性
         if   flag1*flag2==0
             flag=0;
         else flag=1;
         end    %如果两个染色体不是都可行，则重新交叉
     end
 end
ret=chrom;

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.