《Python数据科学手册》学习笔记及书评

Posted 2021-12-12 李英俊小朋友

《Python数据科学手册》学习笔记

文章目录

• 《Python数据科学手册》学习笔记
• • 写在前面
  • 1. 食谱数据库数据找不到的问题
  • 2.Seaborn马拉松可视化里时分秒转化为秒数的问题
  • 3. scikit-learn使用fetch_mldata无法下载MNIST数据集的问题
  • 4. GridSearchCV.grid_scores_和mean_validation_score报错
  • 5. Jupyter导出PDF从入门到绝望
  • 6. 机器学习部分笔记
  • • 6.1 判定系数
    • 6.2 朴素贝叶斯
    • 6.3 自举重采样方法
    • 6.4 白化
    • 6.5 机器学习章节总结
  • 7. 高斯过程学习笔记 / Gaussion Process

写在前面

• 封面

  

• 读后感

  • 只能说挺不错的，前面数据分析部分挺好，后面机器学习部分差点东西

1. 食谱数据库数据找不到的问题

• 问题：

  • 在P163页，3.11.3 案例：食谱数据库中，涉及到的食谱数据无法下载，在网上也找不到资源。是不是很揪心！！！是不是很绝望！！！
  • 我也是。。。然后我在网上搜了大概半个小时把，放弃了，然后慢慢看书上给的连接：食谱数据库
  • 我想，肯定有很多跟我看同一本书的歪果仁，在评论区吐槽没有数据。
  • 果然让我找到了解决办法。。。时隔多年，作者之一总算过来提供最新数据连接了。。。参考链接

• 结论：

  • 数据连接：https://s3.amazonaws.com/openrecipes/20170107-061401-recipeitems.json.gz

  • 下载方法：右键另存为就完事儿了。。。（链接都有了，再不会我就没辙了。。。）下完了然后右键解压缩。。。如图。。。

    

2.Seaborn马拉松可视化里时分秒转化为秒数的问题

• 抄作业

  在做Python Data Science Handbook的实例学习，4.16.3 案例：探索马拉松比赛成绩里，有提示将时分秒的时间化为秒的总数，以方便画图。书里给出的指令是：

  data[‘split_sec’]=data[‘split’].astype(int)/1E9

  data[‘final_sec’]=data[‘final’].astype(int)/1E9

  我用这种方式会出现以下错误：

  TypeError: cannot astype a timedelta from [timedelta64[ns]] to [int32]

• 结论

  • 描述的连接里面给出了一种解决办法，可是这种解决办法太复杂了，我想了一个更简单的

  • 先写一个将Timedelta格式的时间数据转化为总秒数的函数：

    data['split_sec'] = data['split'].apply(transfor_time)
    data['final_sec'] = data['final'].apply(transfor_time)
    

  • 然后对我们需要的列广播这个函数：

    data['split_sec'] = data['split'].apply(transfor_time)
    data['final_sec'] = data['final'].apply(transfor_time)
    

  • 查看结果：

    data.head()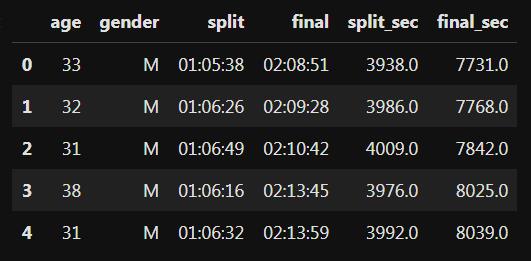
    

    

  • OK！完美解决。。。

3. scikit-learn使用fetch_mldata无法下载MNIST数据集的问题

• 问题：

  • 显示下载超时，链接不上，不能下载等

• 结论：

  • 直接下载MNIST数据集

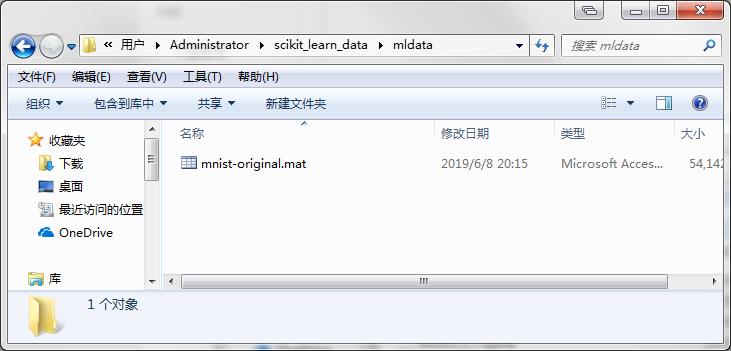
  • 把数据集保存到mldata文件夹中：

    

• 参考链接：Error Downloading MNIST #143

4. GridSearchCV.grid_scores_和mean_validation_score报错

• 问题：

  • 在P438页，5.13.4 示例：不是很朴素的贝叶斯中的2. 使用自定义评估器小节中有这样一行代码：scores = [val.mean_validation_score for val in grid.grid_scores_]

  • 运行之后报错：AttributeError: 'GridSearchCV' object has no attribute 'grid_scores_'

    

  • 经过百度了之后，可以知道grid_scores_在最新的sklearn中已经被弃用了，换成了cv_results_，参考链接

  • 那么，更改这个参数后，依然报错：AttributeError: 'str' object has no attribute 'mean_validation_score'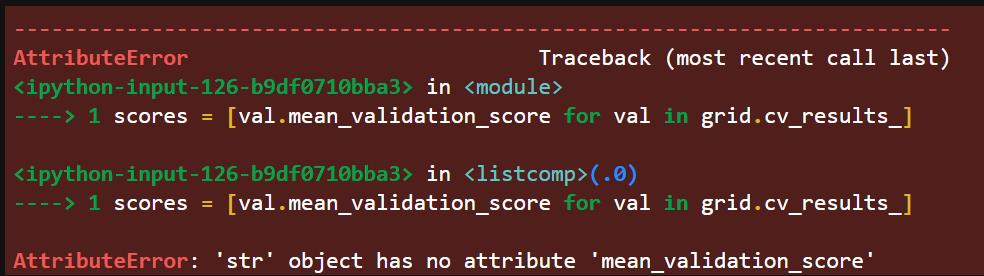

    

  • 这个问题就再也没有搜到好的解决方案了，所以我去查了GridSearchCV的文档

  • 然后发现，关于cv_results_的内容如下：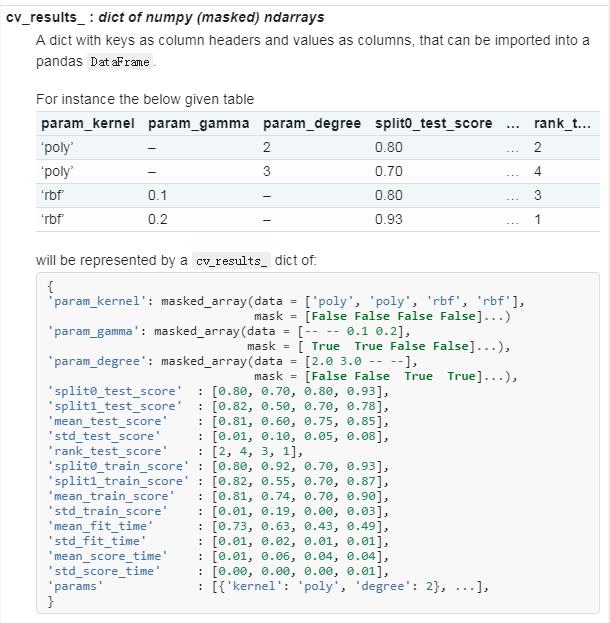

    

  • 这就很尴尬了，所以没有一个参数是包含validation关键字的，我的理解是，验证集和测试集在某种情况下可以认为是等价的。所以我猜测mean_validation_score对应的应该就是mean_test_score

  • 这样，原来的代码就改成了scores = grid.cv_results_['mean_test_score']

  • 为了证明我的猜想是正确的，所以，按照得到的scores结果，顺着其他的代码，知道最后绘图：

    

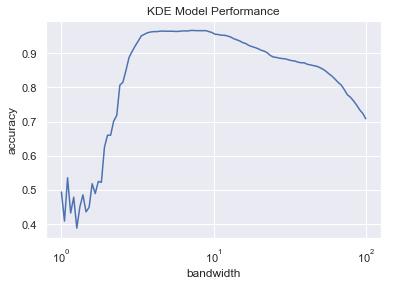
  • 事实证明，跟书上得到图一毛一样，所以证明我对源代码修改的猜想是正确的

  • 即证明了：

    • 旧版本代码：scores = [val.mean_validation_score for val in grid.grid_scores_]
    • 与新版本代码：scores = grid.cv_results_['mean_test_score']
    • 等价！

5. Jupyter导出PDF从入门到绝望

• 问题：

  • 我在使用jupyter lab的时候，想要把我的代码和结果导出成pdf格式的（由于里面有图片，所以不想导出成html）。然后报错：

    

  • 然后我用pip安装了pandoc，发现并没有什么luan用。并且好像跟报错所指的pandoc不一样。反正就是绝望就完事儿了

• 方案：

  1. 下载安装windows开发环境包的管理器，Chocolatey。参考官网了连接，用cmd粘代码就能装：官网

     @"%SystemRoot%\\System32\\WindowsPowerShell\\v1.0\\powershell.exe" -NoProfile -InputFormat None -ExecutionPolicy Bypass -Command "iex ((New-Object System.Net.WebClient).DownloadString('https://chocolatey.org/install.ps1'))" && SET "PATH=%PATH%;%ALLUSERSPROFILE%\\chocolatey\\bin"

  2. 然后呢，就可以用这个管理工具安装pandoc了，参考pandoc官网

     choco install pandoc

     

  3. 安装完事儿！

     

  4. 然后导出pdf的时候发现，竟然对pandoc的版本有要求，也是佛了，那就重新搞一下把。。。

     

     安装固定版本的pandoc，根据官网发布的版本list，我选择安装1.19版本的。choco install pandoc --version 1.19

     

     安装时安装完毕了，不知道为啥，一副好像报错了的样子，下的我赶紧去看一下到底是安装好了没。。。

     

     应该是完事儿了，然后试试导出pdf。

  5. pandoc好像是没有问题了，可是另一个包好像又除了问题：

     

     所以现在又要安装这个：

     choco install miktex

     

  6. 完。。。做完这一步，电脑自动重启了，然后jupyter lab打不开了，报错：

     ImportError: cannot import name 'constants' from 'zmq.backend.cython’

     然后没办法，用pip升级了一下pyzmq包，总算是能打开了。。。

     

     然后，告诉我，我下载的插件不能用了，要重新“build”，所以就重新安装了插件。。。（像显示目录啊之类的插件。。。）

     

     我真的很绝望。。。

     

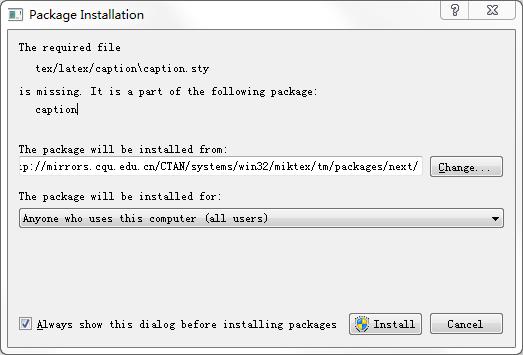
  7. 然后依然报同样的错误。。。于是我怀疑，是不是MikTex有错，于是在官网上下了一个exe安装的那种，一路确认下去。。。参考链接、下载链接

     果然，在点了导出pdf的时候，报错缺少的文件就弹出来安装程序了。。。

     

  8. 然后就成功保存pdf啦！

     

• 另辟蹊径

  说实话，这样导出来的pdf并不好看，还有一种方法，直接导出html，里面保留了插入的图片的那种，更能还原jupyter原来的排版。参考链接

6. 机器学习部分笔记

6.1 判定系数

1. 定义

   判定系数（coefficient of determination），也叫可决系数或决定系数，是指在线性回归中，回归平方和与总离差平方和之比值，其数值等于相关系数的平方。它是对估计的回归方程拟合优度的度量。（参考：百度百科）

   判定系数（记为R${}^2$）在统计学中用于度量因变量的变异中可由自变量解释部分所占的比例，以此来判断统计模型的解释力。对于简单线性回归而言，判定系数为样本相关系数的平方。

   假设一数据集包括$y_1,y_2,...,y_n$共n个观察值，相对应的模型预测值分别为$f_1,f_2,...,f_n$。定义残差$e_i=y_i-f_i$，

   平均观察值为：$\bar{y}=\frac{1}{n}\sum _{i=1}^n{y}_i$

   于是可以得到总平方和：$S{S}_{tot}=\sum _{i=1}(y_i-\bar{y}{)}^2$

   回归平方和：$S{S}_{reg}=\sum _{i=1}(f_i-\bar{y}{)}^2$

   残差平方和：$S{S}_{res}=\sum _{i=1}(y_i-f_i{)}^2=\sum _{i=1}{e}_i^2$

   由此，判定系数可定义为：$R^2=1-\frac{S{S}_{res}}{S{S}_{tot}}$

2. 总结

   R${}^2$ = 1：表示模型与数据完全吻合。

   R${}^2$ = 0：表示模型不比简单取均值好。

   R${}^2$ < 0：表示模型性能很差。

3. 系数标准

   判定系数只是说明列入模型的所有解释变量对因变量的联合的影响程度，不说明模型中单个解释变量的影响程度。
   判定系数达到多少为宜？没有一个统一的明确界限值；若建模的目的是预测因变量值，一般需考虑有较高的判定系数。若建模的目的是结构分析，就不能只追求高的判定系数，而是要得到总体回归系数的可信任的估计量。判定系数高并不一定说明每个回归系数都可信任。

6.2 朴素贝叶斯

1. 贝叶斯定理

   我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)求得P(B|A)的道路。

   $P(B|A)=\frac{P(A|B)P(B)}{P(A)}$

   推导：$P(A,B)=P(B|A)\ast P(A)=P(A|B)\ast P(B)$

   参考：机器学习之贝叶斯（贝叶斯定理、贝叶斯网络、朴素贝叶斯）

   朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素。

   朴素贝叶斯的思想基础是这样的：**对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。**通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人&#x

   以上是关于《Python数据科学手册》学习笔记及书评的主要内容，如果未能解决你的问题，请参考以下文章

   《流畅的python》学习笔记及书评

   《流畅的python》学习笔记及书评

   《TensorFlow实战Google深度学习框架（第二版）》学习笔记及书评

   《TensorFlow实战Google深度学习框架（第二版）》学习笔记及书评

   《TensorFlow实战Google深度学习框架（第二版）》学习笔记及书评

   《Python数据科学手册》异常校正