nil Foundation的基于Solana light client实现的zk-bridge方案

Posted 2021-12-12 mutourend

1. 引言

前序博客有：

• Solana light client

nil Foundation认为，Solana 9月的爆发源于 Ethereum-Solana bridge——Wormhole，但是该bridge需依赖bridge内节点间的PoA共识 并 需要在pool合约中存入足够的资金，详细可参看博客：

• Wormhole资产跨链项目代码解析

针对由Solana->Ethereum的情况，为了实现trustless，可为：

• Solana端生成的数据可在Ethereum的EVM直接验证，即Solana端生成的数据可证明其确实已锁定了某资产，而Ethereum端EVM验证通过后即可mint相应的资产。

nil Foundation认为是其首次提出了：tokenless zero-knowledge proof system-based in-EVM Solana “light client” state verification.

2. 现有zk-bridge

当前的zk-bridge 方案都需要token，用于保证：

• 1）由某个可信任的人正确生成a data-source cluster state proof
• 2）将该proof “Often enough” 提交到receipt cluster中。

“Often enough” 增加了proof generation 的复杂性——意味着生成proof的relay cluster members的硬件要满足一定的性能（通常为高级的GPU甚至FPGA）才能生成state proofs。这种硬件投入需要token来激励relay cluster members。

同时还有in-EVM state proof verification costs，传统方法是也有这些受激励的成员来支付。

3. nil Foundation的zk-bridge方案

由Solana端来生成state proof，就不再需要由一组PoA节点来生成VAA，从而无需对PoA节点进行激励，也就不需要token。

in-EVM-verifiable的Solana state proof中的state为“light client” state，比Solana validator节点中的state更小，包含有：

• validator votes
• validator stakes
• transaction inclusion proof等。

这就意味着无需验证整个Solana database，仅需验证其关键的一部分，从而可大幅减小circuit size，最终缩短生成proof和验证proof的时间。

为了减少生成和验证proof的计算量，需要减少proof system中的constraints/gates数量。基于此，生产light client state proof的proof system通常是基于PLONK而不是R1CS，因为 基于PLONK的proof system 比 基于R1CS的proof system 节约5倍的coonstraints/gates。

尽管，constraints的数量并不是影响proof size的唯一因素。所选择的commitment scheme可决定proof size，也可决定proof生成和验证的计算复杂度。这就意味着需在 proof生成时间 与 proof验证时间 之间进行平衡取舍。

基于PLONK的proof system，若采用Kate commitment scheme，其具有最优的constant-time verification complexity。但是存在的问题是需要trusted setup。

更优的方案是，采用 RedShift构建FRI commitment（如STARKs所用） + PLONK-based proof system。RedShift介绍了LPC commitment scheme，其verify proof time少于$21\times log2(n)$，生成proof time少于$54(n+a)log2(n+a)$，具体取决于PLONK rows的数量。

这种proof生成/验证机制，任何人都可自己生成并提交bridge所需的Solana state proof。

3.1 安全措施

为了保证实际操作的安全性，需要为in-EVM proof submission和verification 过程引入一些安全措施。

in-EVM verificator应可check：

• if the state proof is derived from the previous one, which is derived from a previous one, which is derived from a previous one and so on.

state proof sequence的维护机制为：
令$B_{n_1}$为the last state confirmed on Ethereum，Prover想confirm a new $B_{n_2}$ state。令$H_B$为state $B$的bank hash。proving statement中包含但不限于以下要点：

• 1）Show that the validator set is correct。
• 2）Show that the $B_{n_1}$ corresponds to the last confirmed state on Ethereum。
• 3）对于$i\in [n_1+1,n_2+31]$，需Show that $B_i$ contains $H_{B_{i-1}}$ as a hash of the previous state。
• 4）对于$i=n_2$，需Show that there are enough valid signatures from the current validator set for $B_i$。
• 5）Build a Merkle Tree $T_{n_1,n_2}$ from $H_{B_{n_1}},\cdots ,H_{B_{n_2}}$。

$T_{n_1,n_2}$ 可提供a successful transaction from $B_{n_1},\cdots ,B_{n_2}$ to the Ethereum-based proof verificator。

如何证明步骤1）中的validator set是正确的呢？当前Solana并未实现 Solana已接收提案——Simple Payment and State Verification。

当前的最优方案为：
The best way to prove that the validator set from some Solana epoch is derived and consistent with the previous one is “anchor” transactions. It is the transaction that checks the validator’s account state. The prover needs to send such transactions periodically at the end of epochs. It allows decreasing the number of blocks between the last known account state and the new epoch.

但Solana当前并未实现anchor类型的交易。若 Solana已接收提案——Simple Payment and State Verification 已实现，整个证明validator set correct的过程就会简单很多。

4. zk-bridge中单笔交易的开销

Solana中的Validator votes采用的是Ed25519签名，Ed25519验签过程中需要1个fixed base scalar multiplication和2个variable base scalar multiplication。此外，每个Ed25519签名中还有SHA2-512计算。

根据 https://zcash.github.io/orchard/design/circuit/gadgets/ecc.html 可知：

• 1）Fixed base scalar multiplication 需要$f=255/6$ gates。
• 2）Variable base scalar multiplication 需要$v=255/2$ gates。

SHA2-512使用PLONK计算需要约2万个gates。

验签过程中会生成 $n_{rows-1}=N_{sig}\cdot (f+2\cdot v+H)$ rows。其中$H$为SHA256 hash函数所用的行数，$N_{sig}$为签名数量。

Solana中需要进行Hash Chain证明和Merkle TreeZHENGM，为此，需要额外增加$n_{rows-2}=2\cdot (n_2-n_1)\cdot H_{sha256}+\log (n_2-n_1)\cdot H_{sha256}$ 行。此处，为简化计算，为$T_{n_1,n_2}$选用的为SHA256 hash函数，也可以改为Poseidon hash函数。

总的计算量为：

• 1）验证Merkle tree proof的cost为${\log }^{2}n+2\cdot \log 2n$
• 2）low-degree testing $(\log n)$。其中$n$为committed polynomial’s degree （$n=rows\cdot (wires+1)$）。

简化来说，主要的cost来源于low degree test，因为其包含了2个有限域内的倒数运算，约需要30000 gas，Keccak256需要30 gas。
特别地：

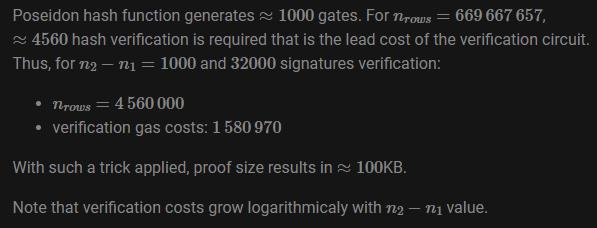
按上述方式，EVM中进行state proof verification 所需gas约为2014200。

为此，可通过减少proof size 和verification costs来降低gas费，可能的方法之一是add one more proof layer。
RedShift proof 可通过另一个RedShift instance 来verify。相当于“proof of correct proof of knowledge”。

参考资料

[1] Solana已接收提案——Simple Payment and State Verification
[2] 用于Solana-Ethereum的zk-bridge方案——=nil; Foundation’s In-EVM Solana Light-Client State Verification