数据结构 ---[实现堆(heap)(包含方法图解过程) 优先队列(Priority Queue)]

Posted 2021-12-12 小智RE0

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构 ---[实现堆(heap)(包含方法图解过程) 优先队列(Priority Queue)]相关的知识，希望对你有一定的参考价值。

文章目录

1.堆 ,满二叉树,完全二叉树(概论)

之前已经学过队列的知识;知道队列是先进先出(FIFO)结构的;那么优先队列即就是和优先级有关的队列;优先级高的元素首先会出队;

在学习优先队列之前,先学习堆的知识;因为可以用堆作为优先队列的底层数据结构;

这个优先级问题的话,不是绝对固定的,可以指定一个规则;规定怎么样优先级高,怎么样优先级低

由于堆是一棵完全二叉树;
那么,首先要学会满二叉树和完全二叉树的知识;

满二叉树

除了叶子节点之外,其余的节点都具有左子树和右子树;
叶子节点都位于最后一层;
每层节点的个数为 2^(层数-1) ;这个层数是由1开始的;
满二叉树树的叶子节点总数为 2 ^ (高度 -1) ;树的高度(即总层数)
满二叉树的非叶子节点总数为[ 2 ^ (高度 -1 )] -1 ;
满二叉树的节点总数为[ 2 ^(高度)] -1

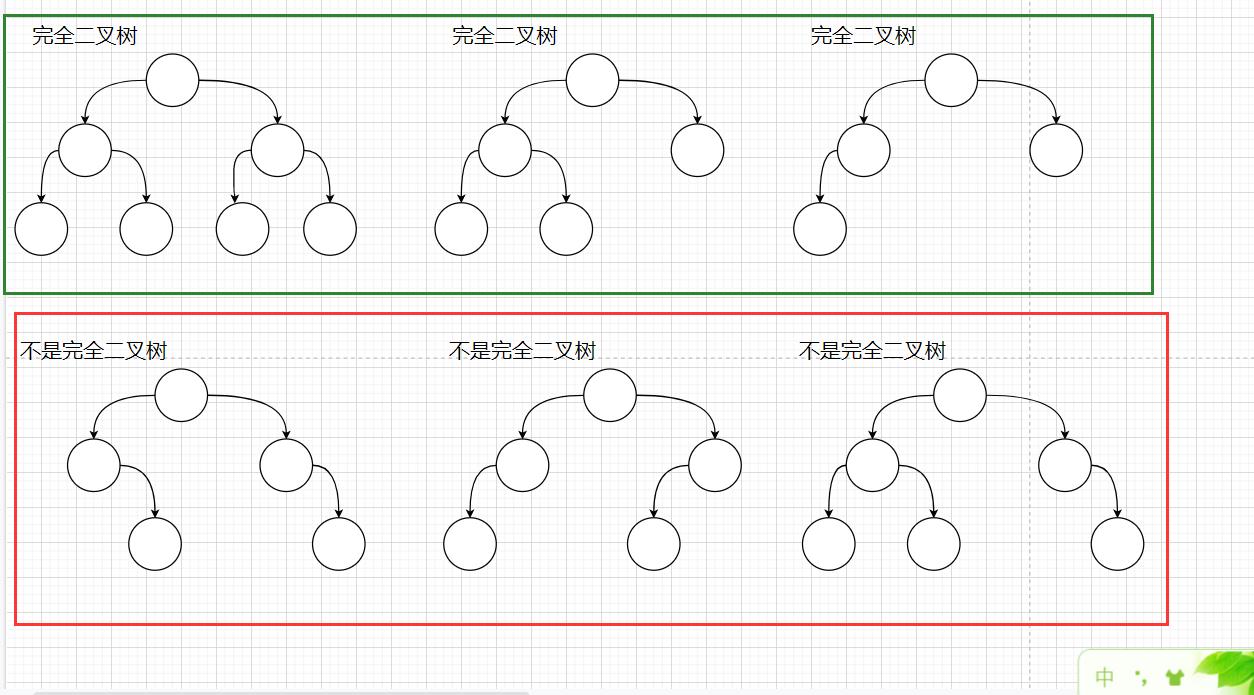
完全二叉树

按照树的结构;从左到右依次排列;
叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。
需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树

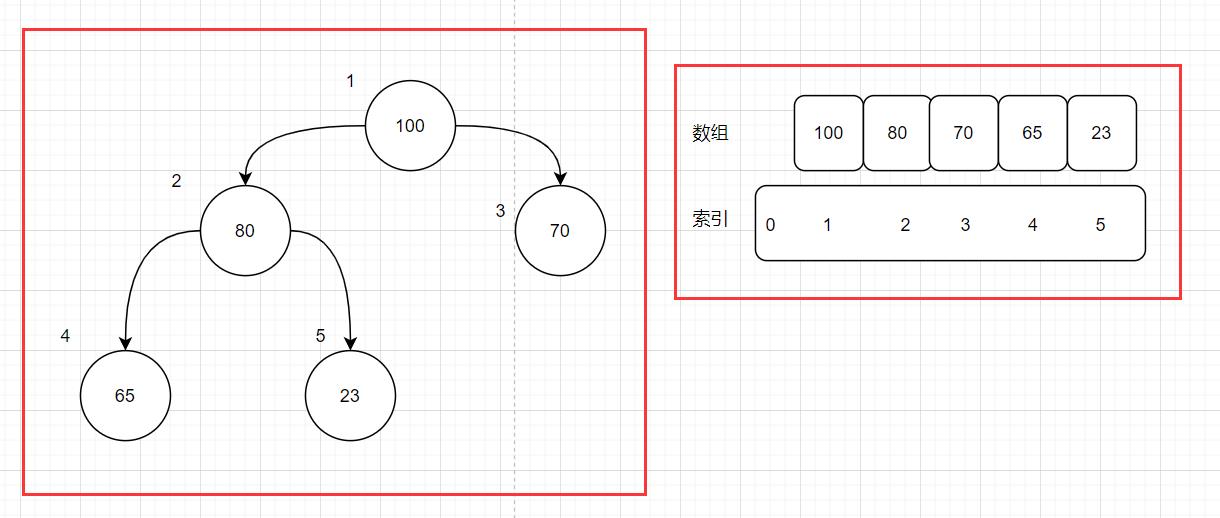
那么堆是什么呢

堆

是一棵完全二叉树;
堆中的父节点大于等于子节点的优先级[最大堆] ;或者堆中的父节点小于等于子节点的优先级[最小堆];
堆可以看做一棵树的数组对象 ;

本次主要学的是最大堆;提前规定一下,数值大的优先级最高

比如,这样的就可看做是个最大堆

那么这时就可以来推导一下了;
若是从索引由1开始;

根结点没有父节点;
那么除过根节点之外的节点 ; 这个节点的父节点索引就是 ParentIndex = (当前结点索引/2);
只要是有左右结点的节点 ; 这个结点的左结点索引就是 leftIndex = (2 * 当前结点索引);这个结点的右结点索引就是rightIndex = ( 2 * 当前结点索引) + 1 = leftIndex +1;

若是索引由0开始

根结点没有父节点;
那么除过根节点之外的节点 ;
- 这个节点的父节点索引就是ParentIndex = [(当前结点索引-1) / 2];
只要是有左右结点的节点 ;
- 这个结点的左结点索引就是 leftIndex = ( 2 * 当前结点索引) +1;
- 这个结点的右结点索引就是rightIndex = ( 2 * 当前结点索引) + 2 = leftIndex +1;

2. 具体实现最大堆

2.1初始化的几个方法;判断空堆;查询父节点索引,查询左/右结点索引的方法

首先是基础的几个方法

import java.util.Arrays;
/**
 * @author by CSDN@小智RE0
 * 自定义最大堆 ;优先级高的(数值大的)在上面
 */
 //由于要对元素的数值进行比较,那么这里就得继承这个类,保持可比性
public class MaxHeap  <T extends Comparable<T> > {
    //使用数组作为底层数据机构;
    private  T[] data;
    //元素的实际个数;
    private  int size;
    //构造方法初始化;
    public MaxHeap() {
        this.size = 0;
        this.data = (T[]) new Comparable[100];
    }

    public MaxHeap(T[] array) {
        if(array == null || array.length==0) return;
        //复制一份数组;
        this.data = Arrays.copyOf(array,array.length);
        this.size = array.length;
    }

    //判空;
    public boolean isEmpty(){
        return this.size == 0;
    }

    //查询元素实际个数;
    public int getSize(){
        return this.size;
    }

    //查询父节点的索引;
    public int getParentIndex(int index){
        //需要排除根结点的索引;
        if(index == 0) return -1;
        //索引异常;
        if(index < 0) throw new RuntimeException("Index out of bounds");

        return (index - 1)/2;
    }

    //查询指定结点的左结点索引;
    public int getLeftIndex(int index){
        if(index < 0) throw new RuntimeException("Index out of bounds");
        return (2*index)+1;
    }

    //查询指定结点的右结点索引;
    public int getRightIndex(int index){
        if(index < 0) throw new RuntimeException("Index out of bounds");
        return (2*index)+2;
    }
   
    // 获取优先级最高的节点;
    public T getFrontNode() {
        return isEmpty() ? null : this.data[0];
    }
}

2.2 最大堆的添加节点方法

方式1:添加时进行交换

📢图解

比如说,需要添加元素 300;先把这个元素存进去;
通过初次观察,这个300的值已经大于它的父节点66;大于66的父节点80;甚至大于根结点121;
即这个300优先级过高,这个300就得向上浮动

(1)首先,向上浮动;300和66交换位置

(2)然后再向上浮动;300再和80交换位置

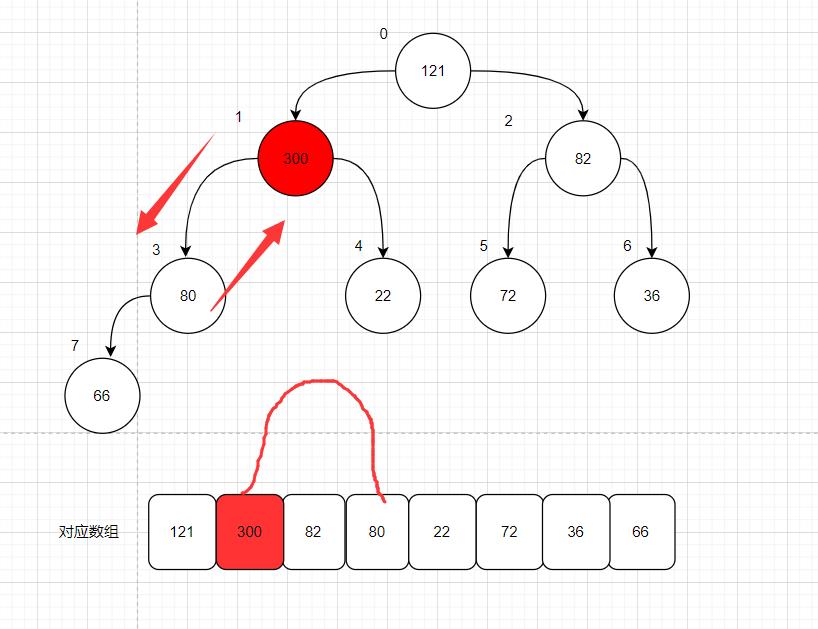
(3)再向上浮动; 300 和121 交换;整个添加元素完成

这个向上浮动的话,不能一直浮动;肯定有终结点;那么可分为两种情况啊;
(1):浮动到达根结点了;即数组的索引都到0了;
(2):向上浮动时;父节点优先级已经大于这个结点的优先级了,那就停止浮动;

原理大概就是这样,试试看

用代码实现堆中元素添加(方式1—交换式);以及输出堆的方法

在刚才自定义的堆MaxHeap中编写

/**
 * 添加节点的方法; 注意添加进去后,要按照最大堆的规定,优先级高的在上面;
 * 下面先采用方式1(交换式); 其中会搭配 元素上浮方法1; 以及交换元素的方法;
 * @param ele 添加的元素
 */
public void addEleMethod1(T ele){
    //先把元素挂接到树上;
    data[size] = ele;
    size+=1;
    //调用 元素上浮方法1;
    floatUp1();
}


/**
 * 元素上浮方法1;
 */
private void floatUp1(){
    //这个刚刚添加的元素索引;
    int currentIndex = size-1;
    //先获取这个刚添加的元素的 父节点索引;
    int parentIndex = getParentIndex(currentIndex);
    //若当前节点的值比父节点还大,就一直交换;
    while (currentIndex >0 && data[currentIndex].compareTo(data[parentIndex])>0){
        //交换节点和它的父节点;
        swapEle(data,currentIndex,parentIndex);

        //更新当前结点与父节点;
        currentIndex = parentIndex;

        parentIndex = getParentIndex(currentIndex);
    }
}

/**
 * 数组内交换元素的方法;
 * @param array 数组
 * @param pre   要交换的节点索引;
 * @param res   被交换的节点索引
 */
private void swapEle(T[] array,int pre,int res){
    //用一个临时变量作为中介;
    T temp =array[res];
    array[res] = array[pre];
    array[pre] = temp;
}


/**
 * 输出堆元素的方法;
 * @return
 */
@Override
public String toString() {
    StringBuilder stringBuilder = new StringBuilder();
    stringBuilder.append("[");
    for (int i = 0; i < size; i++) {
        stringBuilder.append(data[i]);
        if(i!=size-1){
            stringBuilder.append("->");
        }
    }
    stringBuilder.append("]");
    return stringBuilder.toString();
}

进行测试

//测试;
public static void main(String[] args) {

    //加入堆结构;
    MaxHeap<Integer> maxHeap = new MaxHeap<>();
    //测试添加方法1;  交换式
    maxHeap.addEleMethod1(121);
    maxHeap.addEleMethod1(80);
    maxHeap.addEleMethod1(82);
    maxHeap.addEleMethod1(66);
    maxHeap.addEleMethod1(22);
    maxHeap.addEleMethod1(72);
    maxHeap.addEleMethod1(36);
    System.out.println("原先的队列-->");
    System.out.println(maxHeap);

    maxHeap.addEleMethod1(300);
    System.out.println("添加元素 300 后的队列-->");
    System.out.println(maxHeap);
}

测试结果;和分析的结果是一样的

原先的队列-->
[121->80->82->66->22->72->36]
添加元素 300 后的队列-->
[300->121->82->80->22->72->36->66]

方式2:添加时进行覆盖

📢图解

原理差不多,在添加元素之后,不再是让元素进行交换;而是比较优先级之后,
若这个要添加的元素的优先级比它放入的索引位置的父节点优先级高,那就让父节点的值覆盖这个添加节点的位置,(注意,这里不要担心,因为要添加的节点值是已知的)依次类推,直到找到合适位置,再把这个添加的节点放到合适的位置;
还是用刚才添加元素300 的案例来看

(1) 首先,向上浮动,比较的是300 和 66 ;由于300大于66,那就让66的值覆盖当前操作节点300的位置;
这时记得要更改300的索引为3;
或者理解方便一点;即更新要操作的节点位置索引由7 -----> 3 ;相对应的,下次操作节点的父节点索引也就是1的位置

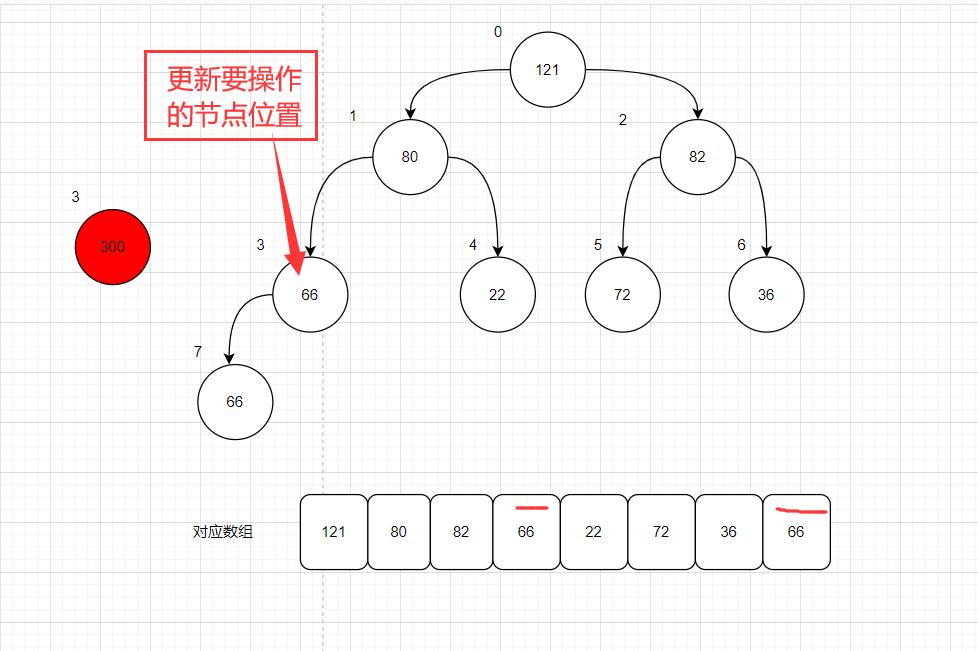
(2)首先,注意上面说了,这次操作的节点已经更新到索引位置为3了
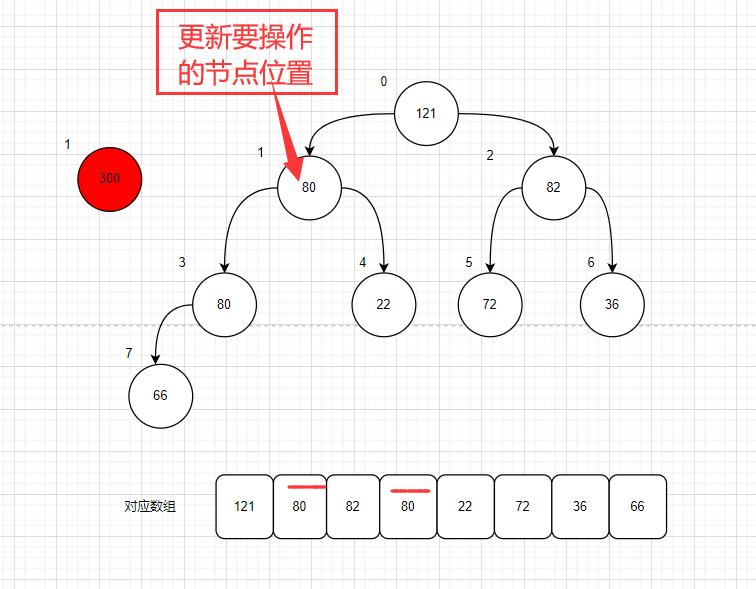
这时,再次向上浮动,会比较 300 和 80 ;由于 300 大于 80 ,那就让80 的值覆盖当前操作节点30;
然后注意,此时要操作的节点位置更新 3-----> 1;操作位置的父节点也更新到索引0的位置

(3) OK,继续向上浮动;比较300 和121 ;由于 300 大于 121,那么就让121的值覆盖操作节点索引1的位置;注意这里还更新了要操作的节点位置1----->0

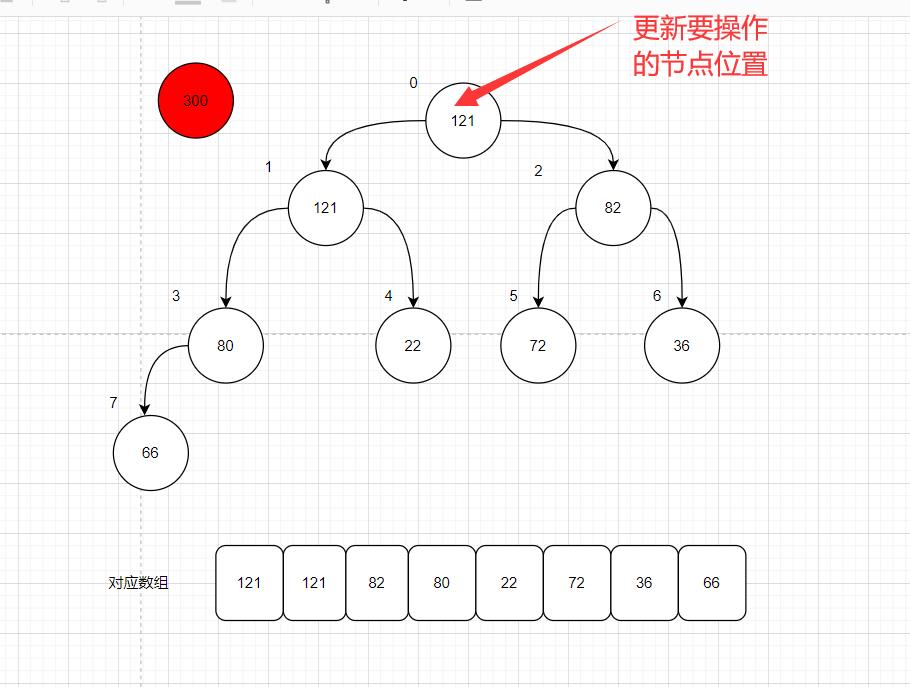
OK,这时注意到,操作节点索引为0;已经到根结点了,该收手了!
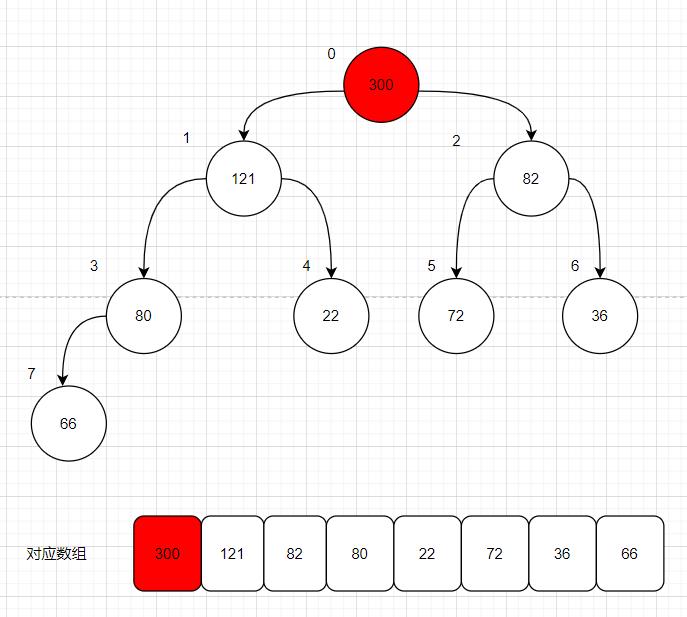
那么,300也就勉为其难地住进了这个堆;
把300放到操作节点索引为0的位置;

用代码实现堆中元素添加(方式2 —覆盖式);

这次输出方法就不在这放了;上面写过了
在刚才自定义的堆MaxHeap中编写

/**
 * 添加节点的方法2;
 * @param ele 添加的元素
 */
public void addEleMethod2(T ele){
    //先把元素挂接到树上;
    data[size] = ele;
    size++;
    //调用 元素上浮方法2; 这里需要传递要添加的元素;
    floatUp2(ele);
}
/**
 * 元素上浮方法2;
 * 在这个方法内,不是进行元素交换,而是要进行覆盖,只要这个要添加的元素比上面的大,
 * @param ele 指定要添加的元素;
 */
private void floatUp2(T ele){
    //刚添加的元素位置 ; 或者可以说这个currentIndex 表示要操作的节点索引;
    int currentIndex = size -1;
    int parentIndex = getParentIndex(currentIndex);
    //注意这里比较时,一直用的是添加的节点 和 父节点进行比较;
    while (currentIndex > 0 && ele.compareTo(data[parentIndex])>0){
        //让父节点的值覆盖操作的节点;
        data[currentIndex] = data[parentIndex];
        //更新操作的节点;
        currentIndex = parentIndex;
        //父节点的索引更新;
        parentIndex = getParentIndex(currentIndex);
    }
    //切记,这里需要把添加的索引放到最后一次更新的操作节点索引位置;
    data[currentIndex] = ele;
}

也来测试一下,注意用添加方法2

//测试;
public static void main(String[] args) {
    //加入堆结构;
    MaxHeap<Integer> maxHeap = new MaxHeap<>();
    //测试添加方法2; 覆盖式
    maxHeap.addEleMethod2(121);
    maxHeap.addEleMethod2(80);
    maxHeap.addEleMethod2(82);
    maxHeap.addEleMethod2(66);
    maxHeap.addEleMethod2(22);
    maxHeap.addEleMethod2(72);
    maxHeap.addEleMethod2(36);
    System.out.println("原先的队列-->");
    System.out.println(maxHeap);
    maxHeap.addEleMethod2(300);
    System.out.println("添加元素 300 后的队列-->");
    System.out.println(maxHeap);
}

测试结果;OK

原先的队列-->
[121->80->82->66->22->72->36]
添加元素 300 后的队列-->
[300->121->82->80->22->72->36->66]

2.3 在最大堆取出优先级最高的节点方法

定义这个最大堆的时候就已经提前规定了啊;这个值越大的优先级高,那么根结点的优先级是最高的;

这个根结点取出之后;由于这是个堆,那么它还要保持原来的结构,即上面的优先级高;
即删除了根结点后,还要让其他的结点按照优先级进行修改;

这边也是两种方式;交换式和覆盖式;

方式1:交换式

在取出优先级最高的根结点后;先把最后一个结点的值移动到根结点的位置;然后再向下进行比较;优先级比它大的,就和它进行交换,…
这个停止的条件就是:
(1)到达叶子节点(没有左右结点,注意的是完全二叉树是由左至右的,所以首先判断是否有左节点即可,不满足就停止了);
(2)或者遇到优先级比它还小的节点;

📢图解

比如说,我这里有个最大堆;我需要把优先级最高的节点 800取出;那么就得准备把最后一个节点200放到根结点的位置

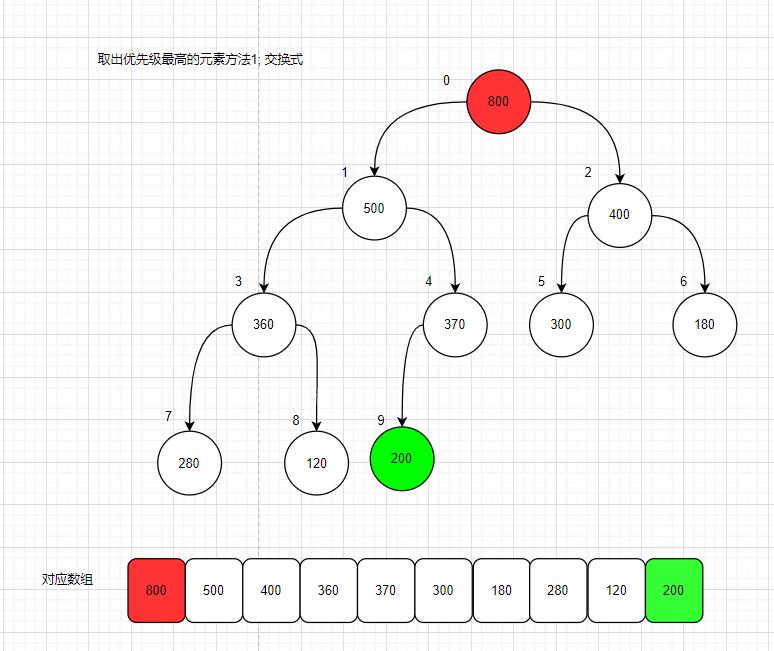
(1)当然,先把根结点800取出;最后一个节点200放到根结点的位置;
看看200这位置明显不合适

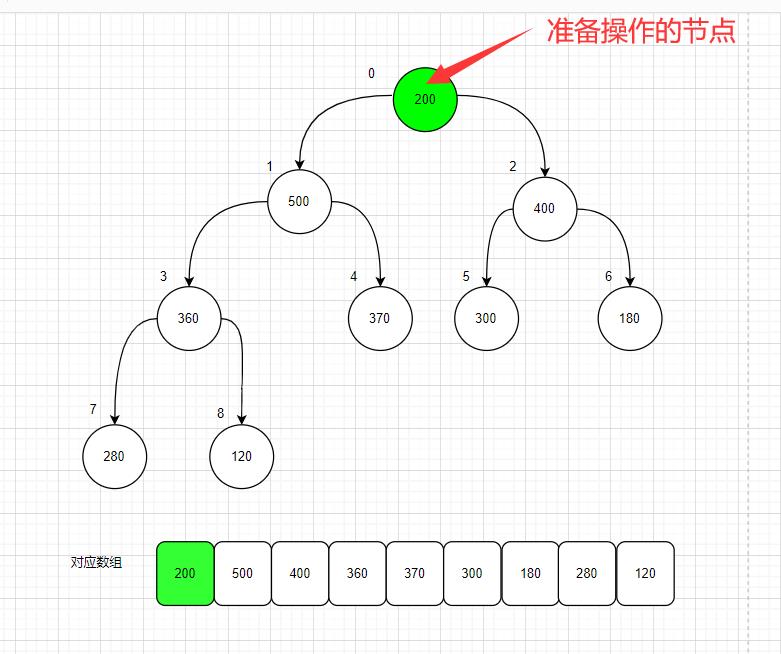
(2)通过比较索引为0的的节点200;左结点优先级和右结点优先级比较后;发现左节点500的优先级最高;
好,就把200 和500交换了;
更新下次要操作的节点位置;

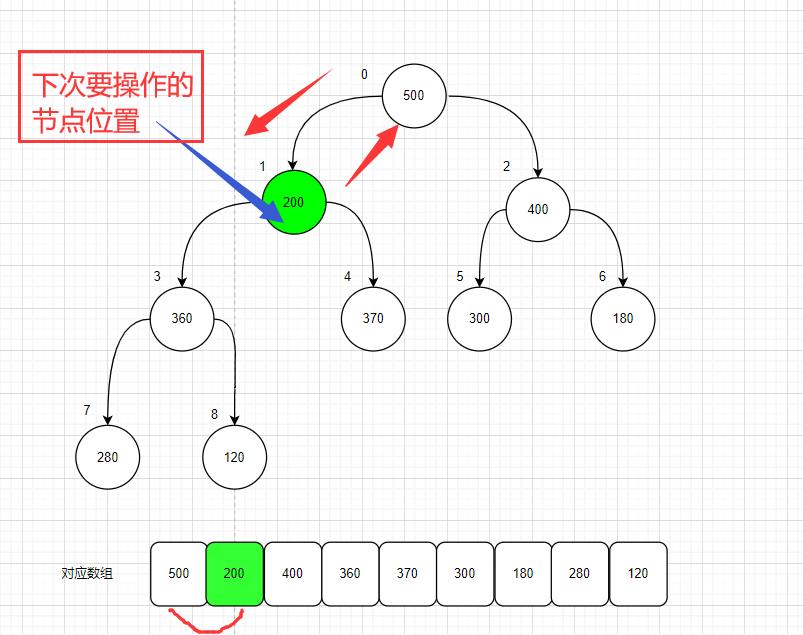
(3)比较索引为1的节点 200 ;比较它的左节点优先级和右结点优先级,发现右结点370优先级较高,
号,那就让200和370进行交换;
这时,还会更新下次要操作的节点位置为4

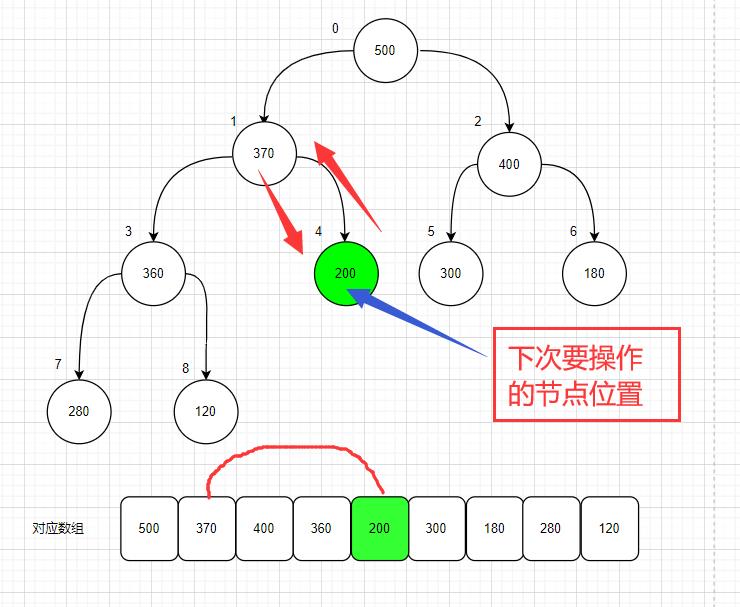
(4) 到这里,判断的时候,诶;发现他没有子节点了;那么好了,完成

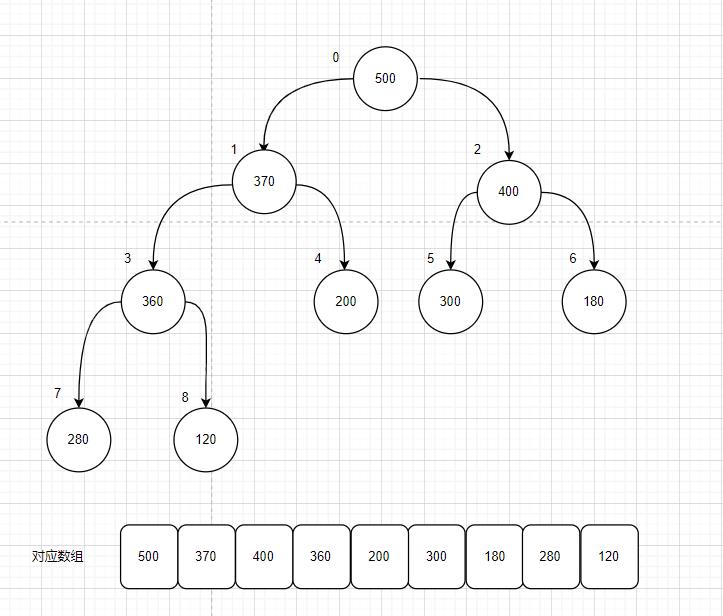
用代码实现在最大堆中取出最高优先级的节点 (方式1–交换式)

注意,这其中进行交换的时候,用的交换方法还是前面那个数组内的元素交换方法;

在刚才自定义的堆MaxHeap中编写;
这里调用的swapEle()交换数组内元素方法是之前写的;

/**
     * 取出优先级最高的节点 方法1;
     * 下面会调用元素下移方法 1;
     */
    public T pollMaxPriorityMethod1() {
        //先判空;
        if (isEmpty()) throw new RuntimeException("This heap is empty");
        //取出的是最高优先级节点--根结点;先存入临时变量;
        T temp = this.data[0];
        //将最后一个元素放到根结点的位置;
        this.data[0] = data[size - 1];
        //然后再减少实际元素的个数;
        size -= 1;

        //调用元素下移 方法 1 ;
        moveDown1();
        //最终返回这个最高优先级的
        return temp;
    }

    /**
     * 元素向下移动 方法 1;
     */
    private void moveDown1() {
        //万一刚删除后,这个堆就为空了;就不必操作了;
        if (isEmpty()) {
            return;
        }
        //需要操作的节点位置;
        int currentIndex = 0;
        //左子节点;
        int leftIndex = getLeftIndex(currentIndex);
        //右子节点;
        int rightIndex = getRightIndex(currentIndex);

        //左右子节点比较优先级后的高优先级节点索引; 首先默认为左节点;
        int maxPriorityLeftRight = leftIndex;

        //找合适位置,直到遇到优先级比它小的;或者到达叶子节点;
        //有左节点的话就进行操作;
        while (leftIndex < size) {
            //当右结点的优先级高于左节点时,更新这个最高优先级节点的索引;
            if (rightIndex < size && data[leftIndex].compareTo(data[rightIndex]) < 0) {
                maxPriorityLeftRight = rightIndex;
            }

            //这里加上结束的判断;遇到优先级比它小的;直接结束;
            if (data[currentIndex].compareTo(data[maxPriorityLeftRight]) > 0) {
                return;
            }

            //进行交换; 注意交换的是这个当前操作节点和左右结点中优先级较高的节点;
            swapEle(data, currentIndex, maxPriorityLeftRight);

            //更新要操作的节点;
            currentIndex = maxPriorityLeftRight;
            //更新左节点,右结点;以及最高优先级节点的索引;
            leftIndex = getLeftIndex(currentIndex);
            rightIndex = getRightIndex(currentIndex);
            maxPriorityLeftRight = leftIndex;
        }
    }

测试使用

//测试;
public static void main(String[] args) {

    //加入堆结构;
    MaxHeap<Integer> maxHeap = new MaxHeap<>();
    //测试添加方法2;
    maxHeap.addEleMethod2(800);
    maxHeap.addEleMethod2(500);
    maxHeap.addEleMethod2(400);
    maxHeap.addEleMethod2(360);
    maxHeap.addEleMethod2(370);
    maxHeap.addEleMethod2(300);
    maxHeap.addEleMethod2(180);
    maxHeap.addEleMethod2(280);
    maxHeap.addEleMethod2(120);
    maxHeap.addEleMethod2(200);
    SystemJVM内存—堆（heap）栈（stack）方法区（method）  (转)
 堆（heap）栈（stack）方法区（method）
 heap 堆
 Jvm（14.2），运行时数据---堆,栈,方法区
 堆(heap)栈(stack)和方法区(method)
 数据结构：堆（Heap）

数据结构 ---[实现 堆(heap)(包含方法图解过程) 优先队列(Priority Queue)]