（递归记忆化）最好与最坏的选择——375. 猜数字大小 II

Posted 2021-12-12 C_YCBX Py_YYDS

文章目录

• • 题目
  • 题目解析
  • 解题代码

题目

OJ平台

题目解析

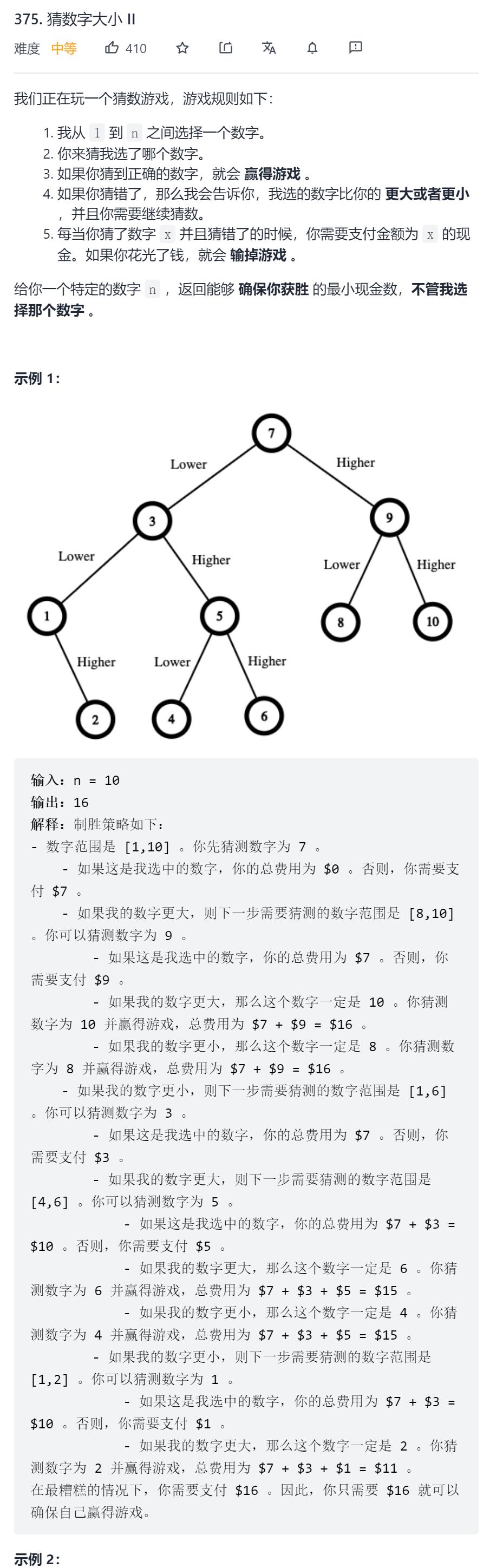
• 刚开始看到这个给出的示例图，我还以为就是二分的分治。。。

后面看了题解，发现是一个 爆搜+记忆化 的过程，关于如何去爆搜呢？

确保获胜的最小现金数？确保获胜代表这个选择次数不能够是最优，因为如果这样的话，那完全就可以选择一次就猜中，就这就不算是确保获胜了。我们需要模拟一个过程，这个过程就是你每次的猜测，只要有可能出错，则让他出错（然后就交现金了），直到出现必然获胜的时候，则得出所耗费的现金情况。也就是确保获胜导致的最终结果就是必定获胜的情况下（往左选择或者往右选择的情况下），在左边或者右边选择下（每次的左右选择都是最优）花费较高的选项则为确保获胜最小现金数。

对应到代码上来就是：每一次的选择都要是最优（树的根定位最优），而整个选择次数和花费需要是最坏（树的左右子树取结果大的那个）。

很明显这样爆搜肯定会直接超时，毕竟按这样算的话应该有 $O(n\ast 2^n)$ 的复杂度！

而由于每个树都是根据一个范围来取的，只要范围一确定算出来的结果肯定是相同的，所以直接可以记忆化！

解题代码

//记忆化过程思路：每一层递归代表一个子树，而我们最优的根还不清楚，每个根状态需要取最小值，而对于左右子树的状态我们则需要取最大值。
// 这题又谷歌扔鸡蛋那题的味道了
int N;
inline int max(int a,int b){
    return a>b?a:b;
}
int dfs(int dp[][N+2],int l, int r){
    if(l>=r)
        return 0;
    if(dp[l][r])
        return dp[l][r];
    int res = INT_MAX;
    for(int i=l;i<=r;i++){//枚举根节点可能的最优情况，而左右子树取大的那一个情况。
        int cost = i+max(dfs(dp,i+1,r),dfs(dp,l,i-1));
        
        res = fmin(cost,res);
    }
    return dp[l][r] = res;
}
int getMoneyAmount(int n){
    N = n;
    int dp[n+2][n+2];
    memset(dp,0,sizeof(dp));
    return dfs(dp,1,n);
}