Weiler-Atherton算法计算机图形学多边形裁剪算法

Posted 2021-12-12 kaka0010

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Weiler-Atherton算法计算机图形学多边形裁剪算法相关的知识，希望对你有一定的参考价值。

什么是多边形裁剪

通常来说就是利用多边形来裁剪多边形的一种方法，一般情况下是利用矩形来裁剪凹凸多边形

凸多边形
凹多边形

上面红色划线部分就是裁剪出的部分

前置知识

OPENGL基础语法
基本上就是一些画线和画多边形的操作，难度较低
求两直线交点
较为基础的数学知识
求一个点是否落在多边形内/外
计算几何知识
Weiler-Atherton多边形裁剪算法

这里着重介绍Weiler-Atherton算法，其余不懂的可以先学会再看。

算法步骤

首先绘制两个相交的多边形
对于多边形1，我们从一个点出发，将所有经过的点（包含交点）存入新的数组中，对于多边形2也是同理
对两个新数组中的相同点进行点对映射
开始对裁剪多边形1进行遍历，从任意点出发，如果改点将从多边形2的内部穿越到外部，我们改变遍历点的对象，从多边形2开始遍历，依次类推…
直到当前点被遍历过，那么之前肯定形成了一个回路，我们将当前回路绘制出来就是裁剪出的多边形。
一直重复4和5操作，直到所有点都被遍历

接下来结合图片解释一下

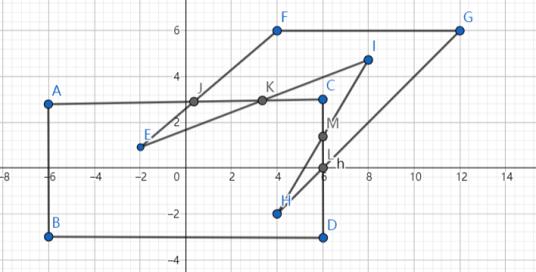
对于如下这个图，我们利用矩形裁剪凹多边形。
首先从E点出发，判断E到J是否为出点，发现不是。遍历到J点，判断JF是否是出点，发现是，这时候改变遍历的对象，通过映射关系从K点开始。判断发现KC又是出点，因此再次改变遍历对象，遍历多边形到E，发现J已经被遍历过，这时直接绘制出JKE…

程序框图

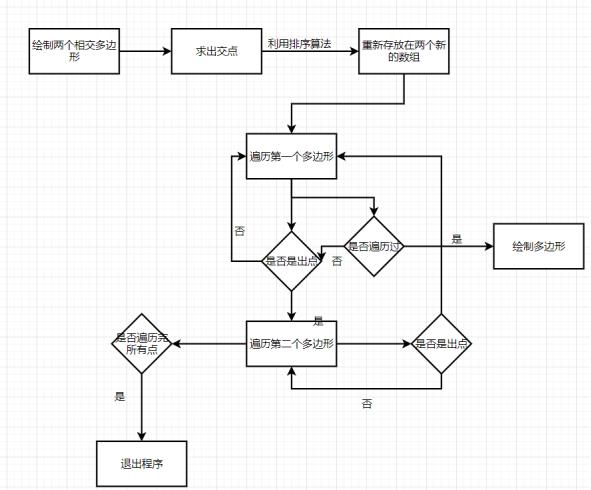
代码实现

建立窗口以及自动调整大小

void reshape(int w, int h) {
    glViewport(0, 0, w, h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective(60.0, (GLfloat)w / (GLfloat)h, 0.1, 100000.0);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    gluLookAt(0, 0, 25, 0, 0, -1, 0, 1, 0);
}
int main(int argc,char** argv) {
    glutInit(&argc, const_cast<char**>(argv));
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
    // 初始化窗口
    glutInitWindowSize(500, 500);
    glutInitWindowPosition(100, 100);
    glutCreateWindow(argv[0]);
    init();
    glutReshapeFunc(reshape);
    glutDisplayFunc(display);

    glutMainLoop();
}

建立点和线

struct Point2d {
    double x, y;
    bool operator < (const Point2d &rhs) const {
        if (x==rhs.x) return y < rhs.y;
        return x < rhs.x;
    }
};
struct Line{
    Point2d start;
    Point2d end;
};

求两条线段交点的模板，如果不存在返回-inf

inline Point2d Vector(Point2d a, Point2d b) {  //向量ab
    return{ b.x - a.x, b.y - a.y };
}
double dis2(Point2d a, Point2d b) {          //两点间的距离的平方
    return (b.x - a.x)*(b.x - a.x) + (b.y - a.y)*(b.y - a.y);
}
double cross(Point2d A, Point2d B, Point2d P) {  //向量的外积
    Point2d AB = Vector(A,B);
    Point2d AP = Vector(A,P);
    return AB.x*AP.y - AB.y*AP.x;
}
double dot(Point2d A, Point2d B, Point2d P) {     //向量的内积
    Point2d AB = Vector(A,B);
    Point2d AP = Vector(A,P);
    return AB.x*AP.x + AB.y*AP.y;
}
int dir(Point2d A, Point2d B, Point2d P) {    //点与线段方位判定
    if (cross(A, B, P) > 0)  return -1;
    else if (cross(A, B, P)<0) return 1;
    else if (dot(A, B, P) < 0) return -2;
    else if (dot(A, B, P) >= 0)
    {
        if (dis2(A, B) < dis2(A, P)) return 2;
        else return 0;
    }
    return 0;
}
double disLine(Point2d A, Point2d B, Point2d P) {   //点P到直线AB的距离
    return fabs(cross(A, B, P)) / sqrt(dis2(A, B));
}
Point2d intersection(Line u, Line v) {
    Point2d A1 = u.start;
    Point2d A2 = u.end;
    Point2d B1 = v.start;
    Point2d B2 = v.end;
    if (dir(A1, A2, B1)*dir(A1, A2, B2) <= 0 && dir(B1, B2, A1)*dir(B1, B2, A2) <= 0) {//判断有无交点
        double t = disLine(A1, A2, B1) / (disLine(A1, A2, B1) + disLine(A1, A2, B2));
        Point2d B1B2 = Vector(B1, B2);
        Point2d inter = { B1.x + B1B2.x*t, B1.y + B1B2.y*t };
        return {inter.x, inter.y};
    } else {
        return {-inf, -inf};
    }
}

求两点距离，用于排序

double dis(Point2d point1, Point2d point2) {
    return sqrt((point1.x-point2.x)*(point1.x-point2.x) + (point1.y-point2.y)*(point1.y-point2.y));
}

判断点是否落在多边形内，这里加了个误差0.001

bool isPointInsidePoly(Point2d P,const vector<Point2d>& polyVertices) {
    std::size_t vertCount = polyVertices.size();
    if (vertCount < 2)
        return false;
    Point2d tmp = P;
    for (int l = 0; l < 2; l++) {
        for (int r = 0; r < 2; r++) {
            P = tmp;
            if (l % 2) P.x += 0.001;
            else P.x -= 0.001;
            if (r % 2) P.y += 0.001;
            else P.y -= 0.001;
            bool inside = false;
            for (unsigned i = 1; i <= vertCount; ++i) {
                const Point2d &A = polyVertices[i - 1];
                const Point2d &B = polyVertices[i % vertCount];
                if ((B.y <= P.y && P.y < A.y) || (A.y <= P.y && P.y < B.y)) {
                    double t = (P.x - B.x) * (A.y - B.y) - (A.x - B.x) * (P.y - B.y);
                    if (A.y < B.y)
                        t = -t;
                    if (t < 0)
                        inside = !inside;
                }
            }
            if (inside) return inside;
        }
    }
    return false;
}

求交点以及重新放入数组

void getIntersections() {//求出所有交点以及按照顺序存放在新数组中
    int len1 = poly1.size();//求出new1
    for (int i = 0; i < len1; i++) {
        new1.push_back(poly1[i]);
        vector<Point2d> tmp;
        for (auto it2 : p2) {
            Point2d p = intersection({{poly1[i].x, poly1[i].y},{poly1[(i+1)%len1].x, poly1[(i+1)%len1].y}}, it2);
            if (p.x != -inf && p.y != -inf) tmp.push_back({p.x, p.y});
        }
        sort(tmp.begin(), tmp.end(), [&](Point2d p1, Point2d p2){
            return dis(p1, poly1[i]) < dis(p2, poly1[i]);
        });
        for (auto it : tmp) new1.push_back(it);
    }

    int len2 = poly2.size();//求出new2
    for (int i = 0; i < len2; i++) {
        new2.push_back(poly2[i]);
        vector<Point2d> tmp;
        for (auto it2 : p1) {
            Point2d p = intersection({{poly2[i].x, poly2[i].y},{poly2[(i+1)%len2].x, poly2[(i+1)%len2].y}}, it2);
            if (p.x != -inf && p.y != -inf) tmp.push_back({p.x, p.y});
        }
        sort(tmp.begin(), tmp.end(), [&](Point2d p1, Point2d p2){
            return dis(p1, poly2[i]) < dis(p2, poly2[i]);
        });
        for (auto it : tmp) new2.push_back(it);
    }
    for (int i = 0; i < new1.size(); i++) {//映射关系，给定eps为误差范围
        for (int j = 0; j < new2.size(); j++) {
            if (fabs(new1[i].x-new2[j].x)<eps&&fabs(new1[i].y-new2[j].y)<eps) {
                pos1[i] = j;
                pos2[j] = i;
            }
        }
    }
    work();
}

绘制两个多边形以及初始化操作

void prework() {
    p1.clear();
    p2.clear();
    new1.clear();
    new2.clear();
    vis1.clear();
    vis2.clear();
    pos1.clear();
    pos2.clear();
}
void display() {
    prework();//初始化
    glClear(GL_COLOR_BUFFER_BIT);
    glBegin(GL_LINES);
    glColor3f(1.0, 1.0, 1.0);
    int len1 = poly1.size();//绘制多边形
    for (int i = 0; i < len1; i++) {
        glVertex2f(poly1[i].x, poly1[i].y);
        glVertex2f(poly1[(i+1)%len1].x, poly1[(i+1)%len1].y);
        p1.push_back({{poly1[i].x, poly1[i].y}, {poly1[(i+1)%len1].x, poly1[(i+1)%len1].y}});
    }
    int len2 = poly2.size();
    for (int i = 0; i < len2; i++) {
        glVertex2f(poly2[i].x, poly2[i].y);
        glVertex2f(poly2[(i+1)%len2].x, poly2[(i+1)%len2].y);
        p2.push_back({{poly2[i].x, poly2[i].y}, {poly2[(i+1)%len2].x, poly2[(i+1)%len2].y}});
    }
    getIntersections();
    glEnd();
    glFlush();
}

最核心的代码，遍历两个多边形

void work() {
    vector<Point2d> now;//当前选择到的点
    int len1 = new1.size();
    int len2 = new2.size();
    for (int i = 0; i < new1.size(); i++) {//new1 第一个新多边形 new2第一个新多边形
        if (vis1[i]) continue;
        int ch = 1, nowpos = i;
        while (1) {
            if (ch == 1) Weiler-Atherton算法 计算机图形学多边形裁剪算法
 计算机图形学：直线段扫描转换算法
 求计算机图形学中的直线绘制函数法、DDA算法、中点法和Bresenham算法的优缺点以及比较.
 计算机图形学（三种画线算法）
 计算机图形学-二维图形生成算法
 医学图形算法开篇

Weiler-Atherton算法 计算机图形学多边形裁剪算法

目录