HDU - 4793 思维计算几何直线和圆交点

Posted 2021-12-12 hesorchen

题目

HDU 4793

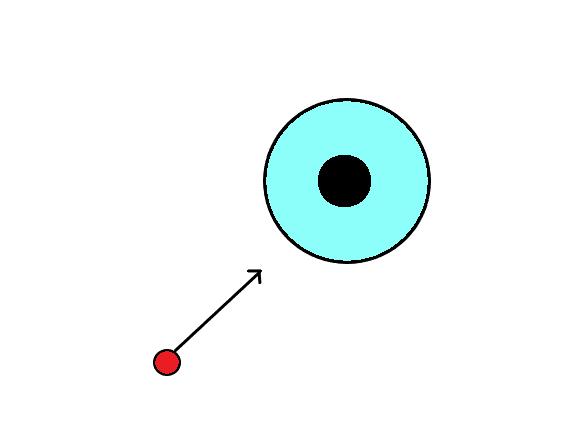
有一个圆（图中红色部分），其有一个初速度，撞到黑色部分会发生完全弹性碰撞，求红色圆在蓝色区域的时间。

题解

训练赛的题，队友给了一个关键转化，可以将蓝色、黑色圆的半径同时加上红色圆的半径，然后将红色圆缩成一个点。这样各种事件还是等价的。

转化之后就很简单了：
一、红色点不进入蓝色区域，答案为0
二、红色点进入蓝色区域但不进入黑色区域，答案为$$与蓝色区域两个交点的距离/速度$$
三、红色点进入黑色区域，可以证明的是，与黑色圆发生碰撞前后在蓝色区域的时间（路程）是一样的，求出一者乘二即可。

代码

#include <bits/stdc++.h>
using namespace std;

const double eps = 1e-6;
int sgn(double x)
{
    if (fabs(x) < eps)
        return 0;
    if (x < 0)
        return -1;
    return 1;
}
struct Point
{
    double x, y;
    Point(){};
    Point(double _x, double _y) { x = _x, y = _y; }
    Point operator*(const double &b) const { return Point{x * b, y * b}; }
    Point operator/(const double &b) const { return Point{x / b, y / b}; }
    Point operator-(const Point &b) const { return Point{x - b.x, y - b.y}; }
    Point operator+(const Point &b) const { return Point{x + b.x, y + b.y}; }
    double operator^(const Point &b) const { return x * b.y - y * b.x; }
    double operator*(const Point &b) const { return x * b.x + y * b.y; }
    bool operator==(const Point &b) const { return sgn(x - b.x) == 0 && sgn(y - b.y == 0); }
    double distance(Point p) { return hypot(x - p.x, y - p.y); }
    double len() { return hypot(x, y); }
    double len2() { return x * x + y * y; }
    Point trunc(double r)
    {
        double l = len();
        if (!sgn(l))
            return *this;
        r /= l;
        return Point(x * r, y * r);
    }
};
struct Line
{
    Point s, e;
    Line(){};
    Line(Point _s, Point _e) { s = _s, e = _e; }

    double length()
    {
        return s.distance(e);
    }
    Point lineprog(Point p)
    {
        return s + (((e - s) * ((e - s) * (p - s))) / ((e - s).len2()));
    }
    double dispointtoline(Point p)
    {
        return fabs((p - s) ^ (e - s)) / length();
    }
};
struct Circle
{
    Point p;
    double r;
    Circle(){};
    Circle(Point _p, double _r) { p = _p, r = _r; }
    int relationline(Line v)
    {
        double dst = v.dispointtoline(p);
        if (sgn(dst - r) < 0)
            return 2;
        else if (sgn(dst - r) == 0)
            return 1;
        return 0;
    }
    int pointcrossline(Line v, Point &p1, Point &p2)
    {
        if (!(*this).relationline(v))
            return 0;
        Point a = v.lineprog(p);
        double d = v.dispointtoline(p);
        d = sqrt(r * r - d * d);
        if (sgn(d) == 0)
        {
            p1 = a;
            p2 = a;
            return 1;
        }
        p1 = a + (v.e - v.s).trunc(d);
        p2 = a - (v.e - v.s).trunc(d);
        return 2;
    }
};

bool check(Point a, Point b) //同向 *
{
    return sgn(atan2(a.x, a.y) - atan2(b.x, b.y)) == 0;
}
double Rm, R, r;
Point A, V;

void solve()
{
    Rm += r, R += r;
    double speed = V.distance(Point(0, 0));
    Circle Big(Point{0, 0}, R);
    Circle Sma(Point{0, 0}, Rm);
    Line l1(A, A + V);
    if (Big.relationline(l1) <= 1)
    {
        printf("0\\n");
        return;
    }
    Point X1, X2;
    Big.pointcrossline(l1, X1, X2);
    if (!check(V, X1 - A))
    {
        printf("0\\n");
        return;
    }

    // 保证和大圆相交 有两个交点X1 X2
    if (Sma.relationline(l1) <= 1)
    {
        printf("%.6f\\n", X1.distance(X2) / speed);
    }
    else
    {
        Point X3, X4;
        Sma.pointcrossline(l1, X3, X4);
        if (X3.distance(A) > X4.distance(A))
            swap(X3, X4);
        if (X1.distance(A) > X2.distance(A))
            swap(X1, X2);
        printf("%.6f\\n", 2.0 * X3.distance(X1) / speed);
    }
}

int main()
{
    while (~scanf("%lf %lf %lf %lf %lf %lf %lf", &Rm, &R, &r, &A.x, &A.y, &V.x, &V.y))
        solve();
    return 0;
}