优先级队列(堆)
Posted Escapesisi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优先级队列(堆)相关的知识,希望对你有一定的参考价值。
优先级队列(堆)
优先级队列(PriorityQueue)
优先级队列的概念
我们都知道队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时可能需要优先级高的元素出队列,此时队列就显得不合适了。因此我们引入优先级队列(PriorityQueue)
该数据结构应提供两个基本操作:
1.返回最高优先级对象
2.添加新的对象
在集合框架中所处的位置
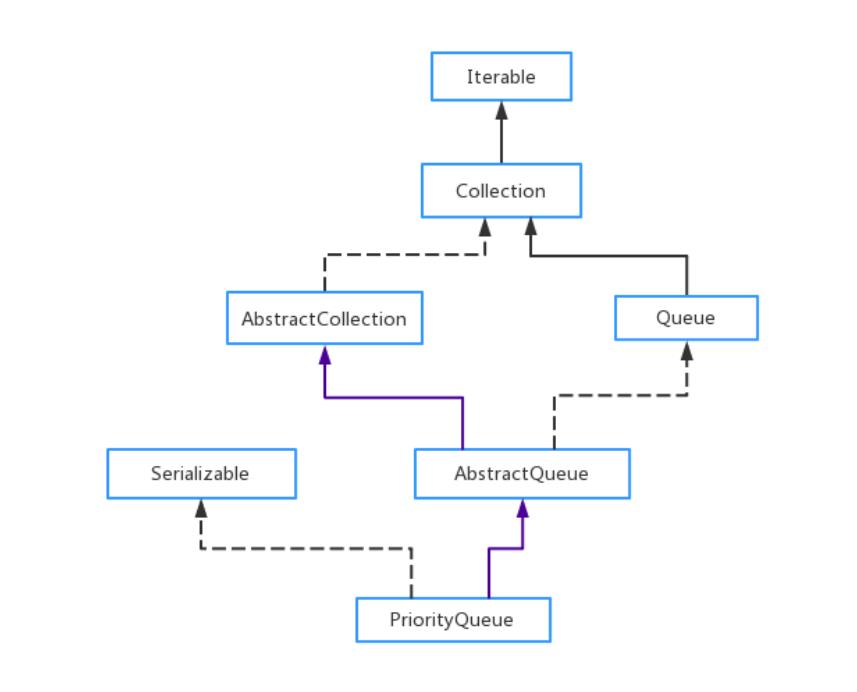
java集合中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的
优先级队列的特性
1.注意的点
1.使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue;
2.PriorityQueue中放置元素必须能够比较大小,不能插入无法比较大小的对象,否则会抛出异常
3.不能插入null对象,否则会抛出NullPointerException
4.没有容量限制,可以插入任意多个元素,其内部可以自动扩容
当容量小于64时,按照 oldCapacity 的 2 倍方式扩容;
当容量大于等于64,按照 oldCapacity 的1.5倍方式扩容;
当容量超过 MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE 进行扩容;
jdk1.8 中,PriorityQueue的扩容方式:
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {
int oldCapacity = queue.length;
int newCapacity = oldCapacity + ((oldCapacity < 64) ? (oldCapacity + 2): (oldCapacity >> 1));
if (newCapacity - MAX_ARRAY_SIZE > 0) {
newCapacity = hugeCapacity(minCapacity);
}
queue = Arrays.copyOf(queue,newCapacity);
}
5.插入和删除元素的时间复杂度为O(log2N)
6.PriorityQueue底层使用了堆数据结构
7.PriorityQueue默认情况下是小堆——即每次获取到的元素都是最小的
如果想要创建大堆,则需要构造比较器——实质:实现 Comparator 接口,重写该接口中的 compare 方法
大堆创建代码如下:
//用户自己定义的比较器:直接实现Comparator接口,然后重写该接口中compare方法即可
import java.util.Comparator;
public class IntCmp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1; //o1-o2就是小堆
}}
import java.util.PriorityQueue;
public class TestPriorityQueue {
public static void main(String[] args) {
PriorityQueue<Integer> q = new PriorityQueue<>(new IntCmp());
q.offer(1);
q.offer(2);
q.offer(5);
q.offer(3);
System.out.println(q.peek()); //5
}
}
也可以写成这样:
import java.util.PriorityQueue;
import java.util.Comparator;
public class TestPriorityQueue {
public static void main(String[] args) {
PriorityQueue<Integer> q = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1; //o1-o2就是小堆
}
});
q.offer(1);
q.offer(2);
q.offer(5);
q.offer(3);
System.out.println(q.peek()); //5
}
}
2.三种构造方法
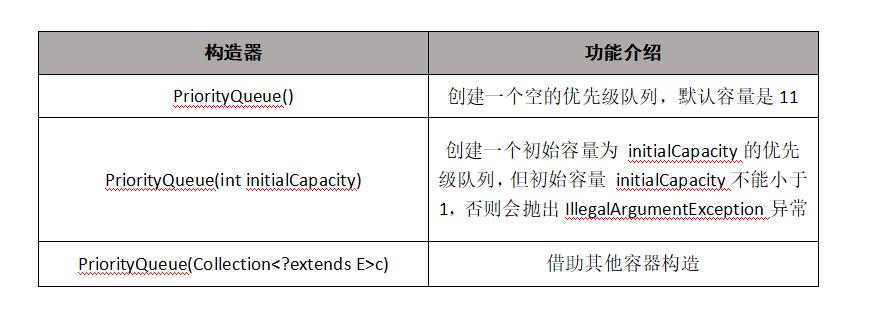
3.插入/删除/获取优先级最高的元素
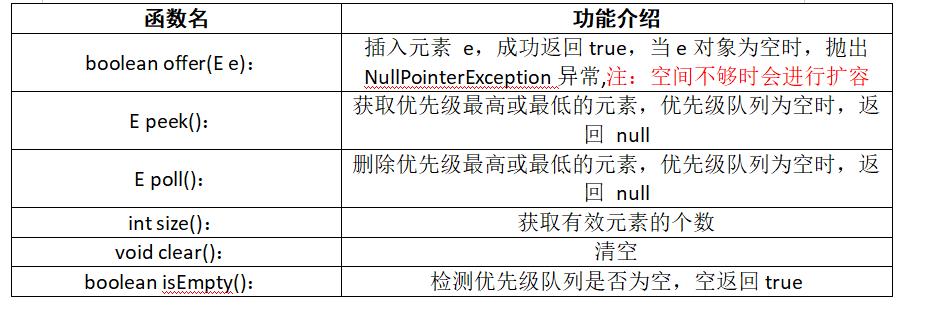
测试代码如下:
import java.util.PriorityQueue;
public class TestPriorityQueue {
public static void method(){
int[] arr = {4,1,9,2,3,6,7,8,5};
PriorityQueue<Integer> q=new PriorityQueue<>(arr.length);
for(int e:arr) {
q.offer(e);
}
System.out.println(q.size()); //9
System.out.println(q.peek()); //1
q.poll();
q.poll();
System.out.println(q.size()); //7
System.out.println(q.peek()); //3
q.clear();
if(q.isEmpty()){
System.out.println("优先级队列为空");
}else{
System.out.println("优先级队列不为空");
}
}
public static void main(String[] args) {
method();
}
}
优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆的数据结构,而堆实际就是在完全二叉树的基础上进行一些元素的调整
1.堆的概念
n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。
(ki ≤ k2i且ki ≤ k2i+1)或者(ki ≥ k2i且ki ≥ k2i+1),若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)
(摘自百度百科)
总之:将根节点最大的堆叫大堆,将根节点最小的堆叫小堆
- 堆中某个结点的值总是不大于或不小于其父结点的值
- 堆总是一棵完全二叉树。

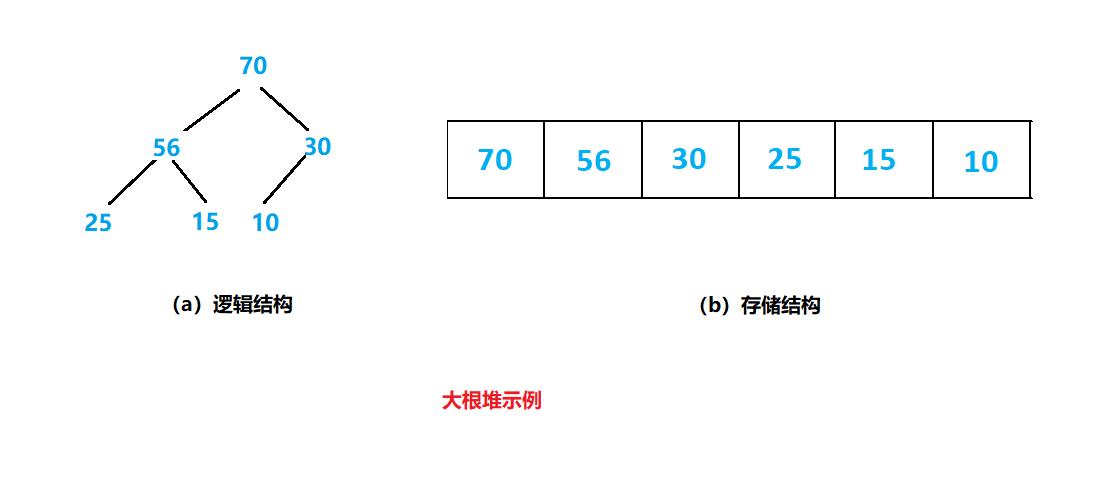
2.堆的存储方式
从堆的概念可知,堆是一颗完全二叉树,因此可以层序的规则采用顺序的方式来高效存储
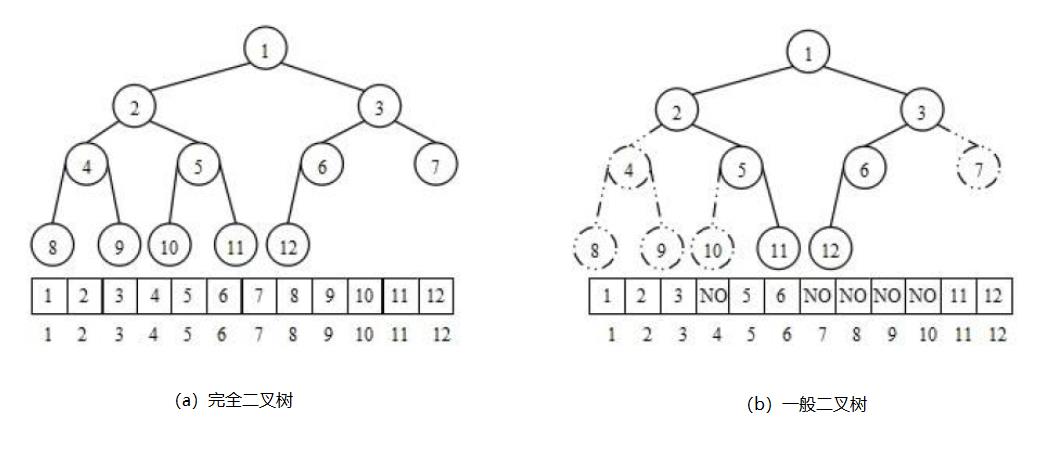
注:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空结点,就会导致空间利用率比较低
2.堆的创建
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如果将其创建成堆呢?
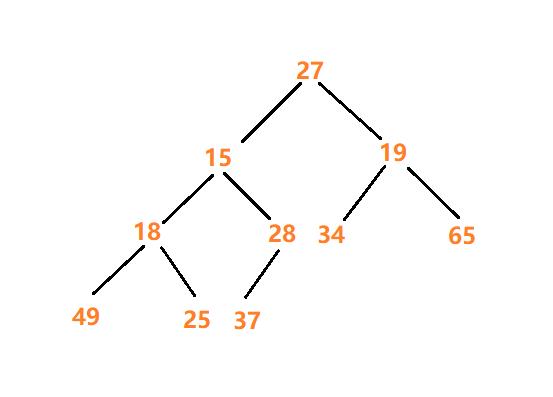
不难发现:根结点的左右子树均已满足堆的性质(除根结点外,其余结点均是小于其孩子结点的),
如下图所示:
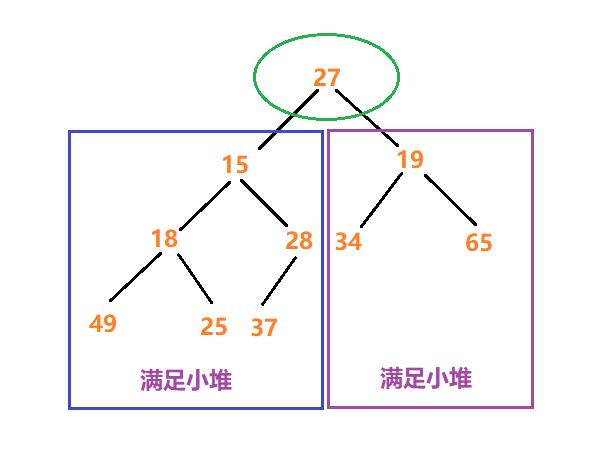
因此,只需要将根结点向下调整到合适位置即可创建一个小堆;
向下调整步骤:
- a.让 parent 标记需要调整的结点,child 标记其左孩子的结点( 注意:parent如果有孩子一定先是有左孩子)
- b.如果左孩子存在时,即:(child<size)就进行以下操作,直到parent的左孩子不存在:
(1)parent右孩子是否存在,存在将左右孩子进行比较,让child 标记出找出的较小的那个孩子;
(2)将parent与较小的那个孩子进行比较,当 parent>child
标记的孩子时,就进行交换;但交换可能就会导致下面子树不满足堆的特性,因此,需要更新变量(parent=child,child=parent*2+1),继续
b 操作,
注意:
在将某结点往下调整时,必须保证该结点的左右子树均满足堆的特性,才能使用;
代码如下:
public void shiftDown(int[] array){
int parent=0;
int child=2*parent+1; //child来标记左孩子
int size=array.length;
while(child<size){
// 右孩子存在时,找左右孩子中较小的孩子,用child进行标记
if(child+1 < size && array[child+1] < array[child]){
child += 1;
}
// 如果双亲比其最小的孩子还小,说明该结构已经满足堆的特性了
if (array[parent] <= array[child]) {
break;
}else{
//将双亲与较小的孩子进行交换
int temp=array[parent];
array[parent]=array[child];
array[child]=temp;
// 当parent中大的元素往下移动时,可能会造成子树不满足堆的性质,因此需要继续向下调整
parent = child;
child = parent * 2 + 1;
}
}
}
public static void main(String[] args) {
int[] array={27,15,19,18,28,34,65,49,25,37};
shiftDown(array);
}
}
对于以上属于特殊情况,如遇到左右子树不满足堆特性的情况该如何处理?
任意序列建堆:
- (1)找到当前树中的倒数第一个非叶子结点,该结点也是最后一个结点的双亲所在的位置,而最后一个结点的位置下标为 size-1;
其双亲的下标为:((size-1)-1)/2; - (2)从该非叶子结点开始往回倒,直到根的位置,遇到一个结点,就以该结点为二叉树进行向下调整;
代码如下:
public static void createHeap(int[] array) {
// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根结点,遇到一个结点,应用向下调整
int root = ((array.length-2)>>1);
for (; root >= 0; root--) {
shiftDown(array,root);
}
}
3.堆的插入
堆的插入有两个步骤:
(1)先将元素放入底层空间中(注意:空间不够时需要扩容)
(2)将最后新插入的结点向上调整,直到满足堆的性质
public void offer(int e){
array[size]=e;
size++;
//将插入的新元素向上调整
shiftUp(array,size-1);
}
3.堆的删除
(1)将堆顶元素与堆中最后一个元素进行交换
(2)将堆中有效数据的个数减少一个
(3) 对堆顶元素进行向下调整
public Integer poll(){
int ret=array[0];
//将堆顶元素与最后一个元素交换
array[0]=array[size-1];
//堆中有效元素个数减少一个
size--;
//将堆顶元素使用向下调整到合适位置
shiftDown(array,size,0);
return ret;
}
4.获取堆顶元素
public int peek(){
return array[0];
}
以上就是本次的全部内容~~
以上是关于优先级队列(堆)的主要内容,如果未能解决你的问题,请参考以下文章