Verma constraint简介
Posted Jie Qiao
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Verma constraint简介相关的知识，希望对你有一定的参考价值。
一个神奇的现象
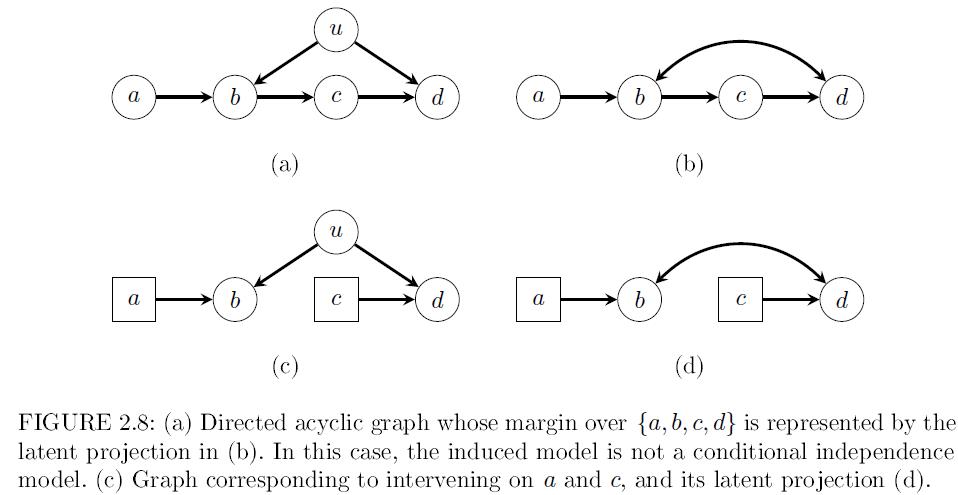
如图(a)所示，在这个结构中，U是隐变量，对于这样的一个分布：
∑ b P ( d ∣ a , b , c ) P ( b ∣ a ) = f ( c , d ) \\sum _{b} P( d|a,b,c) P( b|a) =f( c,d) b∑P(d∣a,b,c)P(b∣a)=f(c,d)
他不是一个关于a的函数！我们发现在某个神奇的边缘分布中，产生了一种额外的独立性！而我们知道独立性是一种非常有效的研究因果结构的方法，得到的独立性越多，所圈定的因果结构的范围就越小。那么这些“多出来的”独立性是能够帮助我们识别出更多的因果结构的。
那么这种现象是怎么来的呢？接下来就要介绍Verma constraint
Verma constraint
我们先看看上面的那个分布是怎么来的，首先对于边缘分布 p ( a , b , c , d ) \\displaystyle p( a,b,c,d) p(a,b,c,d)，可以如下展开：
p ( a , b , c , d ) = ∑ u p ( u ) ⋅ p ( a ) ⋅ p ( b ∣ a , u ) ⋅ p ( c ∣ b ) ⋅ p ( d ∣ c , u ) = p ( a ) ⋅ p ( c ∣ b ) ⋅ ∑ u p ( u ) ⋅ p ( b ∣ a , u ) ⋅ p ( d ∣ c , u ) ≡ q a ( a ) ⋅ q c ( c ∣ b ) ⋅ q { b , d } ( b , d ∣ a , c ) . (1) \\begin{aligned} & p( a,b,c,d)\\\\ & =\\sum _{u} p( u) \\cdot p( a) \\cdot p( b\\mid a,u) \\cdot p( c\\mid b) \\cdot p( d\\mid c,u)\\\\ & =p( a) \\cdot p( c\\mid b) \\cdot \\sum _{u} p( u) \\cdot p( b\\mid a,u) \\cdot p( d\\mid c,u)\\\\ & \\equiv q_{a}( a) \\cdot q_{c}( c\\mid b) \\cdot q_{\\{b,d\\}}( b,d\\mid a,c) . \\end{aligned} \\tag{1} p(a,b,c,d)=u∑p(u)⋅p(a)⋅p(b∣a,u)⋅p(c∣b)⋅p(d∣c,u)=p(a)⋅p(c∣b)⋅u∑p(u)⋅p(b∣a,u)⋅p(d∣c,u)≡qa(a)⋅qc(c∣b)⋅q{b,d}(b,d∣a,c).(1)
可以看到，因为有隐变量的存在，所以这个边缘分布可以依照隐变量的积分，划分成3块(districts), { a } , { c } , { b , d } \\displaystyle \\{a\\} ,\\{c\\} ,\\{b,d\\} {a},{c},{b,d}，也有的地方叫C-components。那么，显然前两块跟p是一致的，即 p ( a ) = q a ( a ) \\displaystyle p( a) =q_{a}( a) p(a)=qa(a)， p ( c ∣ b ) = q c ( c ∣ b ) \\displaystyle p( c\\mid b) =q_{c}( c\\mid b) p(c∣b)=qc(c∣b)，那么最后一块是什么呢？显然，我们把全概率除以前面两项就是q了，于是
q { b , d } ( b , d ∣ a , c ) = p ( a , b , c , d ) p ( a ) p ( c ∣ b ) = p ( a , b , c , d ) p ( a ) p ( c ∣ a , b ) = p ( a ) p ( b , c , d ∣ a ) p ( a ) p ( c ∣ a , b ) = p ( a ) p ( d ∣ a , b , c ) p ( b , c ∣ a ) p ( a ) p ( c ∣ a , b ) = p ( a ) p ( d ∣ a , b , c ) p ( c ∣ a , b ) p ( b ∣ a ) p ( a ) p ( c ∣ a , b ) = p ( d ∣ a , b , c ) p ( b ∣ a ) \\begin{aligned} q_{\\{b,d\\}}( b,d\\mid a,c) & =\\frac{p( a,b,c,d)}{p( a) p( c\\mid b)}\\\\ & =\\frac{p( a,b,c,d)}{p( a) p( c\\mid a,b)}\\\\ & =\\frac{p( a) p( b,c,d|a)}{p( a) p( c\\mid a,b)}\\\\ & =\\frac{p( a) p( d|a,b,c) p( b,c|a)}{p( a) p( c\\mid a,b)}\\\\ & =\\frac{p( a) p( d|a,b,c) p( c|a,b) p( b|a)}{p( a) p( c\\mid a,b)}\\\\ & =p( d|a,b,c) p( b|a) \\end{aligned} q{b,d}(b,d∣a,c)=p(a)p(c∣b)p(a,b,c,d)=p(a)p(c∣a,b)p(a,b,c,d)=p(a)p(c∣a,b)p(a)p(b,c,d∣a)=p(a)p(c∣a,b)p(a)p(d∣a,b,c)p(b,c∣a)=p(a)p(c∣a,b)p(a)p(d∣a,b,c)p(c∣a,b)p(b∣a)=p(d∣a,b,c)p(b∣a)
其中第二个等号是因为 p ( c ∣ b ) = p ( c ∣ a , b ) \\displaystyle p( c\\mid b) =p( c\\mid a,b) p(c∣b)=p(c∣a,b)。显然这个分布就是我们在上文提到的那个神奇的现象的分布，那这个分布是什么东西？
首先这个分布显然与
p
(
b
,
d
∣
a
,
c
)
\\displaystyle p( b,d|a,c)
p(b,d∣a,c)不是同一个，实际上，这是一个干预后的分布！即
q
{
b
,
d
}
(
b
,
d
∣
a
,
c
)
=
p
(
b
,
d
∣
d
o
(
a
,
c
)
)
\\displaystyle q_{\\{b,d\\}}( b,d\\mid a,c) =p( b,d|do( a,c))
q{b,d}(b,d∣a,c)=p(b,d∣do(a,c))，这个分布的概率是对应着图©的！为什么呢？因为干预后的分布发生的概率为1，即
p
(
d
o
(
a
)
)
=
p
(
d
o
(
c
)
∣
b
)
=
1
以上是关于Verma constraint简介的主要内容，如果未能解决你的问题，请参考以下文章 Oracle的ORA-02292报错：违反完整性约束，已找到子记录 升级到 5.4 后在 Laravel BrowserKit 包中找不到 PHPUnit\Framework\Constraint\Constraint oracle inner join | outer join | full join | add constraint | drop constraint | disable constraint |