刷题日记Day2 | 构造二叉树

Posted 2021-12-11 结构化思维wz

把题目的要求细化，搞清楚根节点应该做什么，然后剩下的事情抛给前/中/后序的遍历框架就行了，我们千万不要跳进递归的细节里，你的脑袋才能压几个栈呀。

文章目录

• • 654.最大二叉树
  • 105.根据前序和中序序列构造二叉树
  • 106.根据中序和后续遍历构造二叉树

654.最大二叉树

分析：
1.根节点要做什么？？
把自己构建出来。
2.具体做什么？？
遍历数组把找到最大值 maxVal，把根节点 root 做出来，然后对 maxVal 左边的数组和右边的数组进行递归调用，作为 root 的左右子树。
解题思路：

TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) {
    // 找到数组中的最大值
    TreeNode root = new TreeNode(6);
    // 递归调用构造左右子树
    root.left = constructMaximumBinaryTree([3,2,1]);
    root.right = constructMaximumBinaryTree([0,5]);
    return root;
}

解答：

/* 主函数 */
TreeNode constructMaximumBinaryTree(int[] nums) {
    return build(nums, 0, nums.length - 1);
}

/* 将 nums[lo..hi] 构造成符合条件的树，返回根节点 */
TreeNode build(int[] nums, int lo, int hi) {
    // base case
    if (lo > hi) {
        return null;
    }

    // 找到数组中的最大值和对应的索引
    int index = -1, maxVal = Integer.MIN_VALUE;
    for (int i = lo; i <= hi; i++) {
        if (maxVal < nums[i]) {
            index = i;
            maxVal = nums[i];
        }
    }

    TreeNode root = new TreeNode(maxVal);
    // 递归调用构造左右子树
    root.left = build(nums, lo, index - 1);
    root.right = build(nums, index + 1, hi);
    
    return root;
}

---

105.根据前序和中序序列构造二叉树

⭐️重点题型标注！

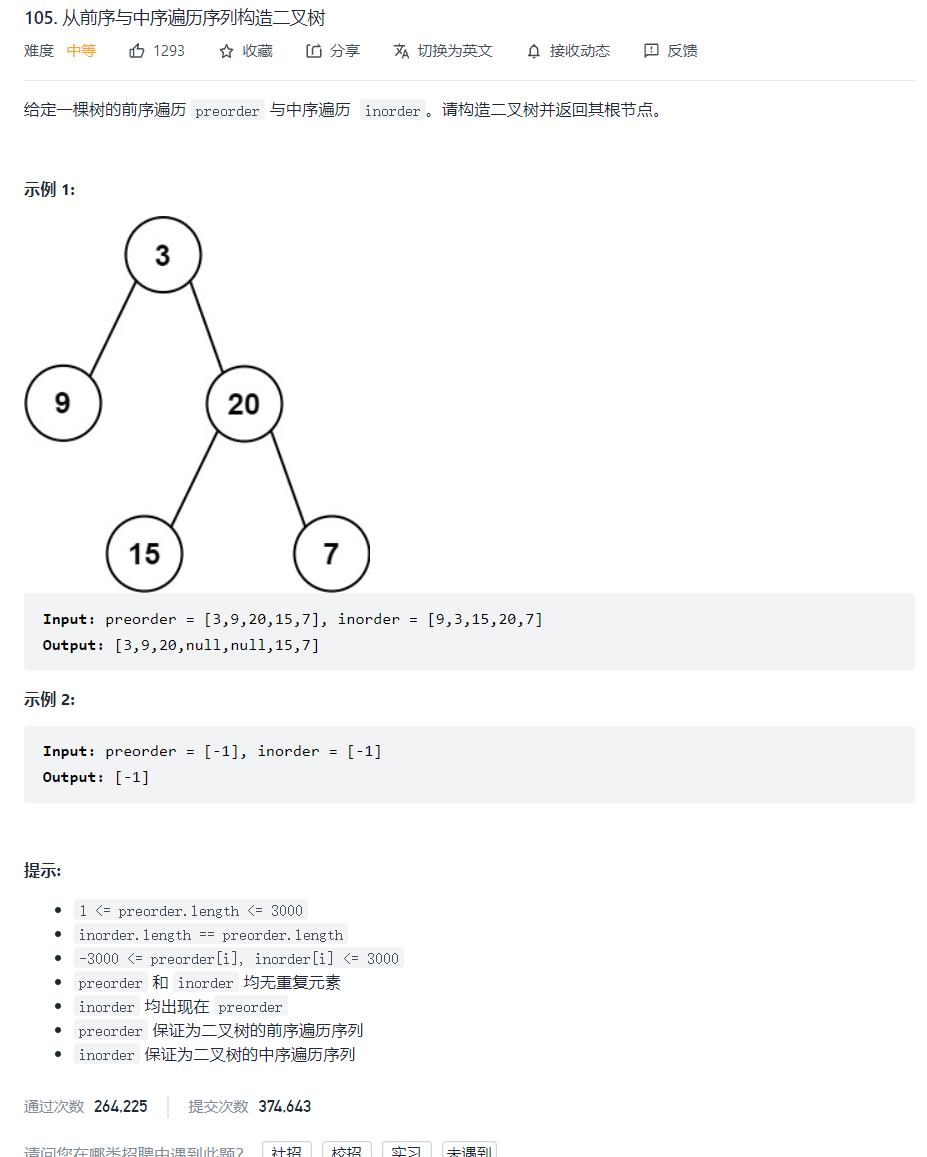
分析：
想办法确定根节点的值，把根节点做出来，然后递归构造左右子树即可。
如何找到根节点？？

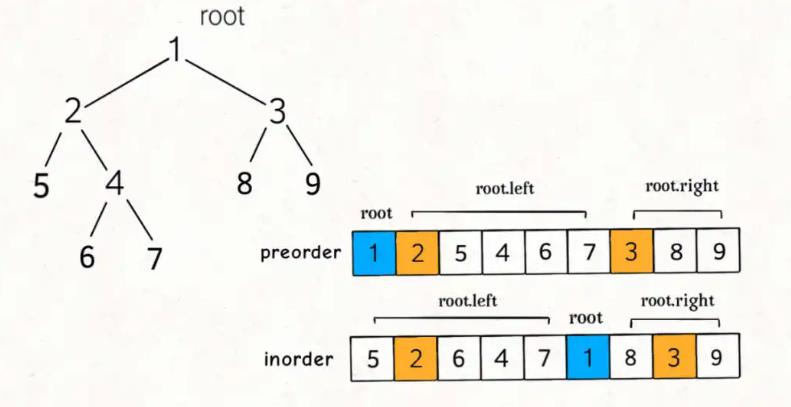
前序遍历的第一个值preorder[0]就是根节点的值，关键在于如何通过根节点的值，将preorder和postorder数组划分成两半，构造根节点的左右子树？

根据思路写出对应的代码为：

/* 主函数 */
TreeNode buildTree(int[] preorder, int[] inorder) {
    return build(preorder, 0, preorder.length - 1,
                 inorder, 0, inorder.length - 1);
}

/* 
   若前序遍历数组为 preorder[preStart..preEnd]，
   后续遍历数组为 postorder[postStart..postEnd]，
   构造二叉树，返回该二叉树的根节点 
*/
TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {
    // root 节点对应的值就是前序遍历数组的第一个元素
    int rootVal = preorder[preStart];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }

    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(preorder, ?, ?,
                      inorder, ?, ?);

    root.right = build(preorder, ?, ?,
                       inorder, ?, ?);
    return root;
}

得到构造左右子树的代码：

解答：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

TreeNode buildTree(int[] preorder, int[] inorder) {
    return build(preorder, 0, preorder.length - 1,
                 inorder, 0, inorder.length - 1);
}
/* 
   若前序遍历数组为 preorder[preStart..preEnd]，
   后续遍历数组为 postorder[postStart..postEnd]，
   构造二叉树，返回该二叉树的根节点 
*/
 TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {

    if (preStart > preEnd) {
        return null;
    }

    // root 节点对应的值就是前序遍历数组的第一个元素
    int rootVal = preorder[preStart];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }

    int leftSize = index - inStart;

    // 先构造出当前根节点
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(preorder, preStart + 1, preStart + leftSize,
                      inorder, inStart, index - 1);

    root.right = build(preorder, preStart + leftSize + 1, preEnd,
                       inorder, index + 1, inEnd);
    return root;
}
}

---

106.根据中序和后续遍历构造二叉树

分析：
有了上一题的基础，发现只要画图发现左右子树的起止点就可以了。



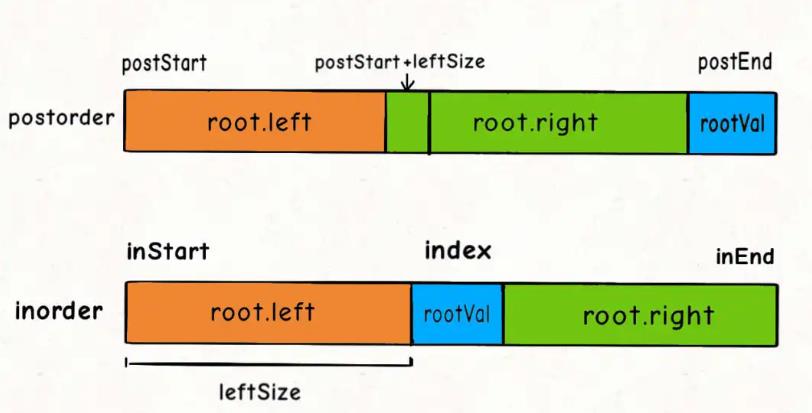
代码实现：

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return build(inorder,0,inorder.length-1,
                postorder,0,postorder.length-1);
    }
    /**构建二叉树 */
    TreeNode build(int[] inorder, int inStart, int inEnd,
               int[] postorder, int postStart, int postEnd) {

    if (inStart > inEnd) {
        return null;
    }
    // root 节点对应的值就是后序遍历数组的最后一个元素
    int rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }
    // 左子树的节点个数
    int leftSize = index - inStart;
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(inorder, inStart, index - 1,
                        postorder, postStart, postStart + leftSize - 1);

    root.right = build(inorder, index + 1, inEnd,
                        postorder, postStart + leftSize, postEnd - 1);
    return root;
}
}

---