二叉树的前序遍历中序遍历后序遍历

Posted 2021-12-11 yangbocsu

绝对要收藏【数据结构之树】

• 一、基础概念
• 二、前序遍历
• • 2.1 递归参考代码
  • 2.2 非递归参考代码
• 三、中序遍历
• • 3.1 递归参考代码
  • 3.2 非递归参考代码
• 四、后序遍历

一、基础概念

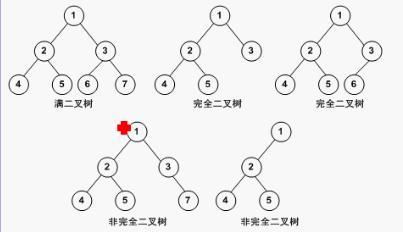
• 树 ：由n个有限节点组成的一个具有层次关系的集合；
• 根节点 ：没有父节点的节点；

二、前序遍历

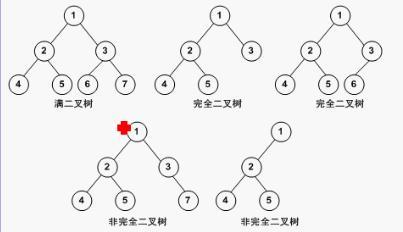
• 遍历顺序：根节点→左节点→右节点
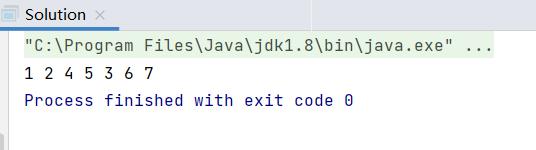
• 满二叉树遍历顺序：1→2→4→5→3→6→7

2.1 递归参考代码

package com.work;
import java.util.Stack;
/**
 * @author: By yangbocsu
 * @date: 2021-11-11
 * @description: 二叉树前序遍历
 */
public class Solution {
    public static void main(String[] args)
    {
        TreeNode root = new TreeNode(1);
        TreeNode n1 = new TreeNode(2);
        TreeNode n2 = new TreeNode(3);
        TreeNode n3 = new TreeNode(4);
        TreeNode n4 = new TreeNode(5);
        TreeNode n5 = new TreeNode(6);
        TreeNode n6 = new TreeNode(7);

        root.left = n1;
        root.right = n2;

        n1.left = n3;
        n1.right = n4;

        n2.left = n5;
        n2.right = n6;

        preOrder(root);
    }

    public static void preOrder(TreeNode tree)//前序遍历 递归法
    {
        if (tree == null)
            return;
        System.out.print(tree.val + " ");
        preOrder(tree.left);
        preOrder(tree.right);
    }

    //Definition for a binary tree node.
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val)
        {
            this.val = val;
        }
        TreeNode(int val, TreeNode left, TreeNode right)
        {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

}

2.2 非递归参考代码

package com.work;
import java.util.Stack;
/**
 * @author: By yangbocsu
 * @date: 2021-11-11
 * @description: 前序遍历 非递归法
 */
public class Solution {
    public static void main(String[] args)
    {
        TreeNode root = new TreeNode(1);
        TreeNode n1 = new TreeNode(2);
        TreeNode n2 = new TreeNode(3);
        TreeNode n3 = new TreeNode(4);
        TreeNode n4 = new TreeNode(5);
        TreeNode n5 = new TreeNode(6);
        TreeNode n6 = new TreeNode(7);

        root.left = n1;
        root.right = n2;

        n1.left = n3;
        n1.right = n4;

        n2.left = n5;
        n2.right = n6;

        preOrder(root);
    }

    //前序遍历 非递归法
    public static void preOrder(TreeNode tree)
    {
        if (tree == null)
            return;
        Stack<TreeNode> q1 = new Stack<>();
        q1.push(tree);//压栈    到这里tree 肯定非空
        while (!q1.empty())
        {
            TreeNode t1 = q1.pop();//出栈
            System.out.print(t1.val+" ");
            //前序遍历时   先压右子树再压左子树，弹出来的时候就是，先先左后右
            if (t1.right != null)
            {
                q1.push(t1.right);
            }
            if (t1.left != null)
            {
                q1.push(t1.left);
            }
        }
    }

    //Definition for a binary tree node.
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val)
        {
            this.val = val;
        }
        TreeNode(int val, TreeNode left, TreeNode right)
        {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

}

三、中序遍历

• 遍历顺序：左节点→根节点→右节点
• 满二叉树遍历顺序：4→2→5→1→6→3→7
• 

3.1 递归参考代码

package com.work;
import java.util.Stack;
/**
 * @author: By yangbocsu
 * @date: 2021-11-11
 * @description: 二叉树中序遍历 递归法
 */
public class Solution
{
    public static void main(String[] args)
    {
        TreeNode root = new TreeNode(1);
        TreeNode n1 = new TreeNode(2);
        TreeNode n2 = new TreeNode(3);
        TreeNode n3 = new TreeNode(4);
        TreeNode n4 = new TreeNode(5);
        TreeNode n5 = new TreeNode(6);
        TreeNode n6 = new TreeNode(7);

        root.left = n1;
        root.right = n2;

        n1.left = n3;
        n1.right = n4;

        n2.left = n5;
        n2.right = n6;

        inOrderTraversal(root);
    }

    public static void inOrderTraversal(TreeNode tree)//中序遍历 递归法
    {
        if (tree == null)
            return;
        // 中序遍历  左节点 → 根节点 → 右节点
        inOrderTraversal(tree.left);
        System.out.print(tree.val + " ");
        inOrderTraversal(tree.right);
    }

    //Definition for a binary tree node.
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val)
        {
            this.val = val;
        }
        TreeNode(int val, TreeNode left, TreeNode right)
        {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

}

3.2 非递归参考代码

package com.work;
import java.util.Stack;
/**
 * @author: By yangbocsu
 * @date: 2021-11-11
 * @description: 前序遍历 非递归法
 */
public class Solution {
    public static void main(String[] args)
    {
        TreeNode root = new TreeNode(1);
        TreeNode n1 = new TreeNode(2);
        TreeNode n2 = new TreeNode(3);
        TreeNode n3 = new TreeNode(4);
        TreeNode n4 = new TreeNode(5);
        TreeNode n5 = new TreeNode(6);
        TreeNode n6 = new TreeNode(7);

        root.left = n1;
        root.right = n2;

        n1.left = n3;
        n1.right = n4;

        n2.left = n5;
        n2.right = n6;

        preOrder(root);
    }

    //非递归法  中序遍历  左节点 → 根节点 → 右节点
    public static void preOrder(TreeNode tree)
    {
        Stack<TreeNode> q1 = new Stack<>();
        while (tree !=null || !q1.isEmpty())
        {
            while (tree !=null)
            {
                q1.push(tree);
                tree = tree.left;
            }
            if (!q1.isEmpty())
            {
                tree = q1.pop();
                System.out.print(tree.val+" ");
                tree = tree.right;
            }
        }
    }

    //Definition for a binary tree node.
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val)
        {
            this.val = val;
        }
        TreeNode(int val, TreeNode left, TreeNode right)
        {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

}

四、后序遍历

• 遍历顺序：左节点→右节点→根节点
• 满二叉树遍历顺序：4→2→5→1→6→3→7
• 

2.1 递归参考代码
2.2 非递归参考代码