重复事件（表现形态：活跃留存复购）建模（生存分析）的案例学习笔记

Posted 2021-12-11 悟乙己

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了重复事件（表现形态：活跃留存复购）建模（生存分析）的案例学习笔记相关的知识，希望对你有一定的参考价值。

医学中，重复事件较多，那么放在一些大场景中就会有，用户重复点击/浏览（留存），重复购买（复购）这些场景。
最近也看到一些类似的case就简单整理一下：

笔者之前生存分析的文章：

文章目录

1 腾讯看点：扩展Cox模型在用户留存与复购建模中的应用
2 用户活跃度：快手的生存分析 for 重复事件
- 2.1 快手生存分析内容快速回顾
- 2.2 指标阈值确定下腾讯看点与快手的差别
3 淘系：用户复购策略的原理与实现 Buy It Again

1 腾讯看点：扩展Cox模型在用户留存与复购建模中的应用

腾讯看点和快手在一些推断分析中，有非常多好的应用，比如现在的这篇：扩展Cox模型在用户留存与复购建模中的应用
解决的核心点，是留存率的计算：N日留存分类器 -> cox模型

1.1 N日留存分类器的弊端：

这里说的N日留存分类器对象是个人级别的留存概率，而在做Cohort Analysis的留存是一个群组的概念：用户增长——Cohort Analysis 留存分析（三）

N日留存分类器属于截面数据分析，得到的结果是单纯的不同用户之间差异的结果，而当我们关注用户粘性的提升时，关注的是同群用户在时序之间的差异（没有考虑动态时序）
留存率掩盖了关于用户粘性的深层信息。举个例子，下图为2个虚构的产品的用户活跃记录（没有充分理解数据特征）：

1.2 cox模型的选择

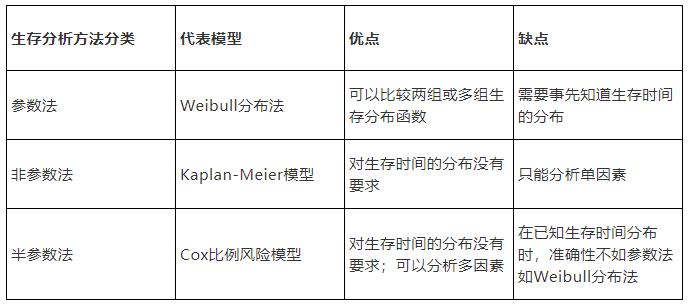
在本场景中，用户活跃时间的分布不符合某一特定分布，因此不宜使用参数法；同时，影响用户活跃的因素是多种的而非单一的，因此非参数法也不适用；半参数法是唯一适合的选择。

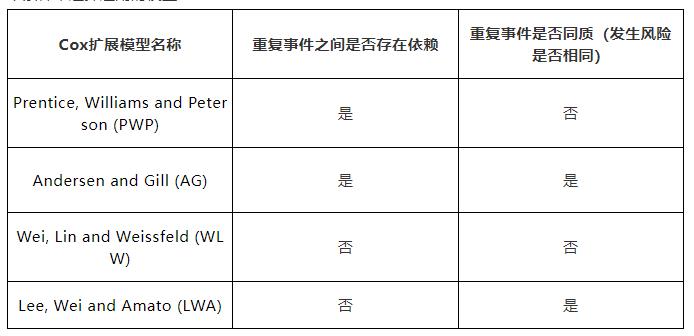
Cox模型有以下四种主要的扩展模型。基于它们的不同特性，我们可以用2个条件来选择适用的模型：

在用户粘性识别场景中，用户来访app获得的体验可能影响下一次来访的可能性，因此重复事件存在前后依赖性；另外由于app包含多样功能，用户每次来访未必是基于同样的原因，因此重复事件并不同质。

基于以上2个条件，PWP 模型在四种扩展模型中最为适合。PWP 模型通过分层来分析有序重复事件，因此不要求重复事件是同质的，不同的事件可以有不同的基线风险。

在本场景中，除了用户后续活跃的概率，还需考虑后续活跃的时间间隔，时间间隔越短意味着用户粘性越强。因此，PWP-GT 模型是最合适的选择。

1.3 COX模型PWP-GT的解读

1.3.1 示例

模拟的数据为：

重复事件模拟数据：

样本数量图片为100，观测结束时间为20；（相当于对100个用户进行观测，观测的时间长度为20）
3个协变量X.1、X.2、X.3分别服从概率p为0.6的二项分布；（即每一个用户都有X.1、X.2、X.3 这3个属性作为特征，3个变量均为0/1变量，由p=0.6的二项分布生成）
3个协变量对应的系数分别为-2、1、0.5；

重复事件建模结果如下，3个协变量X.1、X.2、X.3的exp(coef) 分别为0.58、1.27、1.13（即hazard ratio）。小于1的exp(coef) 说明该变量的增加会降低事件发生的概率，反之，大于1的exp(coef) 说明该变量的增加会增加事件发生的概率。

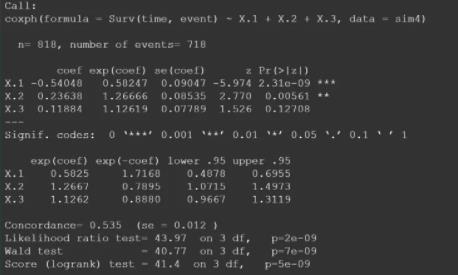
协变量X.1的hazard ratio为0.58，意为X.1为1的样本在任意时刻发生事件的概率是X.1为0的样本的0.58倍，即X.1为1相较0会降低事件发生的概率42%。
协变量X.2的hazard ratio为1.27，意为X.2为1的样本在任意时刻发生事件的概率是X.2为0的样本的1.27倍，即X.2为1相较0会增加事件发生的概率27%。
协变量X.3的hazard ratio为1.13，意为X.3为1的样本在任意时刻发生事件的概率是X.3为0的样本的1.13倍，即X.3为1相较0会增加事件发生的概率13%。
即协变量X.1、X.2、X.3，各自为1相较为0，对任意时刻事件发生概率的影响分别为-42%、27%、13%（以X.2为基准数进行等比例转换后为-1.6、1、0.5），与数据生成的实际协变量系数-2、1、0.5，在影响的方向、影响量级的比例上的一致性较高。

1.3.2 PWP-GT 重复事件建模在看点业务中的实际应用

这里通过离散回归的方式，来鉴定某个指标哪个分数区间更好

由于用户的活跃是重复事件，这里用到了重复事件建模；为了聚焦多次事件的发生间隔，选用PWP-GT模型。数据的基本结构如下表：

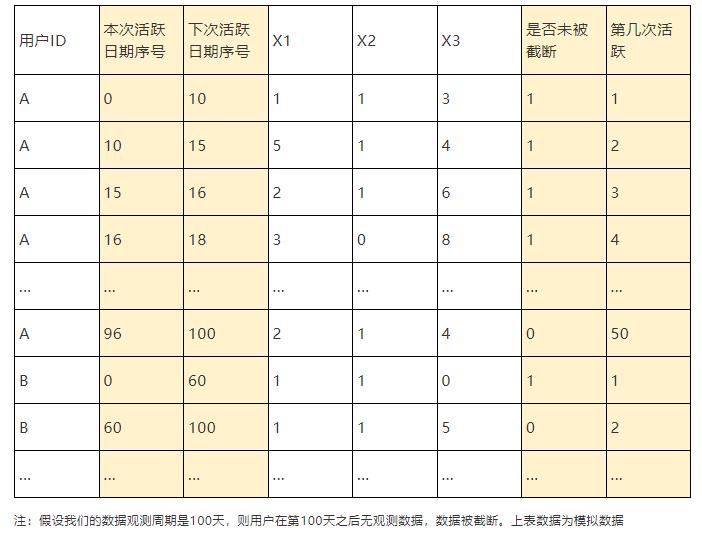
将我们关注的指标进行离散化得到dummy variables作为上表中的X1,X2,X3等一系列自变量，代入模型进行建模后得到如下结果：

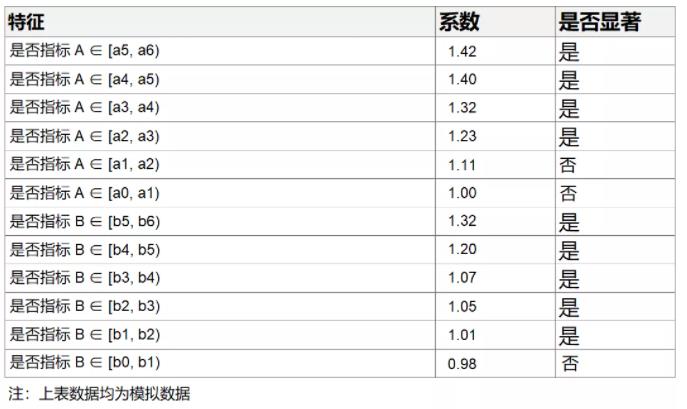
上表中显著的特征对于用户后续活跃度的提升都有显著的正向作用，而不显著的特征则对用户后续活跃度的提升无明显作用。以【是否指标A∈[a5, a6)】这一特征为例，其系数为1.42且统计学显著，则可以理解为：若某用户指标A∈[a5, a6)，则相较于baseline用户（在这里即为指标A<a0且指标B<b0）其活跃度可以提升42%。
我们可以根据各指标在何阈值以上能带来用户活跃度的显著提升来确定“优质”DAU的指标对于阈值，例如这里当指标B的阈值可以选择为b1，而指标A的阈值可以选择为a2。
我们也可以进一步的将指标做多级离散，观察随着阈值提升其对应系数的变化情况，通过系数变化的拐点来敲定指标A的阈值。具体实现方式参考下图，根据下图我们可以选取指标A的阈值为拐点对应的取值，即为a4。

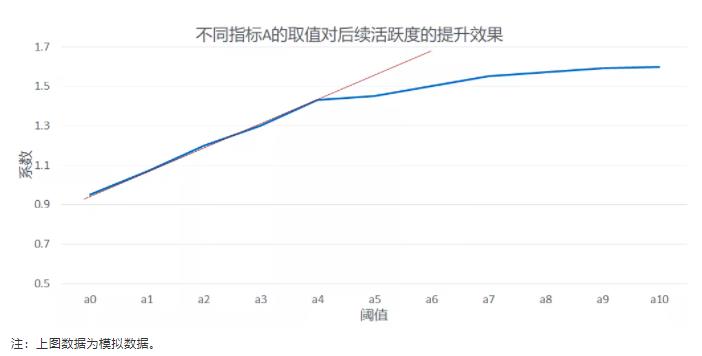
至此，我们可以利用PWP-GT模型顺利找到过去活跃度、使用时长、消费次数等指标的阈值，认为指标大于阈值的用户为高粘性用户。区别于传统的凭借业务经验定义高粘性用户的方式，我们用量化的方式实现了高粘性用户的甄别。

1.4 cox模型和 N类留存分类器

虽然使用分类器对留存概率进行建模并运用于实践是一种很流行的方式，但是当目的不仅仅是预测留存概率，且需要对背后的影响因子进行深入分析的时候，采用更合适的统计模型就非常必要了。上述模拟案例表明，当真实的数据生成过程是一个复杂的随机过程的时候，如果简单的采用二分类分类器建模，对影响因子的判断会出现较大的偏差。总结起来，主要有以下两点：

1）重复事件建模对协变量影响的估计比N日留存分类器更加贴近协变量的真实影响。
2）N日留存分类器对协变量影响的估计会随N的取值不同有较大变化，不利于确定最终结论。

1.5 延申：多结局生存分析模型

1.5.1 多结局生存分析模型分类

这是一篇论文：多结局生存分析模型与Cox模型的随机模拟比较 + 一篇文章：处理复发事件数据的几种统计模型

腾讯看点这次提及的是多结局生存分析模型，多结局现象(Multiple Failure Time Data)在各个领域都非常常见。所谓的多结局现象就是指研究对象可能出现的失效事件有多种,而不单单是经典生存分析中只有一种失效事件(即研究者所关心的结局不止一个)。
由于Cox比例风险模型为半参数模型,适用范围比较广,所以大多数多结局生存分析模型都是多结局的Cox比例风险模型,并且众多的多结局比例风险模型都是基于以下两个最基本的模型:
　　　　基本模型1: $h k (t; X k) = h 0 (t) e x p (β 1 x 1 k + β 2 x 2 k \dots + β p x p k)$ (1)
　　　　基本模型2: $h k (t; X k) = h 0 k (t) e x p (β 1 x 1 k + β 2 x 2 k \dots + β p x p k)$ (2)

各个不同的生存时间变量定义方式:

时间：

total time ：各种结局之间为无序的情况,一般采用这种时间变量定义方式,称为无序生存分析模型
counting process time / gap time：当各种结局之间为有序的情况时,可采用“counting process time”和“gap time”定义生存时间变量,故称为有序生存分析模型。

现有比较成熟的模型有PWP模型(根据模型采用的风险区间的不同可以细分为PWP-CP模型和PWP-GT模型)、AG模型、GTUR模型、WLW模型和LWA模型

该图对比腾讯看点的那张：

重复事件之间是否存在依赖 -> 有序
重复事件是否同质 -> 基础风险函数不同

按照基础风险函数和风险区间两个因素可以将六种多结局生存分析模型分类。

有序的多结局模型：PWP-CP模型、PWP-GT模型、AG模型和GTUR模型
无序的多结局模型：WLW模型和LWA模型

有序和无序多结局模型是针对同一对象发生的多种不同结局而言。

有序就是指同一对象出现的不同结局之间存在一定的顺序,例如膀胱癌的第二次复发一定是在患者第一次复发以后出现。
而在无序的情况下从研究开始时所有的对象在观察时间内发生中结局中的任意一种,例如糖尿病患者可能出现的不同的并发症(视网膜病变、神经病变等等)。

故有序和无序的生存分析模型是对应两种完全不同的情况,不可以相互混用。
基础风险函数的相同与否则必须根据实际的研究背景决定,不同的结局基础风险函数肯定不同,但相同结局的基础风险函数也可能不同,例如以孕妇出现流产为结局的研究中对象多次流产后导致的习惯性流产,此时发生相同结局(流产)的风险逐渐增大。

1.5.2 PWP模型（Prentice, Williams and Peterson，PWP)

PWP的主要思想是根据随访期间先前发生的事件数将可复发事件分层（strata）。【时变】
认为所有个体都处于第一个strata发生的风险中，但只有在先前strata中有事件的那些个体才有下一个strata的风险（先有1才有2，只有发生过一次事件的人才有发生后续事件的风险）。

它可以评估自研究开始（time=0）以来某危险因素对第k个事件的效应；也可以同时比较同一影响因素对不同结局事件的效应, 例如可以评估自研究开始（time=0）以来某危险因素对第k-1个事件的效应和对第k事件的效应；也可以评估自k-1个事件以来它对第k个事件的效应。

如果假定事件的发生会改变后续复发的风险，或者危险因素对各个事件的效应不同时，PWP更为合适。例如，事件为重复发生的病毒感染，由于首次感染后免疫力的建立，后续感染的发生会受到前次感染的影响。

需要注意的是，在实践中，事件重复次数很多的个体通常会比较少，排序靠后的strata中的个体数量少，会使估计值不可靠。因此通常需要事先将复发事件数限制为特定数量，超过这个次数的不纳入分析。例如把分析限制在复发4次以内，超过第4次的事件不分析。

1.5.3 多状态模型（Multi-state models, MSM）

MSM把事件发生看作是状态的一种“转移”，例如健康➜患病。这个模型用转移强度和转移概率两个指标来描述这种状态变化，且假设这两个参数都取决于之前所有发生的历史事件情况。MSM适合处理个体在一个有限数量（通常是少量的）的特定健康状况（包括死亡）所定义的状态间转移的情况（如下图）。复发事件可看做是个体在“健康”和“患病”两种状态间的转移，从而可以应用MSM方法。MSM的一个优势是，除了可以获得通常关注的危险因素和某个事件发生（如“健康➜患病”）的关系，还可以同时计算危险因素对多个不同事件（如“健康➜患病”，“患病➜康复”这两种状态转移）的不同影响。

1.5.4 [最常见] AG模型（Andersen-Gill，AG)

AG模型可以简单理解为Cox模型在复发事件数据中的推广。它同样假设不同事件的基础风险函数相同，且同一危险因素对不同事件的影响也相同。
该模型由两部分组成：

强度函数（intensity function）：协变量如何影响具体时间点的事件风险；
时间依存（time-dependence）：如果先前发生的事件对后续事件的发生有关联，那么这种关联被认为是由时间依存变量体现的；如果协变量不是时间依存的，则事件的复发风险不受过去事件的影响。

因此，如果事件之间的关联可以认为是由于已测量的协变量引入的，即在调整了这些协变量之后事件的发生是独立的，就可以用AG模型来解决。
换句话说，如果可以合理假设事件复发的风险和过去有无发生、或发生了多少次事件无关，可以使用AG。一般来说，如果研究只是希望得到危险因素对结局的总体影响（the overall effect on the intensity of the occurrence of a recurrent event），AG十分合适。

2 用户活跃度：快手的生存分析 for 重复事件

这里的重复事件表现为 => 活跃度

2.1 快手生存分析内容快速回顾

之前提到写过快手的用户活跃度的衡量，具体参考：生存分析——快手的基于深度学习框架的集成⽣存分析软件KwaiSurvival（一）

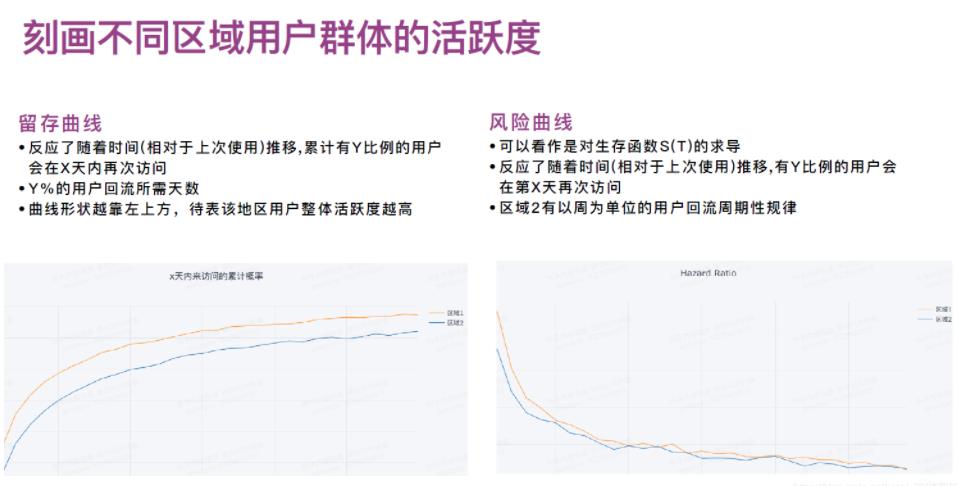
这里与腾讯看点基本类似，留存 = 活跃

2.2 指标阈值确定下腾讯看点与快手的差别

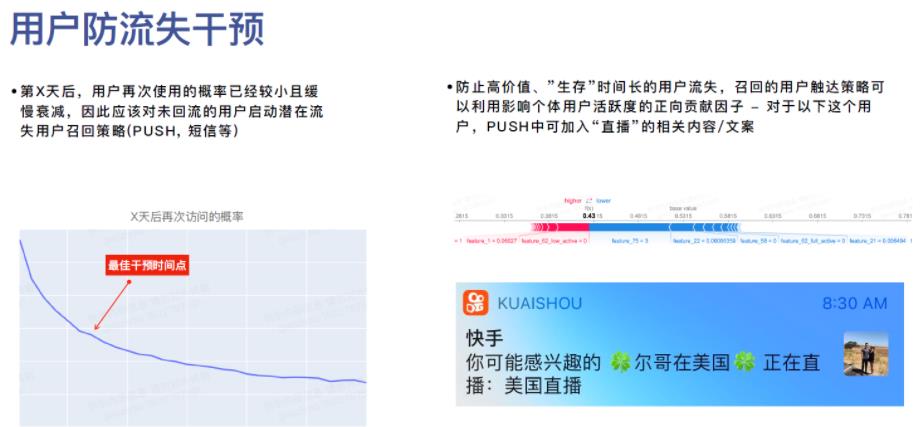
腾讯看点通过离散回归模型来选择哪些指标比较关键，快手这边是SHAP值；

腾讯看点这里，利用该模型还进行筛选指标阈值，某一个指标关键区间段（连续变量），比如影响客户活跃的某指标分类为：
过去使用时长：1-2h，2-5h，5-12h，观察随着阈值提升其对应系数的变化情况，通过系数变化的拐点来敲定指标的阈值

SHAP值也是可以的，不过好像快手里面没有提到，参考[机器学习模型可解释性进行到底 —— SHAP值理论（一）]这里可以用特征密度散点图：beeswarm：

假设LSTAT这个指标，越大（红）可能导致SHAP约低，则选择蓝/红渐变那个阶段，作为阈值

3 淘系：用户复购策略的原理与实现 Buy It Again

来自阿里巴巴淘系用户增长团队的用户复购策略的原理与实现 Buy It Again提到亚马逊的一篇：Buy It Again: Modeling Repeat Purchase Recommendations

此时，重复事件 —> 复购

亚马逊总部Seattle研究院的工作，问题非常简单，就是研究网络用户的重复购买行为，传统研究一般是根据用户兴趣研究用户未来可能购买什么东西（大家骨子里的思维方式都是用户不会再购买已经买过的商品，比如电视机），然而事实上很多购买行为都是重复购买，比如买牙膏、或者买某些消费品，用户反而倾向于买已经买过的商品，作者把这个问题叫做Repeat Purchase。
这篇文章提出一个Poisson-Gamma模型（PG）以及他的扩展版本（MPG），后来在离线数据上得到了一定的提升。

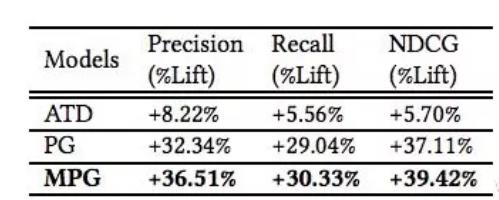
3.1 复购机会与复购几率

问题描述：基于用户历史购买某个商品的行为数据，构建一个复购概率的预测函数，预测用户在某个时刻进行复购的概率。

这里拆分成了复购可能性和复购时机：
复购可能性：RCP（repeat customer probability）的指标，对于商品；作为复购商品的筛选指标：满足 RCP > 阈值 的商品，我们可以认为是复购商品。

复购时机:
一些商品，有许多人会进行复购，可以利用人群的购买间隔推断出商品复购时间的分布规律。

计算过程如下：

对于每个商品，计算复购用户的平均购买间隔：首次购买距今天数/购买次数（分布示例如下所示）
用常见的概率分布（Log-Normal、Gamma分布等）去拟合购买间隔的分布

计算示例（此时可乐曝光优先级将高于纸巾）：
针对这种方式，我们也做过线上实验，从效果来看：曝光点击转化率降低，点击购买转化率提升。可以推测，因为只推荐复购商品，用户选择范围变小、导致点击率降低，但点进去的用户是有复购需求的用户、从而购买率上升。

3.2 PG-model 应用方式

用户（人群）筛选：设定阈值 $x$ ，当用户有1个或以上类目复购概率大于 $x$ 时进入复购策略干预人群。可以理解为这些人是有复购需求的，我们才可以用复购策略进行干预；
底池圈选（召回）：针对每个用户，将复购概率大于 $x$ 的商品作为货品底池；
将复购概率表作为特征提供给算法同学，协助进行精排。

其他需要注意的地方

通常会基于类目而不是货品进行预测，（如纸巾是类目，维达卷纸是货品），避免数据太过稀疏；
购买间隔的计算口径（前者更准、后者计算更简单）：
- a. 一段时间内首次购买与末次购买之间时长/（购买天数-1）
- b. 180天/180天内购买天数；
计算时需要排除退货的购买，需考虑大促带来的影响（根据规则剔除大促带来的短周期复购）。

3.3 延申：BG/NBD概率模型预测用户生命周期LTV

之前笔者写过的用户增长 - BG/NBD概率模型预测用户生命周期LTV（二）里面把每个用户的复购问题拆分为：交易次数+流失率
该模型可利用用户历史交易数据(RFM)来预测未来每个用户的交易次数和流失率。

3.3.1模型假设前提

该模型的几个假设前提：

（1）【交易假设】用户在活跃状态下，一个用户在时间段t内完成的交易数量服从均值为λt的泊松分布。

【交易假设】用户的交易率λ服从形状参数为r，逆尺度参数为α的gamma分布，PDF函数如下所示。

每个客户有自己的Buy Coin，每个Coin的正反面出现的概率是不一样的。上图模拟了以形状参数为9，尺度参数为0.5的Gamma分布建模的100个客户的泊松分布

【流失假设】每个用户在交易j完成后流失的概率服从参数为p(流失率)的几何分布，PDF函数如下所示

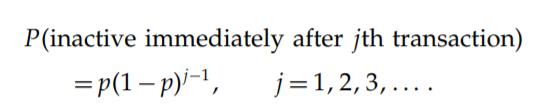
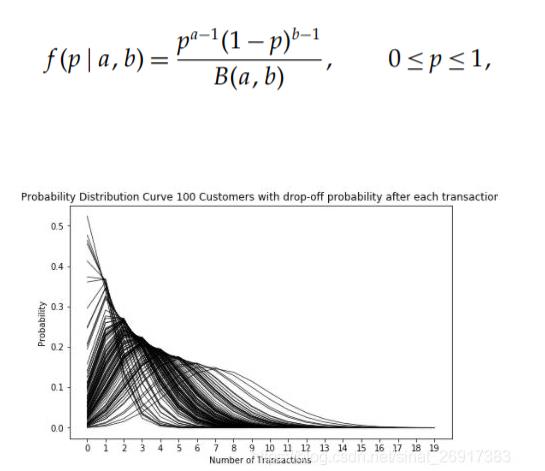
【流失假设】用户的流失率p服从形状参数为a，b的beta分布，PDF函数如下所示。比如100个用户的流失率p服从a=1.0，b=2.5的beta分布时，这100个用户的几何分布图如下所示：

3.3.2 客群分析的应用

在[2.2 BG-NBD模型用于客群分析]提到，
流失率p- beta分布求解
模型原理：首先gamma分布和beta分布分别为参数交易率λ和流失率p的先验分布，而泊松分布和几何分布是样本的分布函数，即似然函数。接下来建立交易率λ和流失率p的联立似然函数，使用Nelder-Mead的单纯形算法求解gamma分布和beta分布中的参数(r，α，a，b)，这是一种启发式的，非梯度搜索方法来最小化负对数似然代价函数。

为预测每个用户在未来一段时间内的交易次数，这里推导出条件期望，

根据用户历史的交易次数和交易时间数据，并根据上面得到的分布函数参数值，条件期望的最终计算公式如下所示：

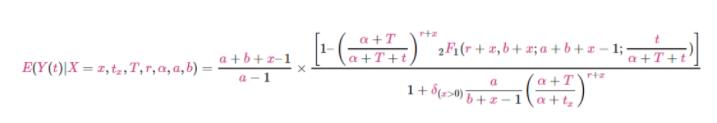
def calculate_conditional_expectation(t, x, t_x, T):
    first_term = (a + b + x - 1) / (a-1)
    hyp2f1_a = r + x
    hyp2f1_b = b + x
    hyp2f1_c = a + b + x - 1
    hyp2f1_z = t / (alpha + T + t)
    hyp_term = hyp2f1(hyp2f1_a, hyp2f1_b, hyp2f1_c, hyp2f1_z)
    second_term = (1 - ((alpha + T) / (alpha + T + t)) ** (r + x) * hyp_term)
    delta = 1 if x > 0 else 0
    denominator = 1 + delta * (a / (b + x - 1)) * ((alpha + T) / (alpha + t_x)) ** (r+x)
    return first_term * second_term / denominator


calculate_conditional_expectation(39, 2, 30.43, 38.86)
>>> 1.225904664486748

某用户过去38.86周内(T=38.86)交易两次(x=2) 第二次交易时间为30.43周(tx=30.43)的条件计算得到该用户在未来39周将交易1.226次。

通过预测出每个用户未来的交易次数，可以更针对性地细分用户人群，找准目标价值人群从而制定细分运营方案，比如未来一年52周用户预测出将交易1次，那么该用户有流失的风险，那么在现阶段实施促销方案（如发放促销卡），提高用户的交易频次将减小用户流失的风险。

3.4 数据分布的拟合：fitter

淘系那篇有提到fitter的使用：通过python拟合数据分布的利器 - fitter
从样本数据中识别（拟合）出生成该样本数据的底层（连续）概率分布，或者说这些数据服从的分布。

# 数据生成
from scipy import stats
data = stats.gamma.rvs(2, loc=1.5, scale=2, size=10000) # 通过scipy生成服从gamma分布的10000个样本
# 拟合分布
from fitter import Fitter
f = Fitter(data)  # 创建Fitter类
f.fit()  # 调用fit函数拟合分布
f.summary()  # 输出拟合结果

以上的代码输出了对数据拟合效果最好的五个分布以及对应的误差，同时绘制了数据的分布&分布的拟合情况:

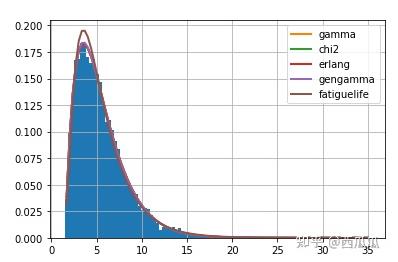
主函数的说明：

classfitter.fitter.Fitter(data, xmin=None, xmax=None, bins=100, distributions=None, timeout=30, density=True)

distributions：待拟合的分布，若不指定则会遍历上面提到的80个分布（会耗时较长）。eg. distributions = [‘gamma’, ‘erlang’]；
xmin, xmax：截断样本数据的范围，小于xmin或大于xmax的数据会被忽略；
timeout：单个分布拟合的最大时长，超过该值改分布会被遗弃，默认值为30，单位为秒。一般使用时我会将其调大为100秒，避免一些合适的分布被略去。
density通常设为True，bins为绘制直方图（histogram）时的分段数、默认不改，当有outlier时可适当扩大。

拟合模块：

f = Fitter(data, distributions=['gamma', 'rayleigh', 'uniform'], timeout =10000)
f.fit()

f.fitted_param[‘gamma’]: 某个分布的最佳参数
f.fitted_pdf[‘gamma’]: 用最佳参数生成的PDF
f.get_best() 返回最佳的拟合分布以及参数（dictionary的格式）
f.hist() 绘制样本数据的normed histogram（面积为1的直方图）
f.plot_pdf(names=None, Nbest=5, lw=2, method=‘sumsquare_error’) 绘制拟合分布的PDF（概率密度函数），names：需要绘制的分布名，lw: 线宽.
summary(Nbest=5, lw=2, plot=True, method=‘sumsquare_error’): 返回最好的Nbest个分布及误差，绘制分布图
f.distributions 用于拟合的分布

然后可以简单来看看：

from scipy import stats
data = stats.gamma.rvs(2, loc=1.5, scale=2, size=10000) # 通过scipy生成服从gamma分布的10000个样本
# 拟合分布
from fitter import Fitter
f = Fitter(data)  # 创建Fitter类
f.fit()  # 调用fit函数拟合分布

a = f.x
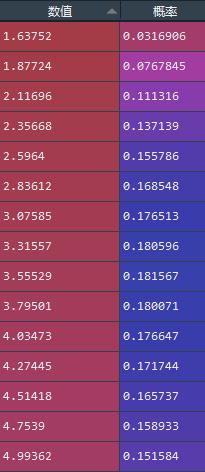
b = f.fitted_pdf['gamma']
c = pd.DataFrame(zip(a,b),columns = ['数值','概率'])

这里可以简单来看看，如何拿到gamma分布的概率密度值：