数学建模天天学_第三天_非线性规划

Posted 2021-12-10 再吃一个橘子

川川菜鸟关于非线性贵第一小节的学习内容pdf

 

 

自我理解：

1.为什么要有非线性规划？

对于生活中的大多数数据，并不一定是线性的，不可避免会存在非线性的数据。

如果目标函数或者约束条件中包含非线性函数，就称这种规划问题为非线性规划问题。

2.非线性规划函数 - fmincon

fmincon函数是用于寻找约束非线性多变量函数的最小值，其用法是：

语法格式

x = fmincon(fun,x0,A,b) 从 x0 开始，尝试在满足线性不等式 A*x ≤ b 的情况下寻找 fun 中所述的函数的最小值点 x。x0 可以是标量、向量或矩阵。
x = fmincon(fun,x0,A,b,Aeq,beq) 在满足线性等式 Aeq*x = beq 以及不等式 A*x ≤ b 的情况下最小化 fun。如果不存在不等式，则设置 A = [] 和 b = []。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) 对 x 中的设计变量定义一组下界和上界，使解始终在 lb ≤ x ≤ ub 范围内。如果不存在等式，请设置 Aeq = [] 和 beq = []。如果 x(i) 无下界，请设置 lb(i) = -Inf，如果 x(i) 无上界，请设置 ub(i) = Inf。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) 使用 options 所指定的优化选项执行最小化。使用 optimoptions 可设置这些选项。如果没有非线性不等式或等式约束，请设置 nonlcon = []。

参数解释：

b 和 beq 是向量，A 和 Aeq 是矩阵，c(x) 和 ceq(x) 是返回向量的函数，f(x) 是返回标量的函数。f(x)、c(x) 和 ceq(x) 可以是非线性函数。
x、lb 和 ub 可以作为向量或矩阵传递

3.线性不等式约束

目标函数：

fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;%匿名函数

约束条件：

从点[-1，2]为起点求最小值，约束方程x(1)+2x(2)<=1

matlab代码：

fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;%匿名函数
x0 = [-1,2];%起点可以更改，似乎没影响
A = [1,2];
b = 1;
[x,y] = fmincon(fun,x0,A,b)%套用函数

执行结果：

 

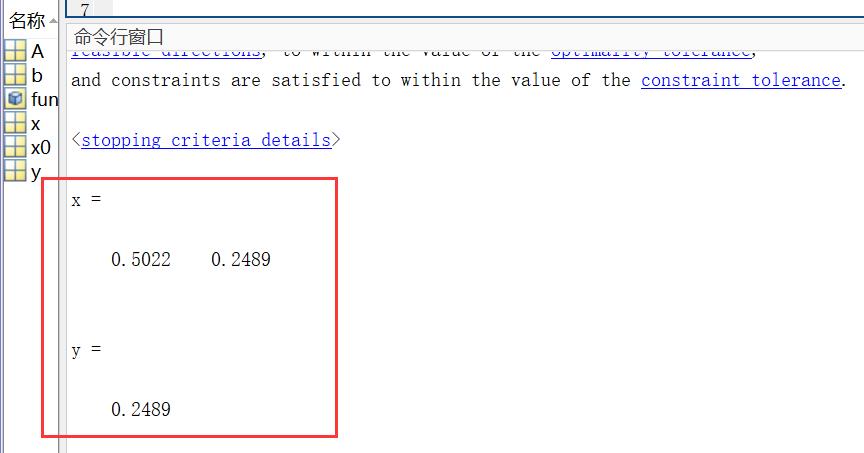
4.线性不等式和等式约束

求解这个：

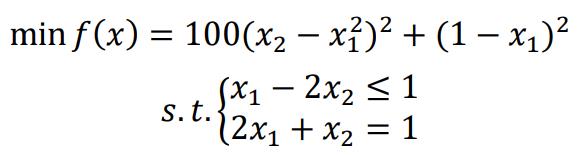
 matlab代码：

clc
clear all
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;

x0 = [1,1];%初始点设置自行不同
A = [1,-2];
b = 1;
Aeq = [2,1];
beq = 1;
[x,y] = fmincon(fun,x0,A,b,Aeq,beq)

执行结果：

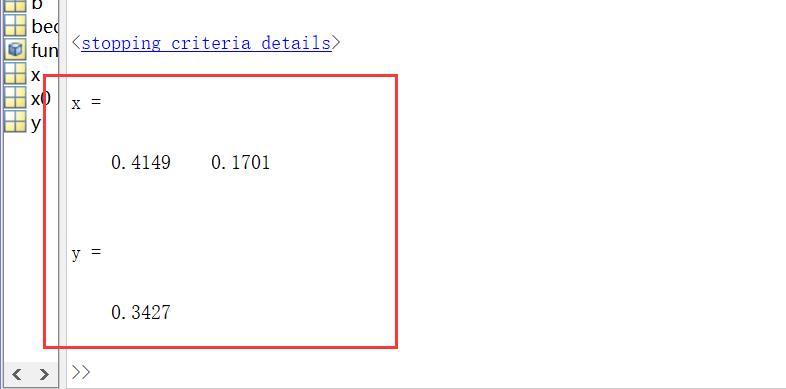
5.求带非线性约束的最值

目标函数：

min f (x) = x1^2 + x2^2 + x3^2 + 8

约束条件：

x1^2 − x2 + x3 ^2 ≥ 0
x1 + x2^2 + x3 ^3 ≤ 20
− x1 − x2^2 + 2 = 0
x2 + 2x3^2 = 3x1
x1,x2 , x3 ≥ 0

matlab代码：

clc
clear all
% 主函数
options=optimset('largescale','off');
%[x,y] = fmincon(fun,rand(3,1),[],[],[],[],zeros(3,1),[], @nonlcon, options)

[x,y] = fmincon('fun',rand(3,1),[],[],[],[],zeros(3,1),[],'nonlcon')
 
% 目标函数
function f=fun(x)
f=sum(x.^2)+8;
end
 
% 非线性约束条件
function [c,ceq]=nonlcon(x)
c=[-x(1)^2+x(2)-x(3)^2
    x(1)+x(2)^2+x(3)^3-20];  %非线性不等式约束
ceq=[-x(1)-x(2)^2+2
   x(2)+2*x(3)^2-3]; %非线性等式约束
end

匿名函数：