matlab改进（结合聚类）头脑风暴算法求解路径优化问题VRP

Posted 2021-12-10 张叔zhangshu

tic
clear
clc
%% 用xlsread函数来读取xlsx文件
data=xlsread('实例验证数据.xlsx','转换后数据','A2:H17');
cap=150;                            %车辆最大装载量
v=30/60;                            %车辆行驶速度=30km/h=30/60km/min
%% 提取数据信息
E=data(1,6);                        %配送中心时间窗开始时间
L=data(1,7);                        %配送中心时间窗结束时间
vertexs=data(:,2:3);                %所有点的坐标x和y
customer=vertexs(2:end,:);          %顾客坐标
cusnum=size(customer,1);            %顾客数
v_num=10;                           %车辆最大允许使用数目
demands=data(2:end,4);              %需求量
pdemands=data(2:end,5);             %回收量
a=data(2:end,6);                    %顾客时间窗开始时间[a[i],b[i]]
b=data(2:end,7);                    %顾客时间窗结束时间[a[i],b[i]]
s=data(2:end,8);                    %客户点的服务时间
h=pdist(vertexs);
dist=squareform(h);                 %距离矩阵
N=cusnum+v_num-1;                   %解长度=顾客数目+车辆最多使用数目-1
%% 参数初始化
alpha=10;                           %违反的容量约束的惩罚函数系数
belta=100;                          %违反时间窗约束的惩罚函数系数
MAXGEN=150;                         %最大迭代次数
NIND=50;                            %种群数目
cluster_num=5;                      %聚类数目
p_replace=0.1;                      %用随机解替换一个聚类中心的概率
p_one=0.5;                          %选择1个聚类的概率
p_two=1-p_one;                      %选择2个聚类的概率，p_two=1-p_one
p_one_center=0.3;                   %选择1个聚类中聚类中心的概率
p_two_center=0.2;                   %选择2个聚类中聚类中心的概率
%% 种群初始化
Population=InitPop(NIND,N);
%% 主循环
gen=1;                              %计数器初始化
bestInd=Population(1,:);            %初始化全局最优个体
bestObj=ObjFunction(bestInd,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);  %初始全局最优个体的目标函数值
BestPop=zeros(MAXGEN,N);            %记录每次迭代过程中全局最优个体
BestObj=zeros(MAXGEN,1);            %记录每次迭代过程中全局最优个体的目标函数值 
BestTD=zeros(MAXGEN,1);            %记录每次迭代过程中全局最优个体的总距离
while gen<=MAXGEN
    %% 计算目标函数值
    Obj=ObjFunction(Population,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
    %% K-means聚类
    Idx=kmeans(Obj,cluster_num,'Distance','cityblock','Replicates',2);
    cluster=cell(cluster_num,2);                    %将解储存在每一个聚类中
    order_cluster=cell(cluster_num,2);              %将储存在每一个聚类中的个体按照目标函数值排序
    for i=1:cluster_num
        cluster{i,1}=Population(Idx==i,:);          %将个体按照所处的聚类编号储存到对应的聚类中
        cluster_row(i)=size(cluster{i,1},1);           %计算当前聚类中个体数目
        for j=1:cluster_row(i)
            Individual=cluster{i,1}(j,:);           %当前聚类中第j个个体
            %计算当前聚类中第j个个体的目标函数值
            cluster{i,2}(j,1)=ObjFunction(Individual,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
        end
        [order_cluster{i,2},order_index]=sort(cluster{i,2}) ; %将当前聚类中的所有个体按照目标函数值从小到大的顺序进行排序
        order_cluster{i,1}=cluster{i,1}(order_index,:); %将当前聚类中的所有个体按照排序结果重新排列
        order_index=0;                                  %重置排序序号
    end
    cluster_fit=cell2mat(order_cluster);                %将聚类的元胞数组转换为矩阵，最后一列为个体的目标函数值
    %% 以一定的概率随机从m个聚类中心中选择出一个聚类中心，并用一个新产生的随机解更新这个被选中的聚类中心
    order_cluster=replace_center(p_replace,cluster_num,N,order_cluster,...
    v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
    %% 更新这n个个体
    Population=update_Population(Population,cluster_num,cluster_row,Idx,order_cluster,p_one,p_one_center,p_two_center...
    ,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
    %% 计算原始Population的目标函数值
    Obj=ObjFunction(Population,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
    %% 从更新后的Population中选择目标函数值在前50%的个体
    offspring=select(Population,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
    %% 对选择出的个体进行局部搜索操作
    offspring=LocalSearch(offspring,v_num,cusnum,a,b,s,L,dist,demands,pdemands,cap,alpha,belta,v);
    %% 将局部搜索后的offspring与原来的Population进行合并
    Population=merge(Population,offspring,Obj);
    %% 计算合并后的Population的目标函数值
    mObj=ObjFunction(Population,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v,alpha,belta);
    %% 找出合并后的Population中的最优个体
    [min_len,min_index]=min(mObj);               %当前种群中最优个体以及所对应的序号
    %如果当前迭代最优个体目标函数值小于全局最优目标函数值，则更新全局最优个体
    if min_len<bestObj
        bestObj=min_len;
        bestInd=Population(min_index,:);
    end
    %% 打印各代最优解
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestInd,v_num,cusnum,cap,demands,pdemands,a,b,s,L,dist,v);
     disp(['目标函数值：',num2str(bestObj),'，车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD),'，违反约束路径数目：',num2str(best_vionum),'，违反约束顾客数目：',num2str(best_viocus)]);
    fprintf('\\n')
    %% 距离全局最优个体
    BestObj(gen,1)=bestObj;                     %记录全局最优个体的目标函数值 
    BestPop(gen,:)=bestInd;                     %记录全局最优个体
    BestTD(gen,1)=bestTD;                       %记录全局最优个体的总距离 
    %% 计数器加1
    gen=gen+1;
end
%% 画出最优配送路线图
draw_Best(bestVC,vertexs);
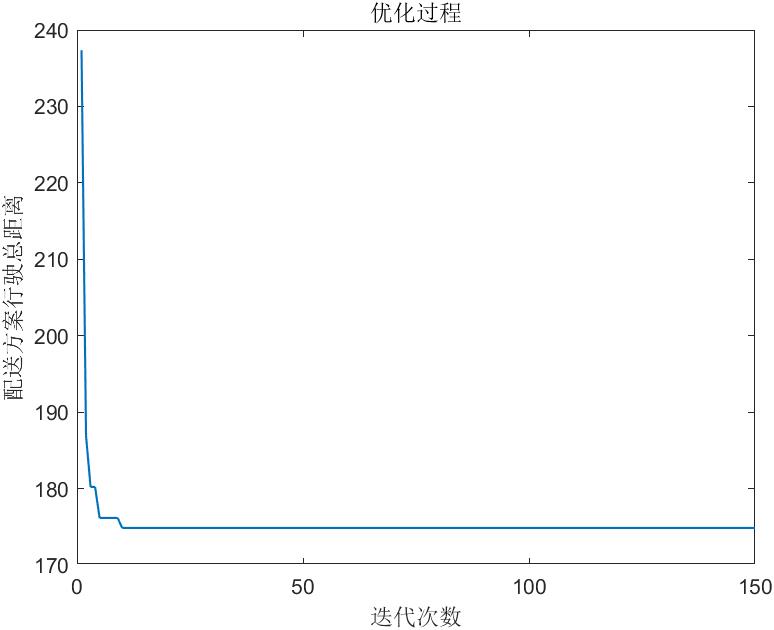
%% 打印每次迭代的全局最优个体的总距离变化趋势图
figure;
plot(BestTD,'LineWidth',1);
title('优化过程')
xlabel('迭代次数');
ylabel('配送方案行驶总距离');
toc