TSP基于matlab自重启伪遗传改良算法求解旅行商问题含Matlab源码 1510期

Posted 2021-12-10 紫极神光

一、获取代码方式

获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

获取代码方式2：
通过紫极神光博客主页开通CSDN年度会员，凭支付凭证，私信博主，可获得此代码。

获取代码方式3：
完整代码已上传我的资源：【TSP】基于matlab自重启伪遗传改良算法求解旅行商问题【含Matlab源码 1510期】

备注：开通CSDN年度会员，可免费获得1份代码（有效期为开通日起，三天内有效）；
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、TSP简介

旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP的数学模型

三、遗传算法简介

1 引言


2 遗传算法理论
2.1 遗传算法的生物学基础


2.2 遗传算法的理论基础




2.3 遗传算法的基本概念






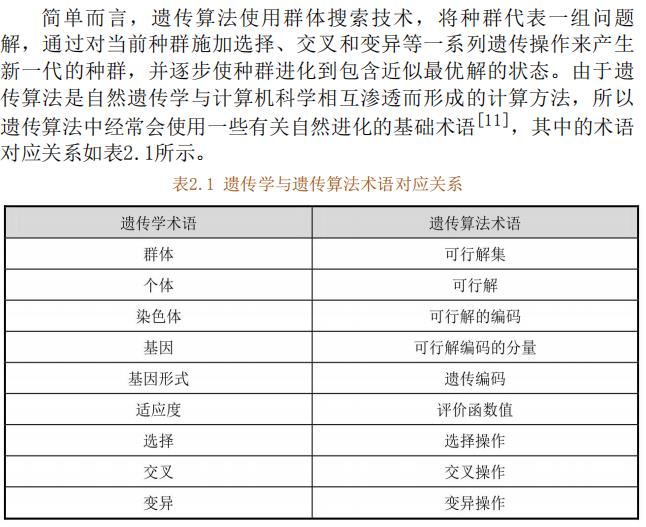
2.4 标准的遗传算法


2.5 遗传算法的特点


2.6 遗传算法的改进方向

3 遗传算法流程



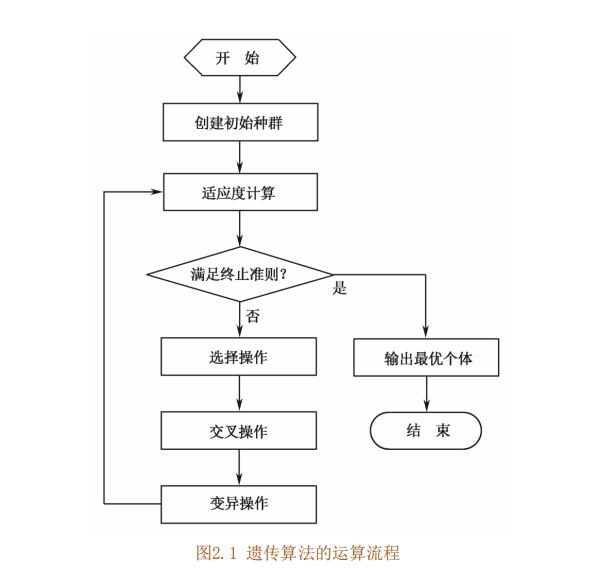
4 关键参数说明

四、部分源代码

tic
clc,clear
rng('shuffle');         %改变随机数的初始状态

% -----------------参数------------------
w = 500;                        % 种群规模
restart_times = 200;             % 重启次数
iterations = 300;               % 迭代次数
repeat_time_threshold = 100;    % 重复次数阈值
% ---------------------------------------

% 从文件中读取信息
load ch130.mat          % 载入数据集
point_info = ch130(:, 2:3);            
point_position_x_and_y = [point_info; point_info(1,:)];  
distance_matrix = get_distance_matrix(point_info);

L = length(ch130) + 1;              % 为了保证最终能回到起点，实际的个体长度设为L，L的最后一个数和第一个数相同，保证回到起点

optimal_path = zeros([1, L]);       % 记录全局最佳路径
optimal_path_length = 999999;       % 记录全局最佳路径的长度

for r_index = 1:restart_times
    
    current_optimal_path = zeros([1, L]);                       % 记录每次重启的最佳路径
    current_optimal_path_length = 999999;                       % 记录每次重启的最佳路径长度
    last_optimal_path_length = current_optimal_path_length;     % 记录单次遗传算法中上一次最佳路径长度，用于判断是否陷入局部最优解
    same_time = 0;                                              % 单次遗传算法陷入局部最优解的次数

    % 产生初始种群
    initial_population = generate_population(w, L);

    % 改良圈改良初始种群
    A = circle_modification(initial_population, w, L, distance_matrix);

    % 归一化
    A = normalization(A, L);

    % 以下为遗传算法实现过程
    for k=1:iterations

        % 交叉产生子代 B
        B = cross(A, w, L, distance_matrix);

        % 变异产生子代 C
        C = mutation(A, w, L, distance_matrix);

        % 选择下一代
        [A, current_optimal_path, current_optimal_path_length] = select_next_generation(A, B, C, w, L, distance_matrix);
        
        % 更新全局最优路径长度
        if current_optimal_path_length < optimal_path_length
            optimal_path_length = current_optimal_path_length;
            optimal_path = current_optimal_path;
        end

        % 绘制最优路径图
        plot_path(point_position_x_and_y, current_optimal_path, current_optimal_path_length)     

        % 输出每次迭代的信息
        fprintf('第%0d次重启，迭代次数%04d，最优路径长度%.5f，全局最优路径长度%.5f\\n' , r_index, k, current_optimal_path_length, optimal_path_length); 
        
        % 记录重复次数（重复次数过高表示陷入局部最优解）
   
           end
        else   
            same_time = 0;  % 重置same_time
        end
        
        % 更新last_optimal_path_length
        last_optimal_path_length = current_optimal_path_length;
        
    end

end 

toc                                                                      % 输出程序运行的时间
function [ distance_matrix ] = get_distance_matrix( point_info )
% 获取距离矩阵
number_of_point = length(point_info);
D = pdist(point_info,'euclidean');  % 每两点之间的欧式距离，矩阵大小为(1,n)
distance_matrix = zeros(number_of_point + 1);      % 每次都要回到起点，因此，最后一列为到起点的距离
sum = 0;
for i = 1:number_of_point             
     if i < number_of_point
         sum = sum + number_of_point - i;
         distance_matrix(i, i+1:number_of_point) = D(1, sum-(number_of_point-i-1):sum);   % 将已知的D距离改为矩阵形式
     end
end
distance_matrix = distance_matrix + distance_matrix';
distance_matrix(1:number_of_point, number_of_point+1) = distance_matrix(1:number_of_point, 1);         % 对最后一列进行填值
distance_matrix(number_of_point+1, :) = distance_matrix(1, :);                               % 对最后一行进行填值，完整的距离矩阵

end

function [ A_next, optimal_path, optimal_path_length ] = select_next_generation( A, B, C, w, L, distance_matrix )
% 选择遗传的下一代

fp = 0.3;                               % 外来人口比例
np = 0.2;                               % 非最优比例

G = [A;B;C];                            % A为原始的，B为交叉后的，C为变异后的
total_length = size(G, 1);              % 父代和子代的总长度

%在父代和子代中选择优良品种作为新的父代
[~, path_table] = sort(G,2);               % 对每一行的元素进行排序，获取所有的路径
all_path_length = [];
all_path_length(1:total_length) = 0;            % 初始化所有路径的长度为0
for path_index = 1:total_length                 % 计算每条路径的长度
    for i = 1:L-1   
        all_path_length(path_index) = all_path_length(path_index) + distance_matrix(path_table(path_index, i), path_table(path_index, i+1));
    end
end

[sorted_length, sorted_index] = sort(all_path_length);      
A_next = G(sorted_index(1:w), :);                   %选出距离最短的w个子代
optimal_path = path_table(sorted_index(1), :);      % 此时的最短路径为第1个个体
optimal_path_length = sorted_length(1);             % Dz为该最短路径的实际距离

% 人人能娶老婆
up_n = w*(1-np-fp);
for i = up_n+1:w*(1-fp)
    r = up_n + unidrnd(w - up_n);
    A_next(i) = G(r);
end

% 加入外来人口，但是前提是要对外来人口进行优化，不能把一些垃圾人种加进来
A_next(int16(w*(1-fp))+1:w, :) = normalization(circle_modification(generate_population(int16(w*fp), L), int16(w*fp), L, distance_matrix), L);

五、运行结果

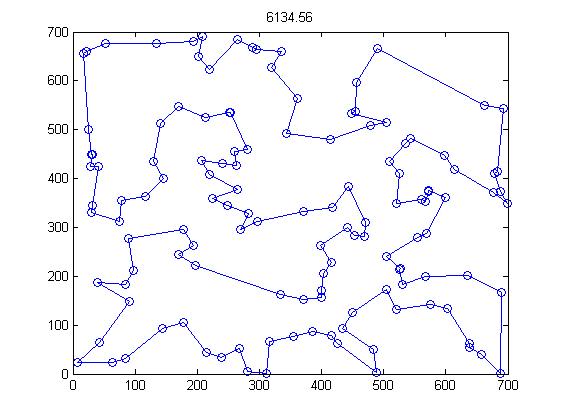
六、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.