TSP基于matlab自适应动态邻域布谷鸟混合算法求解旅行商问题含Matlab源码 1513期

Posted 2021-12-10 紫极神光

一、 TSP简介

旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP的数学模型

二、布谷鸟算法简介

布谷鸟算法，英文叫做Cuckoo search (CS algorithm)。首先还是同样，介绍一下这个算法的英文含义， Cuckoo是布谷鸟的意思，啥是布谷鸟呢，是一种叫做布谷的鸟，o(∩_∩)o ，这种鸟她妈很懒，自己生蛋自己不养，一般把它的宝宝扔到别的种类鸟的鸟巢去。但是呢，当孵化后，遇到聪明的鸟妈妈，一看就知道不是亲生的，直接就被鸟妈妈给杀了。于是这群布谷鸟宝宝为了保命，它们就模仿别的种类的鸟叫，让智商或者情商极低的鸟妈妈误认为是自己的亲宝宝，这样它就活下来了。
布谷鸟搜索算法（Cuckoo Search, CS）是2009年Xin-She Yang 与Suash Deb在《Cuckoo Search via Levy Flights》一文中提出的一种优化算法。布谷鸟算法是一种集合了布谷鸟巢寄生性和莱维飞行（Levy Flights）模式的群体智能搜索技术，通过随机游走的方式搜索得到一个最优的鸟巢来孵化自己的鸟蛋。这种方式可以达到一种高效的寻优模式。

1 布谷鸟的巢寄生性

2 莱维飞行

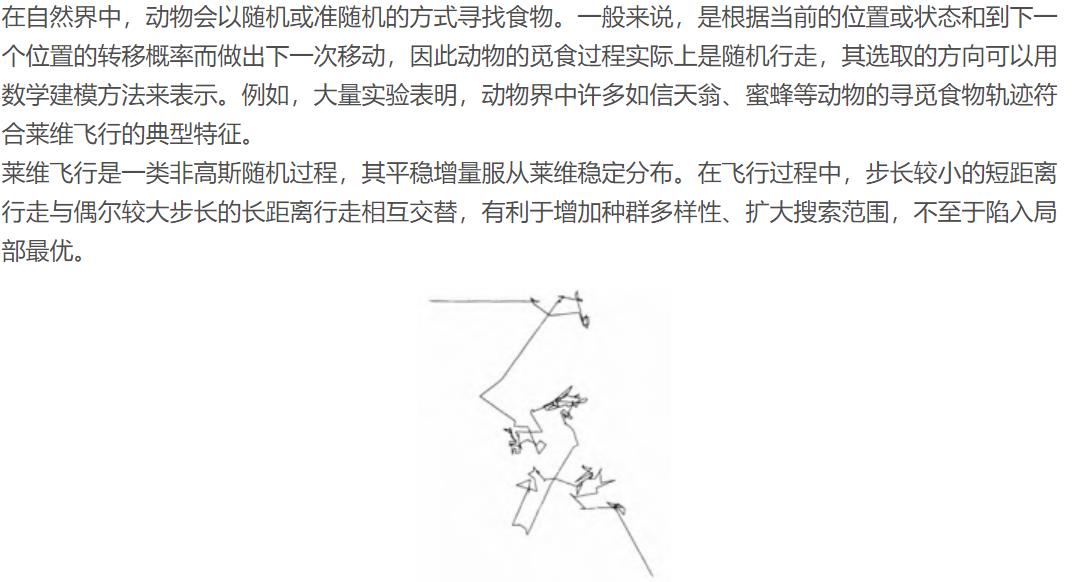
图1.模拟莱维飞行轨迹示意图

3 布谷鸟搜索算法的实现过程

三、部分源代码

clc;
A = load('berlin52.txt'); % 数据集
pop = 20;    % 种群数
gem = 500;   % 迭代次数
Pa = 0.2;    % 鸟巢发现概率 
[bestck, best_lenck]=finalver(A,pop,Pa,gem);     % 单次调用

% 循环30次取平均
a = 0;
for i=1:5
      [bestckr, best_lenckr]=finalver(A,pop,Pa,gem);
      a(i)=best_lenckr;
end
besta = min(a);
avra = mean(a,2);
besta
avra
function [best, bestsofar] = finalver(A,pop,Pa,gem)
figure('name','testTSP');
% 画出散点图
plot(A(:,2),A(:,3),'s','markersize',2);   

% 截取数据点坐标
X=A(:,2:3);  
Mdl = KDTreeSearcher(X);    % 筛选最近邻

%初始化参数定义部分
[N,~]=size(A);              % 获取城市数
D=distance(A);              % 生成距离矩阵
PP=zeros(pop,N+1);
P0=zeros(pop,N+1);
for i=1:pop
    P0(i,2:N)=randperm(N-1)+1;    % 随机生成初始群体P0
end

for i=1:pop
    PP(i,:)=[1 P0(i,2:N) 1];      % 修改形成初始群体PP,添加起点终点
end

% 构造改良圈算法初始矩阵
for k=1:pop
    flag=1;
    while flag
        flag=0;
        for i=1:N-2
            for j=i+2:N
                if D(PP(k,i),PP(k,j))+D(PP(k,i+1),PP(k,j+1))<D(PP(k,i),PP(k,i+1))+D(PP(k,j),PP(k,j+1))
                   PP(k,(i+1):j)=PP(k,j:-1:(i+1));
                   flag=1;
                 end
             end
         end
     end
end

P1 = PP(:, 1:N);               % 截取路程
fit_ret = fitness(P1, D);      % 计算适应度函数
[route_sr,best_sr] = sort(fit_ret);    % 适应度排序
best_len = route_sr(1);       % 当前最短路径总和
best = P1(best_sr(1), :);     % 截取子路程
bestsofar = best_len;
total = gem;
tabulength= 5+N; % 禁忌长度 % 
global tabulist;
% 初始化禁忌表
for i = 1:tabulength
   tabulist(i).list= 0;
   tabulist(i).value= 0;
end
% 开始迭代
while gem
    % 种群选择 parfor帮助提速
    parfor i=1:pop              
        B = P1(i,:);
        locbest = fitness(B, D);    % 计算适应度 
        bestch = B;                 % 暂存结果
        temp = rand;                
        if temp < (0.5-0.1*(1/(1+exp(-(gem-450)/10)))-0.2*(1/(1+exp(-(gem-250)/10))))                 %列维飞行，长短距离
            choice = 1;  % 2-opt邻域
        elseif temp > (0.9-0.3*(1/(1+exp(-(gem-450)/10))))     
            choice = 4;  % 双桥邻域
        else  
            choice = 2;  % 3-opt邻域
        end
        switch choice
            case 1
                [E] = crossover(Mdl,A,B,D,1,gem);           % 2-opt邻域
            case 2
                if gem > 350
                     [E] = crossover(Mdl,A,B,D,3,gem);      % 3-opt前期
                else
                     [E] = crossover(Mdl,A,B,D,2,gem);      % 3-opt后期
                end 
            case 4
                 [E] = crossover(Mdl,A,B,D,4,gem);          % 双桥邻域
        end
        C = E;
        Fitnc = fitness(C,D);      % 计算适应度 
        if Fitnc < locbest
            bestch = C;
            locbest = Fitnc;
        end 
       
        % 鸟巢被发现 
        if rand < Pa                  
               [F] =  crossover(Mdl,A,B,D,4,500);           % 双桥邻域
               G = F;
               Fitnc = fitness(G,D);                    % 计算适应度 
               if Fitnc < locbest
                  bestch = G;
               end 
        end
        P1(i,:) = bestch;
    end

    P = P1;
    fit_ret = fitness(P, D);              % 计算适应度函数
    [route_sr,best_sr] = sort(fit_ret);   % 适应度排序
    best_len = route_sr(1);               % 当前最短路径总和
    best = P(best_sr(1) ,:);              % 截取子路程
    % 更新最优解
    if bestsofar > best_len
        bestsofar = best_len;
    end
    Saver(1,total - gem+1) = bestsofar;    %存储每次的最优解
    gem = gem-1;     % 进入下一次循环
end

% 画出闭合路径曲线图
scatter(A(:,2),A(:,3),'x');
hold on;
plot([A(best(1),2),A(best(N),2)],[A(best(1),3),A(best(N),3)]);
hold on;
title(best_len)  %添加图像标题
for i=1:N-1
    x0=A(best(i),2);
    x1=A(best(i+1),2);
    y0=A(best(i),3);
    y1=A(best(i+1),3);
    xx=[x0, x1];
    yy=[y0, y1];
    plot(xx,yy);
    hold on;
end

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.