通信原理实验三 数字基带码型产生实验
Posted 毛_三月
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了通信原理实验三 数字基带码型产生实验相关的知识,希望对你有一定的参考价值。
目录
一、实验目的
1、掌握数字基带传输码型的特点;
2、掌握常用的数字基带传输码的产生方法;
3、能用matlab编写程序产生一些常用的码型,如RZ、NRZ、AMI、HDB3、双相码等。
二、实验器材
计算机,MATLAB软件
三、实验原理
1、数字基带信号
设消息代码由二进制符号0和1组成
(1)单极性码:基带信号的0电位及正电位分别与二进制符号的0与1对应;
(2)双极性码:二进制符号0、1分别与正、负电位相对应;
(3)单极性归零码:有电脉冲比码元宽度窄,每个脉冲都回到零电位;
(4)双极性归零码:相邻脉冲之间必定留有零电位的间隙。
(5)差分波形:用相邻码元的电平的跳变和不变来表示消息代码,以电平跳变表示“1”,以电平不变表示“0”。

2、基带传输码的要求
(1)能从其相应的基带信号中获取定时信息;
(2)相应的基带信号无直流成分和只有很少的低频成分;
(3)不受信源统计特性的影响,即能适应于信源的变化;
(4)尽可能地提高传输码型的传输效率;
(5)具有内在的检错能力。
3、基带传输常用码型
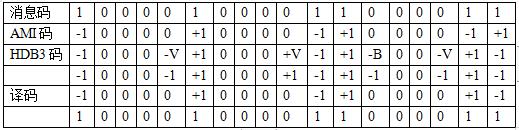
(1)AMI码-传号交替反转码
编码规则:“1” 交替变成“+1” 和“-1” ;“0” 仍保持为“0” 。
消息码 1 1 0 0 1 0 1
AMI码 +1 -1 0 0 +1 0 -1
特点:无直流成分,且只有很少的低频成分,编码简单,提取定时信号困难。
(2)HDB3码-三阶高密度双极性码
编码规则:先检查消息代码中的连0情况,当没有4个或4个以上连0时,按AMI码的编码原则;当有时则将每4个连0小段的第4个0变换成与前一个非0符号同极性的符号。但这可能会破“环极性交替反转”的规律。这个符号被称为破环符号,用V表示(即+1记为+V,-1记为-V)。为使附加V符号后原码仍为无直流分量,还必须保证相邻V符号也极性交替。这一点,当相邻V符号之间有奇数个非0符号时,是能保证的;当有偶数个非0符号时,则不能保证,这时再将该小段的第1个0变换成+B或-B,B符号的极性与前一个非0符号极性相反,并让后面的非0符号从V符号开始在交替变化。
(3)、双相码-曼彻斯特码
编码规则为:每个二进制代码分别用两个具有不同相位的二进制新码去取代的码。0→01;1→10。

(4) 差分双相码(差分曼彻斯特码):
编码方法:不仅与当前的信息有关,而且与前一个信息也有关,也就是说同一个码元的电平有关,即用中央时刻的电平跳变来表示信息。与绝对双相码的不同的是:对于信息1,则前半时间的电平与前一码元的后半时间电平相同,后半时间与本码元前半时间值相反;对信息0,则前半时间的电平与前一码元的后半时间值相反,后半时间值与本码元前半时间值相反。
(5)CMI码-传号反转码
编码规则:“1”码交替用“11”和“00”表示;“0”码用“01”表示。

四、实例演示
1、产生一组单极性不归零码和归零码,并绘制出其时域波形(10个);
(1)程序
方法一:
clear all
M=10; %产生码元数
Ts=1; %每个码元的宽度,即码元的持续时间
L=200; %每码元复制次数
dt=Ts/L;
TotalT=M*Ts; %总时间
wave=round(rand(1,M)); %产生单极性不归零码
% 产生单极性不归零波形
t=0:dt:TotalT-dt;
for i=1:M
if wave(i)==1
for j=1:L
dnrz((i-1)*L+j)=1;
end
else
for j=1:L
dnrz((i-1)*L+j)=0;
end
end
end
subplot(2,1,1)
plot(t,dnrz)
axis([0,TotalT,-0.1,1.1])
%产生单极性归零波形
for i=1:M
if wave(i)==1
for j=1:L/2
drz((2*i-2)*L/2+j)=1;
drz((2*i-1)*L/2+j)=0;
end
else
for j=1:L
drz((i-1)*L+j)=0;
end
end
end
subplot(2,1,2)
plot(t,drz)
axis([0,TotalT,-0.1,1.1])
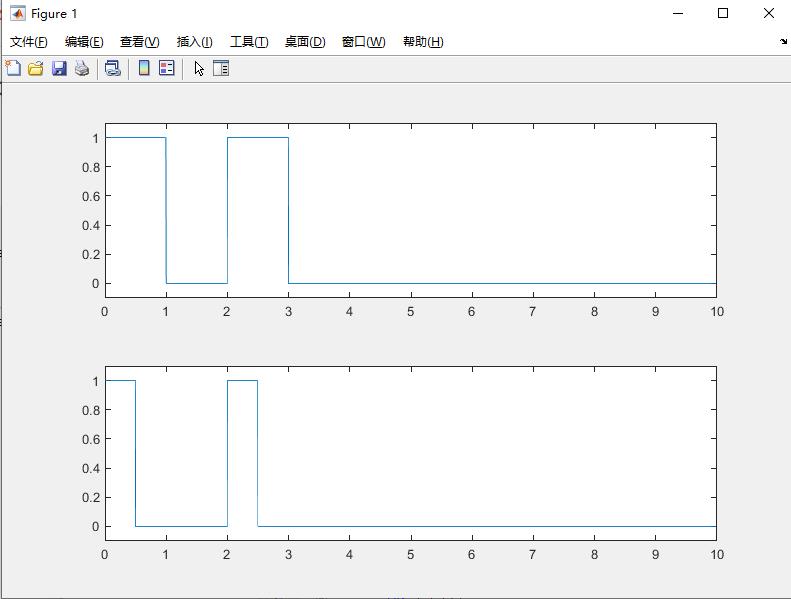
方法二程序如下:
2)单极性不归零码
clear all
M=10; %产生码元数
L=100; %每码元复制L次
Ts=1; %每个码元的宽度,即码元的持续时间
dt=Ts/L; %采样间隔
TotalT=M*Ts; %总时间
t=0:dt:TotalT-dt; %时间
%产生单极性波形
wave=round(rand(1,M)); %产生二进制随机码,M为码元个数
fz=ones(1,L); %定义复制的次数L,L为每码元的采样点数
x1=wave(fz,:); %复制的第1行复制L次
dnrz=reshape(x1,1,L*M); %重排成1行 ,L*M列数组
subplot(2,1,1)
plot(t, dnrz)
axis([0 TotalT -0.1 1.1])
%产生单极性归零波形
N=M*L; %总点数
zkb=0.5; %zkb为占空比
drz=zeros(1,N);
for i=1:zkb*L
drz(i+[0:M-1]*L)=wave;
end
subplot(2,1,2)
plot(t, drz)
axis([0 TotalT -0.1 1.1])

2.双极性码型的部分程序
(1)产生双极性码的函数:
wave=sign(randn(1,M));
(2) 产生双极性不归零波形
snrz=dnrz*2-1; %由单极性不归零波形转换成双极性不归零的波形
(3)产生双极性归零波形
srz=zeros(1,N);
for i=1:zkb*L
srz(i+[0:M-1]*L)=snrz(i+[0:M-1]*L); %由双极性不归零波形转换成双极性归零的波形
end
3.AMI码的时域波形
程序如下:
clear all
M=10; %产生码元数
Ts=1; %每个码元的宽度,即码元的持续时间
L=200; %每码元复制次数
dt=Ts/L;
TotalT=M*Ts; %总时间
t=0:dt:TotalT-dt;
N=M*L; %总点数
wave=round(rand(1,M)); %产生二进制随机码,M为码元个数
% 产生单极性不归零波形
fz=ones(1,L); %定义复制的次数L,L为每码元的采样点数
x1=wave(fz,:); %复制的第1行复制L次
dnrz=reshape(x1,1,L*M); %重排成1*L*M数组
subplot(2,1,1)
plot(t, dnrz)
axis([0 TotalT -0.1 1.1])
amiwave=zeros(1,N);
% 产生AMI码波形
lastcode=1;
for i=0:M-1
if (wave(i+1)==1) %有跳变
if (lastcode==1)
amiwave(i*L+1:i*L+L)=1;
lastcode=-1;
else
amiwave(i*L+1:i*L+L)=-1;
lastcode=1;
end
else
amiwave(i*L+1:i*L+L)=0;
end
end
subplot(2,1,2)
plot(t,amiwave)
axis([0,TotalT,-1.1,1.1])
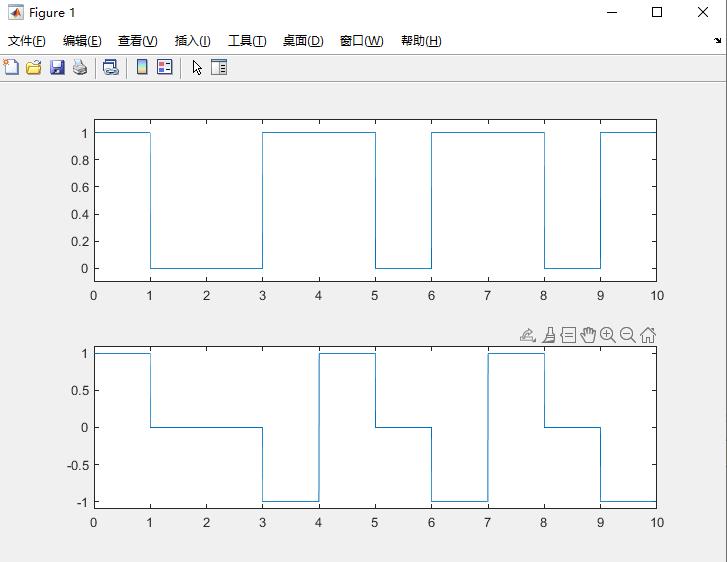
4. HDB3 码的部分程序
hdb3wave=zeros(1,N);
lastcode=1; %上一个1状态
vonevcount=0; %相邻V之间连1数目
zerocount=0; %连零数目
for i=0:M-1 %
if (wave(i+1)==1) %有跳变
zerocount=0;
if (lastcode==1)
hdb3wave(i*L+1:i*L+L)=-1;
lastcode=-1;
vonevcount=vonevcount+1;
else
hdb3wave(i*L+1:i*L+L)=1;
lastcode=1;
vonevcount=vonevcount+1;
end
else
zerocount=zerocount+1;
if (zerocount==4)
if (mod(vonevcount,2)==1) %相邻V之间有奇数个1
if (lastcode==1) %插入000+V
hdb3wave(i*L+1:i*L+L)=1;
else %插入000-V
hdb3wave(i*L+1:i*L+L)=-1;
end
vonevcount=0;
else
if (lastcode==1) %插入-B00-V
hdb3wave((i-3)*L+1:(i-3)*L+L)=-1;
hdb3wave(i*L+1:i*L+L)=-1;
lastcode=-1;
else %插入+B00+V
hdb3wave((i-3)*L+1:(i-3)*L+L)=+1;
hdb3wave(i*L+1:i*L+L)=1;
lastcode=1;
end
vonevcount=0;
end
zerocount=0;
else
hdb3wave(i*L+1:i*L+L)=0;
end
end
end
五、实验内容
1、产生一组双极性码和双极性不归零码,并绘制出其时域波形;
2、产生一组随机数字序列,并绘制该码对应的HDB3码和双相码的时域波形。
以上是关于通信原理实验三 数字基带码型产生实验的主要内容,如果未能解决你的问题,请参考以下文章