带你深入理解 归并排序
Posted 鸢也
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了带你深入理解 归并排序相关的知识,希望对你有一定的参考价值。
归并排序
🎈🎆🎇 前言:
归并排序在八大排序中常考的次数,可以说是名列前茅,地位也是很高的不容疏忽,在排序中快速排序,归并排序和堆排序,面试官基本都会问其中之一的排序,时间复杂度也是在排序中是最快的,所以必须掌握,有了前面快排的知识(快速排序 )和堆排序知识(堆排序),归并理解起来,也不会太抽象
🍕🍔🍟归并排序:
归并排序(Merge Sort)是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
🚗🚓🚕基本思想:
归并排序的思想其实很简单,是采用分治的思想,定义一个mid,从而分开左边和右边,每一次像二叉树一样递归,,让他分成一个一个的数然后最后在合并排序。
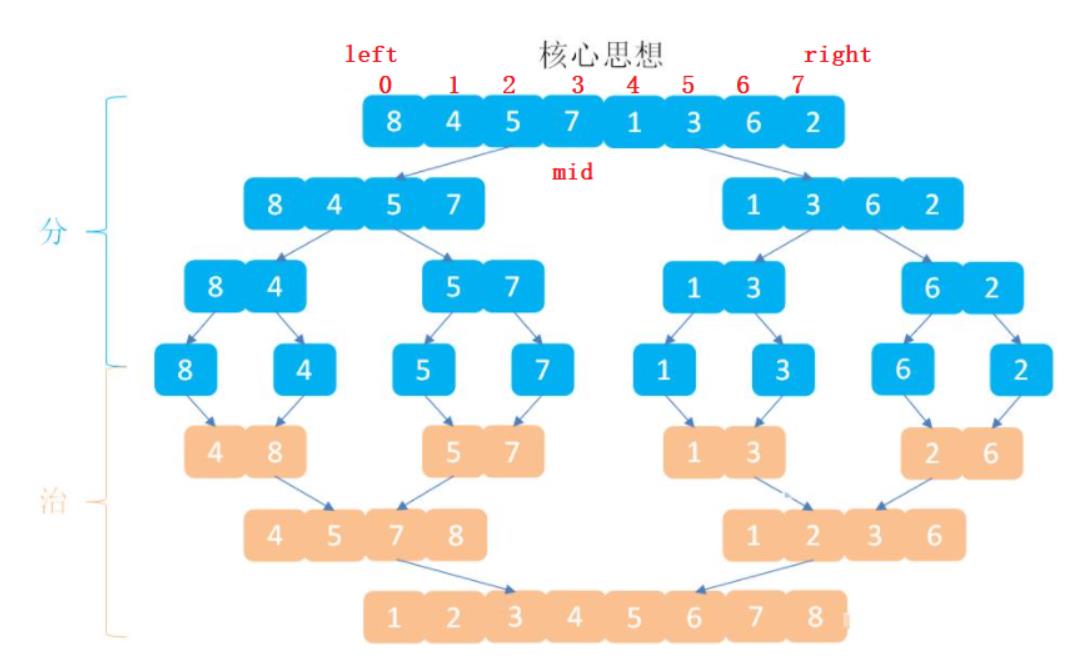
一、合并两个有序数组
要想完成归并排序,首先要知道怎么让两个有序数组合并有序成一个数组,这也是归并排序的核心思想
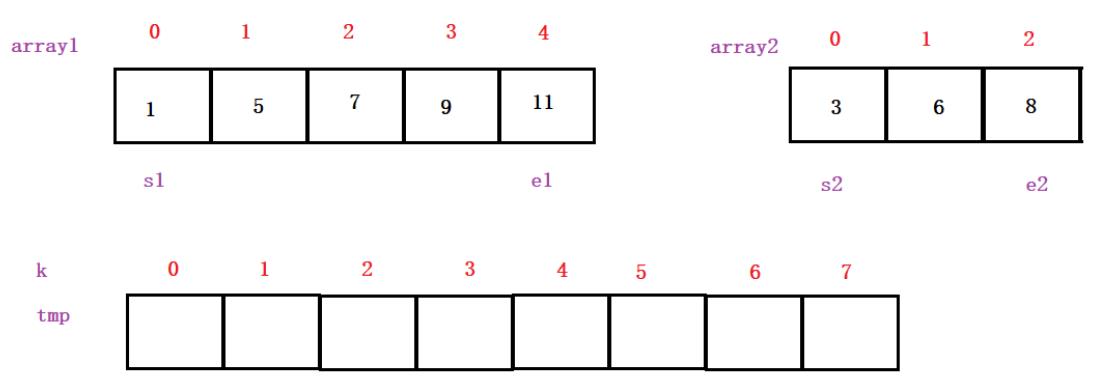
首先有两个有序的数组,定义start和end,两个数组s1和s2进行比较,小的就放进tmp数组中,k是tmp数组的下标(index)。
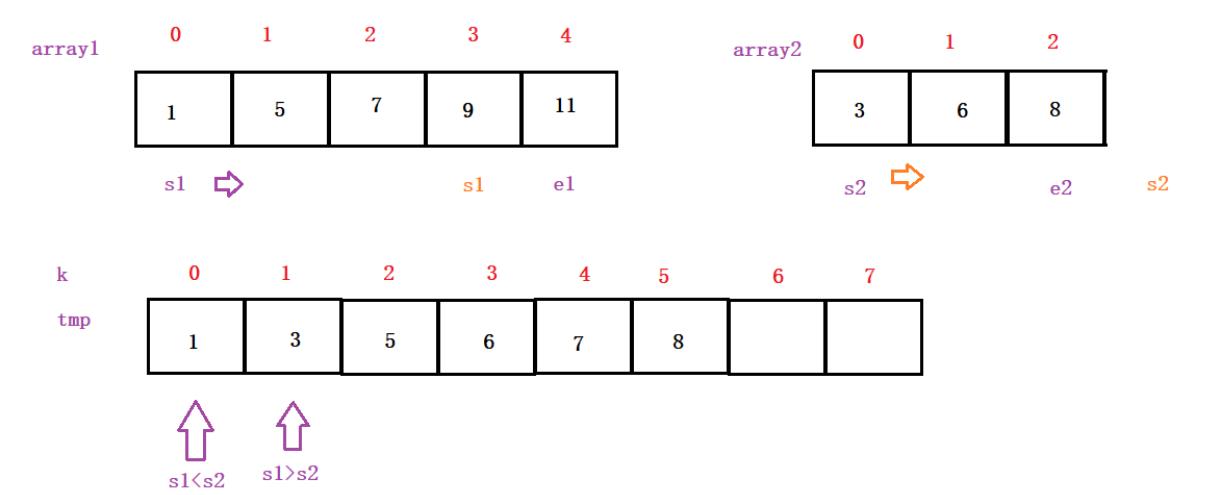
走到这一步了,s2已经走完了,s1剩下的就直接放下去就行了。
🍰🎂🍪核心代码:代码还是很简单的😁😁😁😁
public static int[] mergeArray(int[] array1,int[] array2) {
int[] tmp = new int[array1.length+array2.length];//新数组的长度是array1和array2相加的长度
int k = 0;//tmp数组的下标
int s1 = 0;
int e1 = array1.length-1;//可以不写
int s2 = 0;
int e2 = array2.length-1;//可以不写
//两个数组比较
while (s1 <= e1 && s2 <= e2) {
if(array1[s1] <= array2[s2]) {
tmp[k++] = array1[s1++];
}else {
tmp[k++] = array2[s2++];
}
}
//把剩下的直接放进tmp数组
while (s1 <= e1) {
tmp[k++] = array1[s1++];
}
while (s2 <= e2) {
tmp[k++] = array2[s2++];
}
return tmp;
}
现在我们核心思想代码写完了,那么归并排序就只剩下框架了,这次我们用递归思想;
二、递归版本
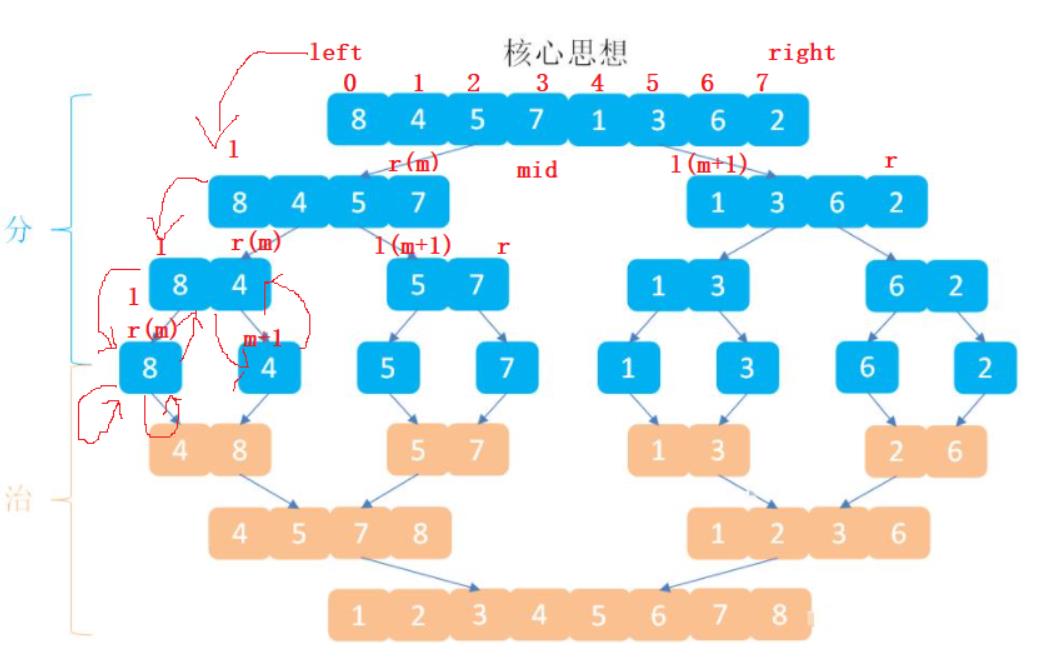
这里要注意的点是分的时候,左边是以mid结尾,右边是mid+1结尾
代码:
//待排序区间
public static void mergeSortInternal(int[] array,int left,int right) {
if(left>=right) {//终止条件
return;
}
int mid=(left+right)/2;
mergeSortInternal(array,left,mid);
mergeSortInternal(array,mid+1,right);
}
上面铺垫的差不多的了,把上面的代码应用起来就可以了,
完整代码:
public static void merge(int[] array,int left,int right,int mid) {
int[] tmp=new int[right=left+1];
int k=0;
//开始分治,mid是左边结尾
int s1=left;
int e1=mid;
//mid+1是右边的开始
int s2=mid+1;
int e2=right;
while (s1<=e1 && s2<=e2) {
if(array[s1]<=array[s2]) {
tmp[k++]=array[s1++];
} else {
tmp[k++]=array[s2++];
}
}
while (s1<=e1) {
tmp[k++]=array[s1++];
}
while (s2<=e2) {
tmp[k++]=array[s2++];
}
for (int i = 0; i < k; i++) {
array[i+left]=tmp[i];//!!!!!!!!
//这里要注意了,不能写成array[i]=tmp[i],因为分右边的时候,是mid+1下标结尾的,
}
}
//待排序区间
public static void mergeSortInternal(int[] array,int left,int right) {
if(left>=right) {//终止条件
return;
}
int mid=(left+right)/2;
mergeSortInternal(array,left,mid);
mergeSortInternal(array,mid+1,right);
merge(array,left,right,mid);
}
public static void mergeSort(int[] array) {
mergeSortInternal(array,0,array.length-1);
}
这里有个要注意的点:
在把tmp里面的数组放进array里面的数组时,一定要写成 array[i+left]=tmp[i];
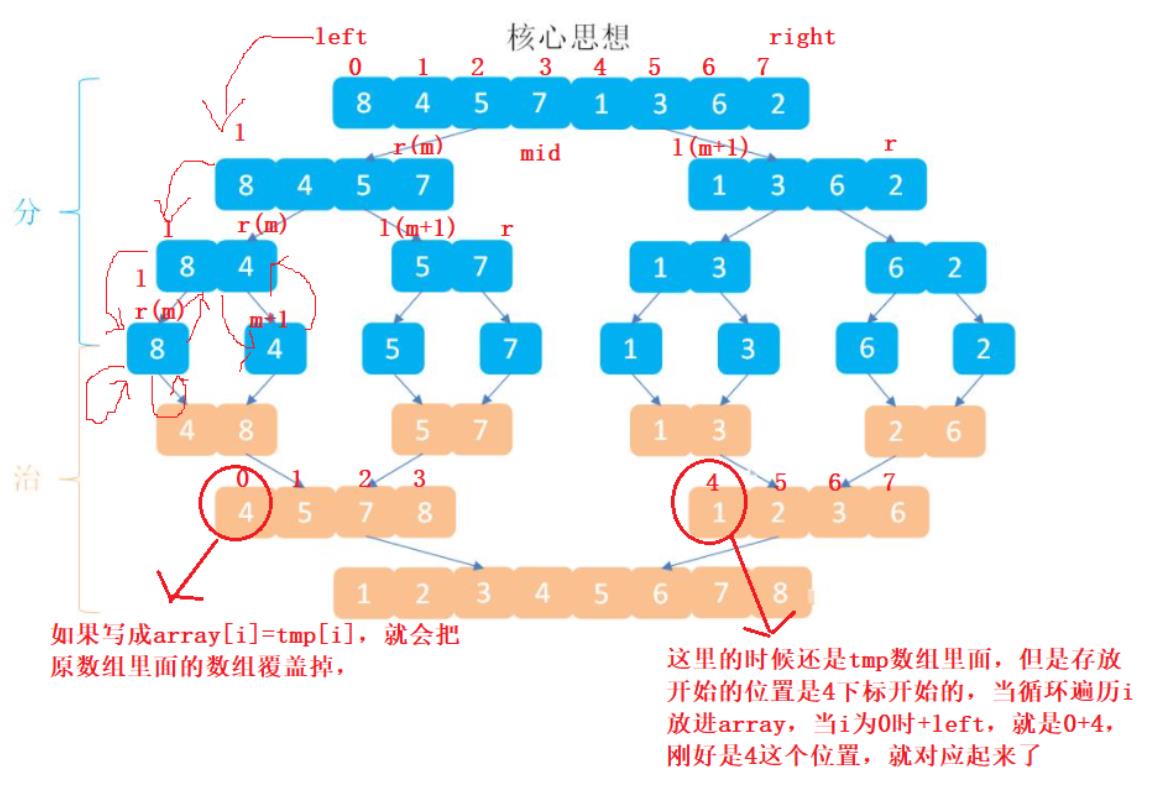
如果写成array[i]=tmp[i],就会把原数组里面的数组覆盖掉,
三、性能分析
| 时间复杂度 | 空间复杂度 |
|---|---|
| O(n * log(n)) | O(n) |
时间复杂度相当于二叉树高度+遍历,空间复杂度因为有new tmp所以是O(n).
四、非递归版本
非递归版本理解起来就麻烦了,因为会考虑很多种情况,还要注意很多边界的问题,实属心烦,如果要写归并排序还是直接写递归的好,如果有要求那就,只能硬着头皮干了🐱👤🐱👤🐱👤🐱👤🐱👤🐱👤🐱👤🐱👤🐱👤🐱👤
首先要归并是必须要两个数组的,但是每个数组会分gap,先是1组,然后2组,然后4组,跟上面图差不多的分组。

😎🙂🤗分组代码:
public static void mergeSort(int[] array) {
for (int gap = 1; gap < array.length; gap*=2) {
merge2(array,gap);
}
}
由图所示,这样就可以确定 s1,e1,s2,e2的位置了,但是e2可能要稍微注意:

所以当e2大于数组长度的时候,直接len-1,
😶😑😐位置代码:
public static void merge2(int[] array,int gap) {
int[] tmp = new int[array.length];
int k = 0;
int s1 = 0;
int e1 = s1+gap-1;
int s2 = e1+1;
int e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
}
下面就是两个数组的比较了,两个数组就必须有两个段,所以会有一个判断条件两数组比较也写过直接拿来用
代码:
while (s2 < array.length) {//这是判断必须有两个段的判断条件
while (s1 <= e1 && s2 <= e2) {
if (array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
while ( s1 <= e1 ) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
}
因为不是递归,所以两段数组比完了,还要确定下一次两段数组的位置所以就要接着写:
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
但是写了上面的代码会发生几种情况:
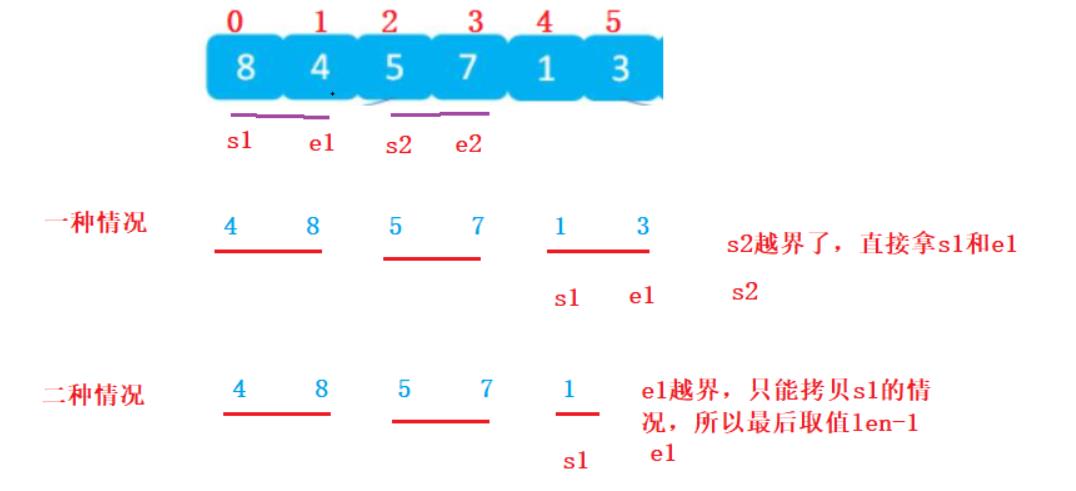
会出现以上两种情况,最后把多余的移下去,归根结底,最后的取值范围就是len-1;
完整代码:
public static void merge2(int[] array,int gap) {
int[] tmp = new int[array.length];
int k = 0;
int s1 = 0;
int e1 = s1+gap-1;
int s2 = e1+1;
int e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
//一定要有2个段 ,拿s2判断
while (s2 < array.length) {
while (s1 <= e1 && s2 <= e2) {
if (array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
while ( s1 <= e1 ) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
}
//只剩下最后段了,综合考虑会出现多重情况,归根结底取值范围就是len-1
while (s1 <= array.length-1) {
//s1 <= e1还要考虑的情况是 存在s1但是不存在e1情况下, s1 <= array.length-1
tmp[k++] = array[s1++];
}
for (int i = 0; i < k; i++) {
array[i] = tmp[i];
}
}
public static void mergeSort1(int[] array) {
for (int gap = 1; gap < array.length; gap*=2) {
merge2(array,gap);
}
}
以上就是这篇帖子的全部内容了,必须全掌握,在七大排序中,快排,堆排和归并都是常考的内容,快排出现的次数最多的,其次就是堆和归并,再后就是直接插入,希尔,选择,冒泡 ,这些相对来说代码和思想要简单点,希尔排序有点难理解,但是几乎不考,主要还是要熟知他们的时间复杂度,空间复杂度,稳定些,还有他们的主要实现都要掌握, 总结了归并排序的代码, 若想看全代码可以 点击我的 Github ,里面都是整理的代码。
铁汁们,觉得笔者写的不错的可以点个赞哟❤🧡💛💚💙💜🤎🖤🤍💟,收藏关注呗,你们支持就是我写博客最大的动力

以上是关于带你深入理解 归并排序的主要内容,如果未能解决你的问题,请参考以下文章